浅谈淀粉质

题意：给定一棵带权无根树，问是否有点对的距离为k

暴力的做法可以枚举所有点对，树上差分即可，复杂度为\(O(n^2logn)\)，显然还需要优化

有一个显然的性质，对于任意两个点所夹成的路径，有两种情况：

\(1.\)经过根节点的路径

\(2.\)不经过根节点的路径

对与第一类路径，\(dis[u->v] = dis[u->rt] + dis[v ->rt]\)

对于第二类路径，我们可以求出LCA在进行讨论，但是我们可以继续递归下去，找到另一个rt，把他转化成第一类路径来讨论

不难发现，这样递归下去的复杂度是和深度有关的，所以我们要尽量的减小深度来优化复杂度，那么我们怎么办呢？

对于每一棵树，我们都有一个重心（删掉重心后剩下的子树尽可能地平衡（分出来的最大子树的\(size\)尽可能地小））

举个例子，对于这张图，深度达到了6，显然不够优秀

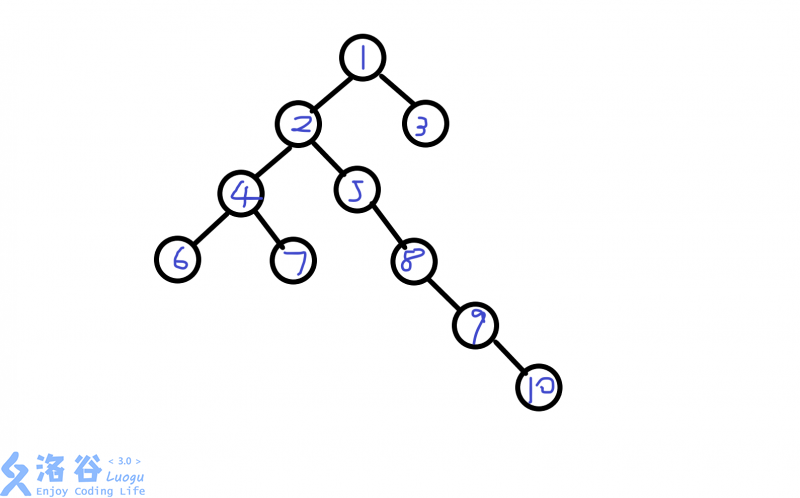
但是如果我们以5为根，树就会变成这样，深度变为了4：

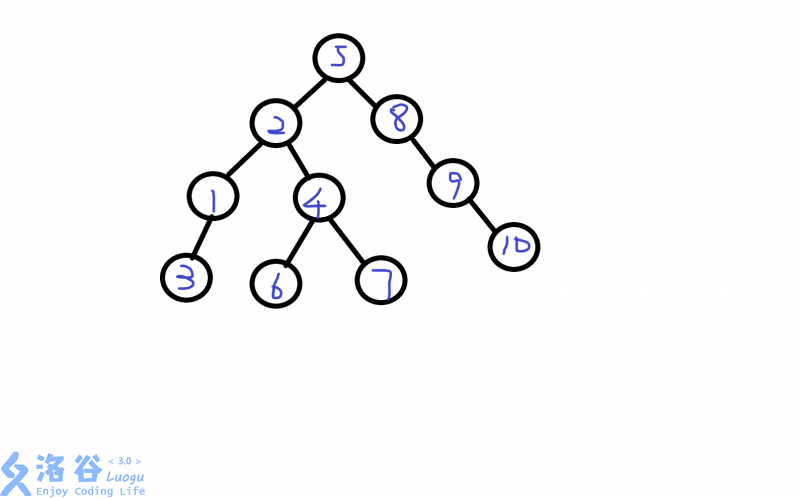
可见根的选择是对复杂度有影响的，如果数据足够大，出题人足够毒瘤，那么影响显然还会更大

那重心要怎么着呢？我们可以利用树（mo）形（ni）DP的思想来做，即找到该节点所有的子树，找到最大的哪一棵即可，代码如下：

il void getroot(int u, int fr)
{
	dp[u] = 0, size[u] = 1;
	Next(i, u)
	{
		int v = e[i].v;
		if(v == fr || vis[v]) continue;
		getroot(v, u);
		size[u] += size[v];
		dp[u] = max(dp[u], size[v]);
	}
	dp[u] = max(dp[u], sum - size[u]);//还有一棵以其父亲节点为根的子树
	if(dp[u] < dp[root]) root = u;
}

找到重心后，我们不断的递归，在递归过程中也要不断寻找重心来优化复杂度。

代码如下：

il void solve(int u)
{
	vis[u] = pd[0] = 1, doit(u);//doit表示做一些
	Next(i, u)
	{
		int v = e[i].v;
		if(vis[v]) continue;
		dp[0] = n, sum = size[v], root = 0;
		getroot(v, u), solve(root);
	}
}

那么doit要怎么写呢？

由于我们保证了所有的树都是第一种树（经过根节点的路径），所以我们对于每一个根，可以先预处理出每一个子节点到根的距离，这样我们就可以得到对于每一个点可能出现的距离

代码如下：

il void getdis(int u, int fr)
{
	rev[++ tot] = dis[u];
	Next(i, u)
	{
		int v = e[i].v;
		if(v == fr || vis[v]) continue;
		dis[v] = dis[u] + e[i].w;
		getdis(v, u);
	}
}

求出了所有距离以后，我们就可以合并答案了，把任意两个出现的距离凑在一起，并判断可否凑出我们需要的k即可（注意复原的时候不要用memset，不然复杂度就是\(O(n^2)\)了）

il void doit(int u)
{
	int c = 0;
	Next(i, u)
	{
		int v = e[i].v;
		if(vis[v]) continue;
		tot = 0, dis[v] = e[i].w, getdis(v, u);
		rep(j, 1, tot) rep(k, 1, m) if(query[k] >= rev[j]) pax[k] |= pd[query[k] - rev[j]];
		rep(j, 1, tot) q[++ c] = rev[j], pd[rev[j]] = 1;
	}
	rep(i, 1, c) pd[q[i]] = 0;
}

所有代码如下：

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define re register
#define debug printf("Now is Line : %d\n",__LINE__)
#define file(a) freopen(#a".in","r",stdin);freopen(#a".out","w",stdout)
//#define int long long
#define inf 123456789
#define mod 1000000007
il int read()
{
    re int x = 0, f = 1; re char c = getchar();
    while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
#define rep(i, s, t) for(re int i = s; i <= t; ++ i)
#define drep(i, s, t) for(re int i = t; i >= s; -- i)
#define Next(i, u) for(re int i = head[u]; i; i = e[i].next)
#define lb(x) (x)&(-(x))
#define ls k * 2
#define rs k * 2 + 1
#define _ 10005
#define ___ 10000005
#define __ 105
struct edge{int v, next, w;}e[_ << 1];
int n, m, head[_], cnt, dp[_], tot, size[_], sum, root;
int dis[_], vis[_], pd[___], rev[_], pax[__], q[_], query[__];
il void add(int u, int v, int w){e[++ cnt] = (edge){v, head[u], w}, head[u] = cnt;}
il void getroot(int u, int fr)
{
	dp[u] = 0, size[u] = 1;
	Next(i, u)
	{
		int v = e[i].v;
		if(v == fr || vis[v]) continue;
		getroot(v, u);
		size[u] += size[v];
		dp[u] = max(dp[u], size[v]);
	}
	dp[u] = max(dp[u], sum - size[u]);
	if(dp[u] < dp[root]) root = u;
}
il void getdis(int u, int fr)
{
	rev[++ tot] = dis[u];
	Next(i, u)
	{
		int v = e[i].v;
		if(v == fr || vis[v]) continue;
		dis[v] = dis[u] + e[i].w;
		getdis(v, u);
	}
}
il void doit(int u)
{
	int c = 0;
	Next(i, u)
	{
		int v = e[i].v;
		if(vis[v]) continue;
		tot = 0, dis[v] = e[i].w, getdis(v, u);
		rep(j, 1, tot) rep(k, 1, m) if(query[k] >= rev[j]) pax[k] |= pd[query[k] - rev[j]];
		rep(j, 1, tot) q[++ c] = rev[j], pd[rev[j]] = 1;
	}
	rep(i, 1, c) pd[q[i]] = 0;
}
il void solve(int u)
{
	vis[u] = pd[0] = 1, doit(u);
	Next(i, u)
	{
		int v = e[i].v;
		if(vis[v]) continue;
		dp[0] = n, sum = size[v], root = 0;
		getroot(v, u), solve(root);
	}
}
int main()
{
	file(a);
	dp[0] = sum = n = read(), m = read();
	rep(i, 1, n - 1) {int u = read(), v = read(), w = read(); add(u, v, w), add(v, u, w);}
	rep(i, 1, m) query[i] = read();
	getroot(1, 0), solve(root);
	rep(i, 1, m) puts(pax[i] ? "AYE" : "NAY");
	return 0;
}