3.5tensorflow线性回归和线性拟合

自己开发了一个股票智能分析软件，功能很强大，需要的点击下面的链接获取：

https://www.cnblogs.com/bclshuai/p/11380657.html

1.1  tensorflow线性回归

以线性回归为例，以梯度下降法计算线程方程的参数，通过多次学习和迭代计算出参数。如果采用numpy等常规的科学计算法库去实现，需要人工求出函数的偏导数，并且需要根据求导结果更新参数。如果采用tensorflow框架，可以自动求导和更新参数。

1.1.1         变量归一化

归一化定义

由于实际求解往往使用迭代算法，如果目标函数的形状太“扁”，即变量之间的数量级相差太大，迭代算法可能收敛得很慢甚至不收敛。所以对于具有伸缩不变性的模型，最好也进行数据标准化，即归一化让数值在同一个数量级内。

归一化优点

（1）提升模型的收敛速度，变量数量级相差大，成椭圆形梯度下降，走之路线，收敛速度慢，数量级相同，成圆形梯度下降，垂直于圆心迭代，所以收敛速度快。

 

 

 

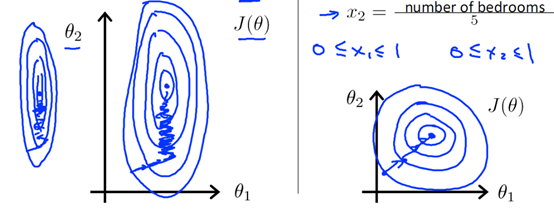
（2）提高模型的精度，数量级相差太大，波动对结果的影响大，造成精度损失。

归一化方法

线性归一化，线性归一化会把输入数据都转换到[0 1]的范围，公式如下

 

1.1.2         reduce_sum、reduce_mean、reduce_max、reducemin函数介绍

reduce_sum函数是用来求多维tensor的元素之和的方法，reduce是降维的意思，sum是求和的意思。其定义如下：

reduce_sum(input_tensor, axis=None, keepdims=False, name=None)

input_tensor：输入求和的张量

axis：降维的维度，比如2行3列的矩阵，维度是（0,1）0表示行，1表示列。axis等于0时，2行3列变成1行3列；axis=1时，2行3列默认变为1行两列，只有在keepdims ，才是2行1列。

keepdims：是否保持维度，如果为True，axis=1时，2行3列变为2行1列

实例

import tensorflow as tf
import numpy as np
x = tf.constant([[1, 1, 1], [1, 1, 1]])
print(x)
y1=tf.reduce_max(x);
print(y1)#不指定axis时，等于所有元素相加1+1+1+1+1+1+1=6
y2=tf.reduce_max(x,0)
print(y2)#指定按行降维，变成一行3列，每列元素相加[2,2,2]
y3=tf.reduce_max(x,1)
print(y3)#指定按列降维，每行元素相加，因为keepdims默认为false，输出1行2列[3,3]
y4=tf.reduce_max(x,1,True)
print(y4)#指定按列降维，每行元素相加，同时保持维度，输出2行1列[[3],[3]]

 

 

输出

tf.Tensor(

[[1 1 1]

 [1 1 1]], shape=(2, 3), dtype=int32)

tf.Tensor(6, shape=(), dtype=int32)

tf.Tensor([2 2 2], shape=(3,), dtype=int32)

tf.Tensor([3 3], shape=(2,), dtype=int32)

tf.Tensor(

[[3]

 [3]], shape=(2, 1), dtype=int32)

 

同理reduce_mean是求平均值，参数含义相同

reduce_mean(input_tensor, axis=None, keepdims=False, name=None)

reduce_max求最大值，参数含义相同

reduce_max(input_tensor, axis=None, keepdims=False, name=None):

reduce_min求最小值，参数含义相同

1.1.3         numpy和tensorflow线程回归对比

线性回归是给出线程方程y=ax+b，给出损失函数误差平方和

 

 

然后将损失函数对参数a，b求导数，得到偏导数，偏导数乘以学习率，对参数a，b进行迭代计算。

实例代码

使用numpy需要手动计算偏导数，并更新参数，对于一些复杂的函数，很难求出导数，这时就要使用tensorflow 来自动求导数。

某城市的房价和年份的数据如下，求出线性参数y=ax+b

年份x	2013	2014	2015	2016	2017
价格y	12000	14000	15000	16500	17500

因为年份和价格数据量级不同，所以需要进行归一化，将数据范围控制在0,1之间。通过减去最小值再除以区间值的方式得到归一化之后的数据，再进行线性回归。

（1）   使用numpy手动求导线性回归

实例代码如下

import numpy as np
import matplotlib.pyplot as plot
x_raw=np.array([2013,2014,2015,2016,2017],dtype=np.float)
y_raw=np.array([12000,14000,15000,16500,17500],dtype=np.float)
#归一化
x=(x_raw-x_raw.min())/(x_raw.max()-x_raw.min())
y=(y_raw-y_raw.min())/(y_raw.max()-y_raw.min())
print(x)#[0.   0.25 0.5  0.75 1.  ]
print(y)#[0.         0.36363636 0.54545455 0.81818182 1.        ]
a,b=0.0,0.0#初始值
num=10000#迭代次数
learnrate=0.001#学习率
for e in range(num):#循环迭代
    y_predit=a*x+b
    grad_a,grad_b=(y_predit-y).dot(x),2*(y_predit-y).sum()
    a,b=a-learnrate*grad_a,b-learnrate*grad_b
print(a,b)#0.9784232246514815 0.05634210319697519
ytest=a*x+b
print(ytest)#[0.0563421  0.30094791 0.54555372 0.79015952 1.03476533]
plot.scatter(x,y,c='r')
plot.plot(x,ytest,c='b')
plot.show()

 

输出结果图像如下

 

 

 

（2）   使用tensorflow自动求导线性回归

实例代码如下

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plot
x_raw=np.array([2013,2014,2015,2016,2017],dtype=np.float)
y_raw=np.array([12000,14000,15000,16500,17500],dtype=np.float)
#归一化
x=(x_raw-x_raw.min())/(x_raw.max()-x_raw.min())
y=(y_raw-y_raw.min())/(y_raw.max()-y_raw.min())
#转化为tensorflow的张量
x=tf.constant(x,dtype=tf.float32)#指定float32，否则会变成float64报错
y=tf.constant(y,dtype=tf.float32)
print(x)#tf.Tensor([0.   0.25 0.5  0.75 1.  ], shape=(5,), dtype=float32)
print(y)#tf.Tensor([0.  0.36363637 0.54545456 0.8181818  1.], shape=(5,), dtype=float32)
#初始化变量
a,b=tf.Variable(initial_value=0.),tf.Variable(initial_value=0.)
#组成变量数组
variables=[a, b]
#循环次数
num=10000
#迭代算法
optimizer=tf.keras.optimizers.SGD(learning_rate=1e-3)
#循环
for e in range(num):
    with tf.GradientTape() as tape:
        #预测函数
        y_pred=a*x+b
        #损失函数
        loss=tf.reduce_sum(tf.square(y_pred-y))
        #对变量求导
    grads=tape.gradient(loss, variables)
        #调整参数
    optimizer.apply_gradients(grads_and_vars=zip(grads,variables))
print(a,b)#<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.9817748> <tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.0545703>
ytest=a*x+b
print(ytest)#tf.Tensor([0.0545703 0.300014  0.5454577 0.7909014 1.0363451], shape=(5,), dtype=float32)
plot.scatter(x,y,c='r')
plot.plot(x,ytest,c='b')
plot.show()

 

输出的图像结果如下：

 

 

 

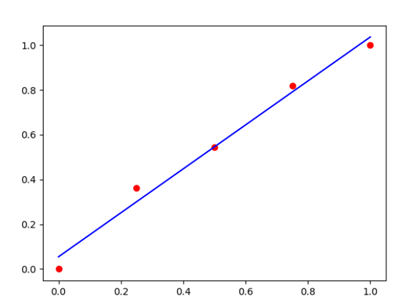
通过对比可以知道，输出的结果完全一致。

（3）   使用tensorflow自动求导线性拟合

构造线性的离散点y=0.3x+0.7+np.random.normal(0.0,0.1)，然后用线性回归去拟合这些离散的点求得参数看是否接近0.3和0.7。

代码如下

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plot
#定义数据数量
num=100
xdata=[]
ydata=[]
#生成数据
xdata=np.linspace(-1.,1.,100)#线性等分生成100个数据
#生成线性数据a=0.3,b=0.7，加上随机噪声
ydata=[0.3*v+0.7+np.random.normal(0.0,0.1) for v in xdata]
#定义变量
a=tf.Variable(initial_value=0.,dtype=tf.float32)
b=tf.Variable(initial_value=0.,dtype=tf.float32)
variables=[a, b]
#声明梯度下降优化算法
optimizer = tf.keras.optimizers.SGD(learning_rate=2e-3)
#声明循环迭代次数
num=1000
#进行迭代，更新参数
for s in range(num):
    with tf.GradientTape() as tape:
        #预测值
        y_pred=a*xdata+b
        #损失函数
        loss=tf.reduce_sum(tf.square(y_pred-ydata))
        #计算梯度
        grads=tape.gradient(loss,variables)
        #更新参数
        optimizer.apply_gradients(grads_and_vars=zip(grads,variables))
        #每隔100次输出一次结果
        if s%100==0:
            print("step: %i, loss: %f, a: %f, b: %f" % (s, loss, a.numpy(), b.numpy()))

print(a.numpy(),b.numpy())
plot.scatter(xdata,ydata,c='r')
plot.plot(xdata,a*xdata+b,c='b')
plot.show()

 

输出结果如下，每隔100次迭代输出一次一次结果，大家可以看到经过100迭代之后，参数就已经收敛，不在变化。输出结果也非常接近实际值。

step: 0, loss: 50.548035, a: 0.040768, b: 0.273359

step: 100, loss: 0.790290, a: 0.299707, b: 0.683397

step: 200, loss: 0.790290, a: 0.299707, b: 0.683397

step: 300, loss: 0.790290, a: 0.299707, b: 0.683397

step: 400, loss: 0.790290, a: 0.299707, b: 0.683397

step: 500, loss: 0.790290, a: 0.299707, b: 0.683397

step: 600, loss: 0.790290, a: 0.299707, b: 0.683397

step: 700, loss: 0.790290, a: 0.299707, b: 0.683397

step: 800, loss: 0.790290, a: 0.299707, b: 0.683397

step: 900, loss: 0.790290, a: 0.299707, b: 0.683397

0.29970676 0.68339676

 

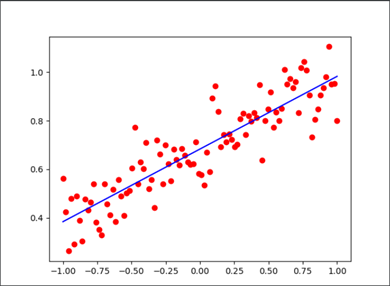
用matlabplot画出图片如下所示