n的阶乘分解成素数幂的积

题目描述：

 

题目分析：对于某个阶乘，每个乘积因子总能被一些有小到大的素数除至1，，总体上表现为某个阶乘总能由一些由小到大的素数的幂的积表示。这样我们的目的就到到了

代码展示：

//阶乘素数分解
#include<stdio.h>
#include<string.h>
int prime[100],p[100];

int is_prime(int x)
{
    int sign=1;
    for(int i=2;i*i<x;i++)
    {
        if(x%i==0)
        {
            sign=0;
            break;
        }
    }
    if(sign) return 1;
    else return 0;
}

int main()
{
    int count=0,n;
    for(int i=2;i<=100;i++)
    {
        if(is_prime(i)) prime[count++]=i;
    }
    while(scanf("%d",&n)==1)
    {
        int max=0;
        memset(p,0,sizeof(p));       //这一步必不可少，不然会出错
        printf("%d!=(",n);
        for(int i=1;i<=n;i++)        //对于阶乘里出现的每个数，都能被某些从小到的的素数整除，变成1后不再管
        {
            for(int j=0;j<count;j++)
            {
                int m=i;
                while(m%prime[j]==0)
                {
                    p[j]++;
                    m=m/prime[j];
                    if(j>max) max=j;
                }
            }
        }
        for(i=0;i<max;i++) printf(" %d",p[i]);
        printf(")\n");
    }
    return 0;
}

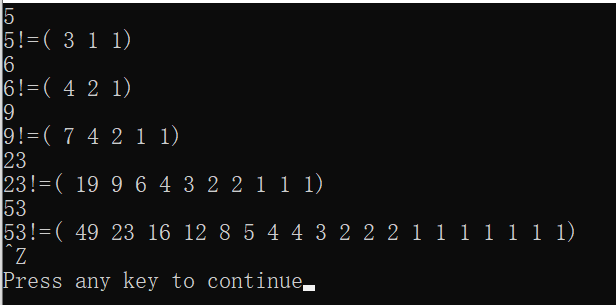
运行结果（这里多了括弧）：