树与堆——认爹之旅

前言

马上开学了啊，希望开学考能有一个好成绩！

一、树

（一）基本的树

树是由 \(n(n \ge 0)\) 个节点，和 \(n-1\) 条边构成的集合。在树中，任何两个节点间有且仅有一条路径。

这是一棵树：

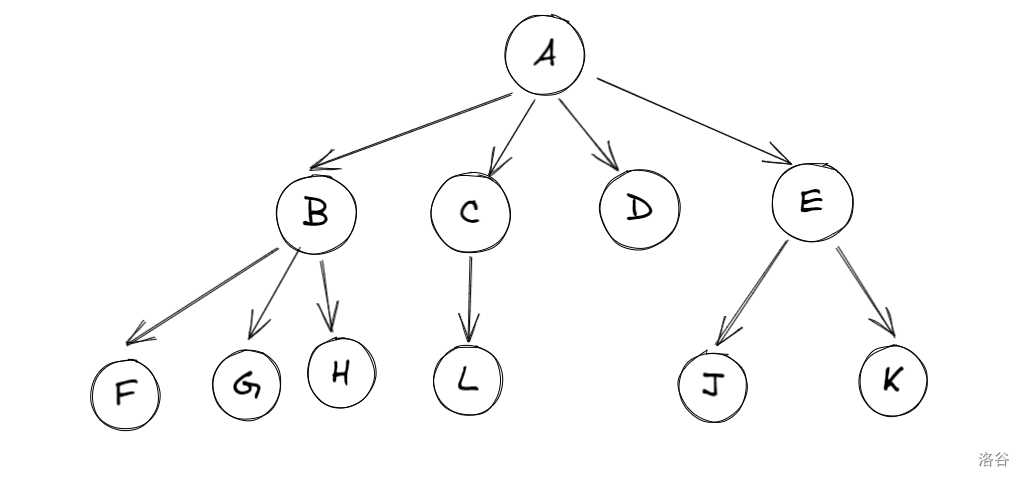
以下是概念大全：

• 空树：没有任何节点；
  非空树：至少有一个节点。
  子树：除根外的所有节点可以分为多个互不相交的集合，每个集合都可以看作一棵树。
• 节点：数中的元素。
  节点的度：拥有子树的数目称为该节点的度。
• 父亲：该节点的上层节点；
  兄弟：拥有同一个父亲的其他节点；
  孩子：该节点的下层节点。
  祖先：从该节点到根节点路径之中的所有节点。
  子孙：以该节点为根的子树中的所有节点
• 根：没有父亲的节点，一个树只有一个根节点。
  叶：度为 \(0\) 的节点。

（二）二叉树

1.概念及其储存

每个节点最多只有两个子节点的树称为二叉树。

一些特性：

• 第 \(i\) 层上最多有 \(2^{i-1}\) 个节点。
• 高度为 \(h\) 的二叉树最多有 \(2^{h-1}\) 个节点。
• 在非空二叉树中，叶结点个数为 \(x\)，度为 \(2\) 的节点数为 \(y\) 则有：\(x=y+1\)

二叉树有两种特殊情况：满二叉树和完全二叉树

满二叉树：每层节点数都达到最大的二叉树。

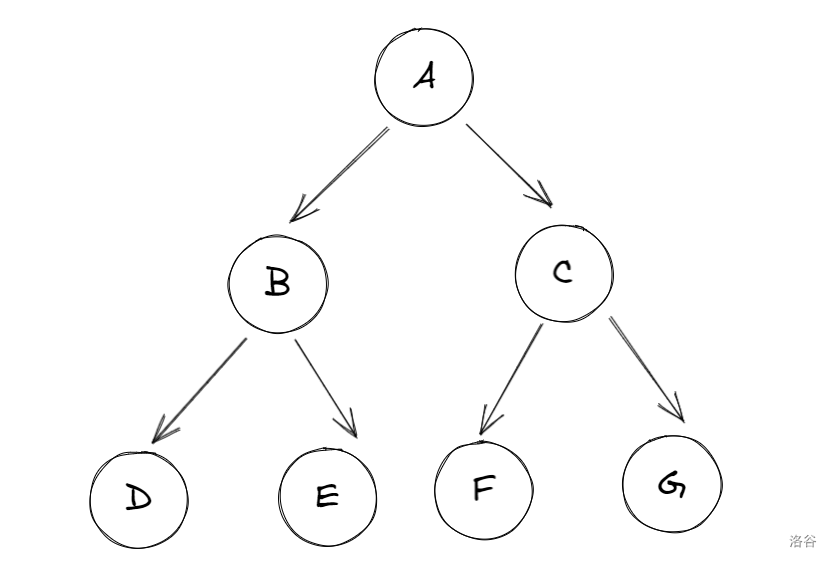
完全二叉树满足两个条件：

• 除底层外，其余各层节点都达到最大值；
• 底层节点集中在左侧连续位置上。
  

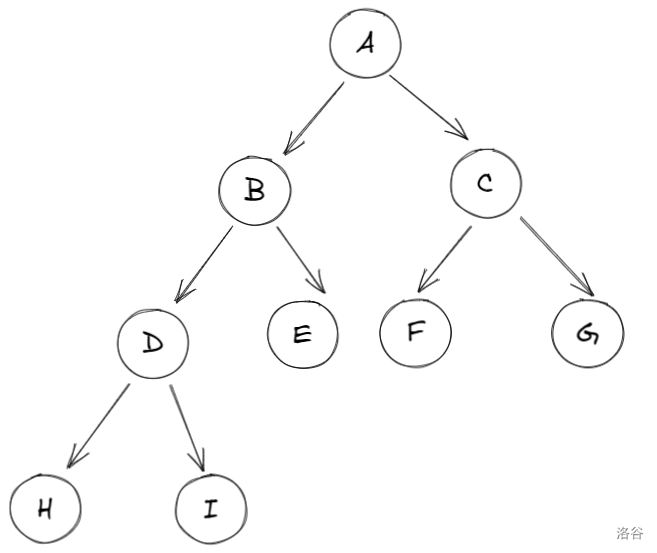
如何用代码实现储存二叉树？

看：

struct bbd{
    int data;//名称
    int left;//左子节点
    int right;//右子节点
    int father;//父节点
}p[10005];

2.二叉树的遍历

以下是二叉树的常见遍历方法：

• 层次遍历
• 递归遍历
  • 前序遍历
  • 中序遍历
  • 后序遍历

以下图为例讲一讲这几种遍历方法：

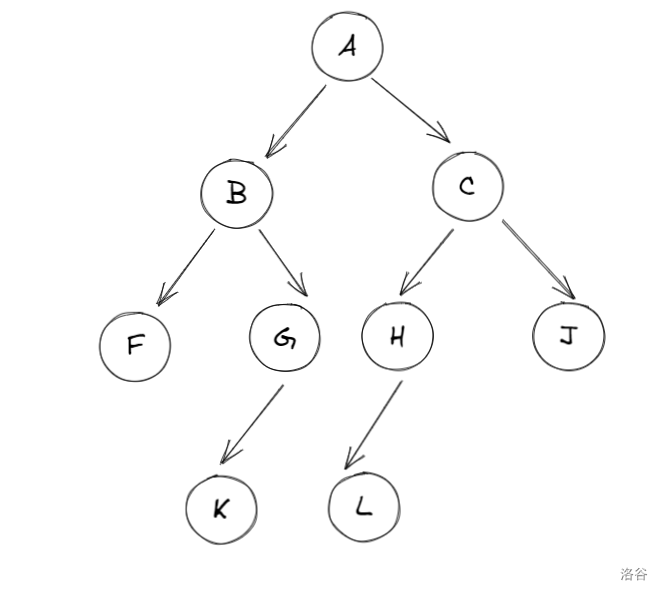
层次遍历

层次遍历很好理解，就是从上到下沿着二叉树的每一层进行遍历，适合人工计算时使用。

对于上图，层次遍历为：\(A-B-C-F-G-H-J-K-L\)。

递归遍历

递归遍历适合计算机使用，有着较强的关联性和逻辑性。
递归遍历分 \(3\) 种：

• 前序遍历
  先访问根节点，再访问左子树，再访问右子树。
  对于上图，前序遍历为：\(A-B-F-G-K-C-H-L-J\)。
• 中序遍历
  先访问左子树，再访问根节点，再访问右子树。
  对于上图，中序排列为：\(F-B-K-G-A-L-H-C-J\)。
• 后序遍历
  先访问左子树，再访问右子树，最后访问根节点。
  对于上图，后序排列为：\(F-K-G-B-L-H-J-C-A\)。

程序实现

程序时限分为两个重要板块：初始化和递归输出。

初始化很简单，弄清顺序就行：

void qian(int t){
    if(t>0){
	printf("%d ",p[t].data);//根
	qian(p[t].left);//左
	qian(p[t].right);//右
    }
}
void zhong(int t){
    if(t>0){
	zhong(p[t].left);//左
	printf("%d ",p[t].data);//根
	hong(p[t].right);//右
    }
}
void hou(int t){
    if(t>0){
	hou(p[t].left);//左
	hou(p[t].right);//右
	printf("%d ",p[t].data);//根
    }
}

（注：这里面的 \(t\) 调用时为根节点所在位置）

如何进行初始化呢？
前面我们讲到的结构体储存派上用场了，对于输入的 \(a\) 和 \(b\)，我们知道：

• bbd[b].data=b；
  bbd[b].father=a。
• bbd[a].data=a;
  bbd[a].left=b或bbd[a].right=b。

如何判断 \(b\) 是 \(a\) 的左子节点还是右子节点呢？
很简单，判断 \(a\) 的左子节点数值是否为空即可。

还有一个问题：\(t\) 怎么求？
前面不是说过根节点的性质么？没有父节点，利用此性质在结构体数组里面搜一遍就知道根节点所在数组位置了。

就像这样：

for(int i=1;i<n;i++){
    scanf("%d%d",&a,&b);
		
    p[a].data=a;
    if(p[a].left==0) p[a].left=b;
    else p[a].right=b;
		
    p[b].data=b;
    p[b].father=a;
}
int basic;
for(int i=1;i<=n;i++){
    if(p[i].father==0) basic=i;
}

拓展

前面是我们通过一颗树去生成前序、中序、后序遍历，那现在我们反过来：给你前序、中序或后序，你能把树还原么？

这样还原在编程里叫做：建树（你可以理解为：建好一颗树，你就能有所建树）。

看题：

给出两个由大写字母构成的字符串（长度不超过 \(26\)），一个表示二叉树的前序遍历序列，一个表示二叉树的中序遍历序列，请你计算出该二叉树的后序遍历序列。

你也可以在这里找到题目：P1827。

如何思考这一道题？

前序遍历特点：第一个位置的数永远是该二叉树（或子二叉树）的根。
中序遍历特点：二叉树（或子二叉树）的根会把遍历序列分成两部分。

那么，我们枚举每一个根的顺序，就可以模拟出后序遍历的结果。

用字母太抽象，我们用数字来模拟一组数据：
\(X=\mathbf{1234567},Y=\mathbf{4352617}\)。

首先，\(A\) 的第一位是 \(1\)，我们在 \(B\) 中找到 \(1\)：
\(X=\mathbf{[1]234567},Y=\mathbf{43526[1]7}\)。

根据上面所说的性质，可以得到：\(\mathbf{43526}\) 位于以 \(1\) 为根的左子树中，而 \(\mathbf{7}\) 位于以 \(1\) 为根的右子树中。

由于前序遍历的左子树、右子树一定会报团取暖（不会相交），所以从前序遍历中提取出 \(\mathbf{23456}\) 作为新的前序遍历串，与中序遍历中的 \(\mathbf{43526}\) 进行一个新的查找，递归求解。

• 以字母为节点值：

#include<bits/stdc++.h>
using namespace std;
int len;
string a,b;
void bbd(int n,string a,string b){
    if(n<=0){
	return;
    }
    int w=b.find(a[0]);
    bbd(w,a.substr(1,w),b.substr(0,w));
    bbd(n-w-1,a.substr(w+1,n-w),b.substr(w+1,n-w));
    printf("%c",a[0]);
}
int main() {
    cin>>a>>b;
    len=a.length();
    bbd(len,a,b);
    return 0;
}

• 以数字为节点值

#include<bits/stdc++.h>
using namespace std;
int n;
int a[1000005];
int b[1000005];
int p[1000005];
void bbd(int l1,int r1,int l2,int r2){
    int t=p[a[l1]];
    if(t>l2) bbd(l1+1,l1+t-l2,l2,t-1);
    if(t<r2) bbd(l1+t+1-l2,r1,t+1,r2);
    printf("%d ",a[l1]);
}
int main() {
    scanf("%d",&n);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    for(int i=0;i<n;i++){ 
	scanf("%d",&b[i]);
	p[b[i]]=i;
    }
		
    bbd(0,n-1,0,n-1);
    return 0;
}

二、堆

（一）什么是堆

堆是一种数组对象，它可以被视为一个完全二叉树。

堆有一种神奇的特性，如下图：

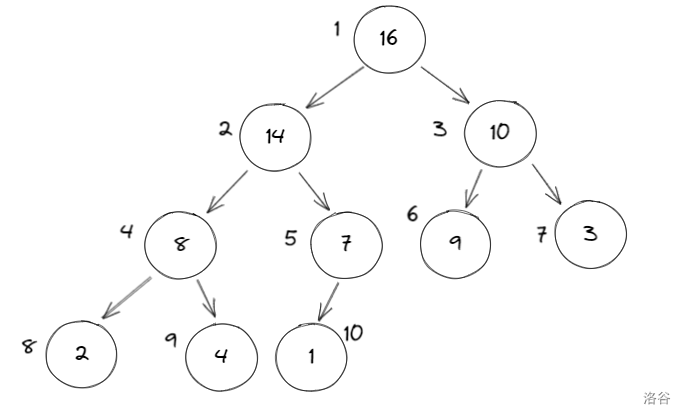
你会发现：设根的编号为 \(n\)，左儿子编号为 \(x\)，右儿子编号为 \(y\)，则：

• \(x=2 \times n\)
• \(y=2 \times n +1\)

堆分两种：对于除根节点以外的每个节点 \(i\)：

• \(A[parent(i)] \ge A[i]\)，称此堆为大根堆；
• \(A[parent(i)] \le A[i]\)，称此堆为小根堆。

（二）堆的操作

现在，我们以小根堆为例，讲一讲如何进行堆操作。（其实大根堆就改几个符号就行了）

一般来讲，堆有两种操作：

• \(put\) 函数，往堆中插入一个元素；
• \(get\) 函数，从堆中取出并删除一个元素。

\(put\) 函数

过程如下：

1. 往队尾加入一个元素，并把 \(now\) 设置为该节点所在位置 \(i\)；
2. 比较当前节点（\(now\)）与其父节点（\(now \div 2\)）的大小：
   若：
   • \(heap[now] < heap[now \div 2]\)：交换两个位置的值，重新做一遍第 \(2\) 步；
   • \(heap[now] \ge heap[now \div 2]\)：进行第 \(3\) 步。
3. 结束。

下面我们一步一步来分析：这是原树：

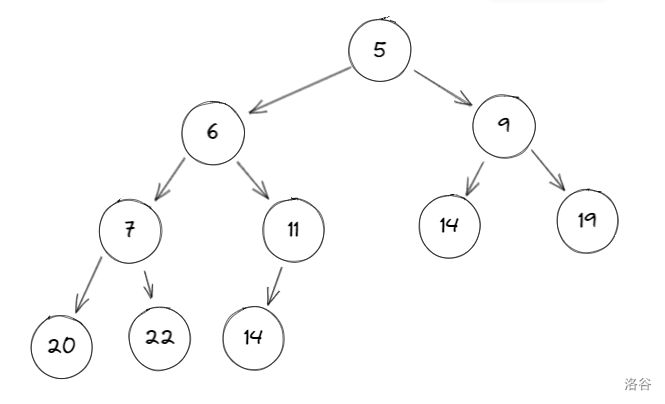
现在我们想在树当中插入 \(3\)，先添加到队尾：

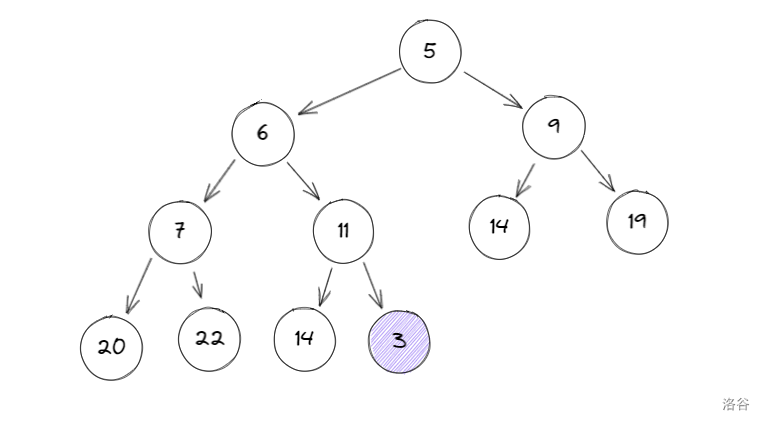
比较 \(3\) 与其父节点：\(3 < 11\)，与父节点交换：

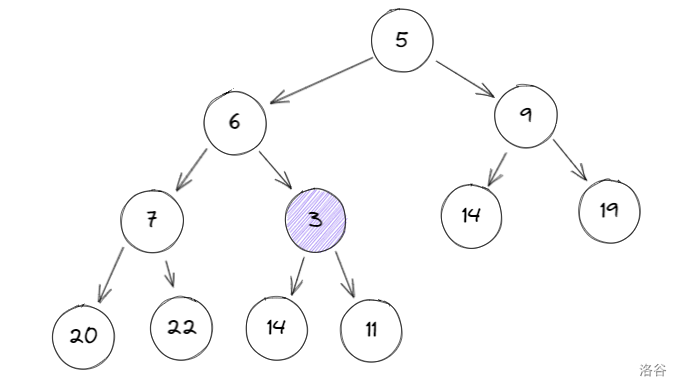
再进行一次 \(2\) 操作，比较 \(3\) 和 \(6\)，\(3 < 6\)：

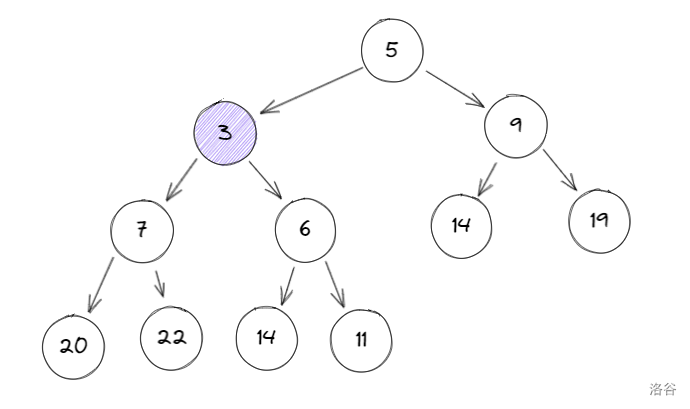
最后再比较一次 \(3\) 和 \(5\)，\(3 < 5\)：

至此，我们成功地插入了一个数进入一个堆。下面给出代码：

void put(int d)
{
    int now,next;
    heap[++heap_size]=d;
    now=heap_size;
    while(now>1){
        next=now/2;
        if(heap[now]>=heap[next]) break;
        swap(heap[now],heap[next]);
        now=next;
    }
}

\(get\) 函数

相应的，有进就也有出。

\(get\) 函数步骤如下：

1. 取出堆根节点的值；
2. 把堆的最后一个节点的值放到根的位置上，把根覆盖掉，并把堆的长度 \(-1\)；
3. 把根节点置为当前父节点（\(pa\) 变量）；
4. • 如果 \(pa\) 无儿子（\(pa>len \div2\)），进行第 \(6\) 步；
   • 如果 \(pa\) 有儿子（\(pa<= len \div 2\)），把 \(pa\) 两个（或一个）儿子中最小的那个置为当前子节点 \(son\)，进行第 \(5\) 步；
5. 比较 \(pa\) 和 \(son\) 的大小：
   • \(pa \le son\)，进行第六步；
   • \(pa > son\)，交换两者的值，把 \(pa\) 指向 \(son\)。
6. 结束。

仍以刚刚的图为例：

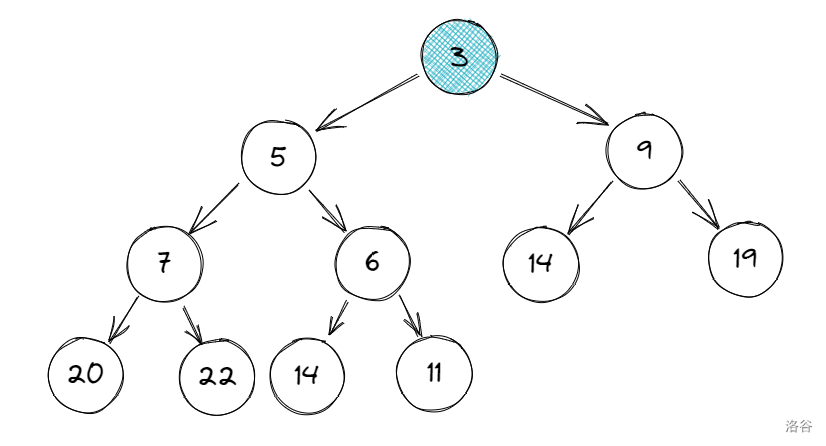
现在先去掉 \(3\)，把 \(11\) 作为根节点：

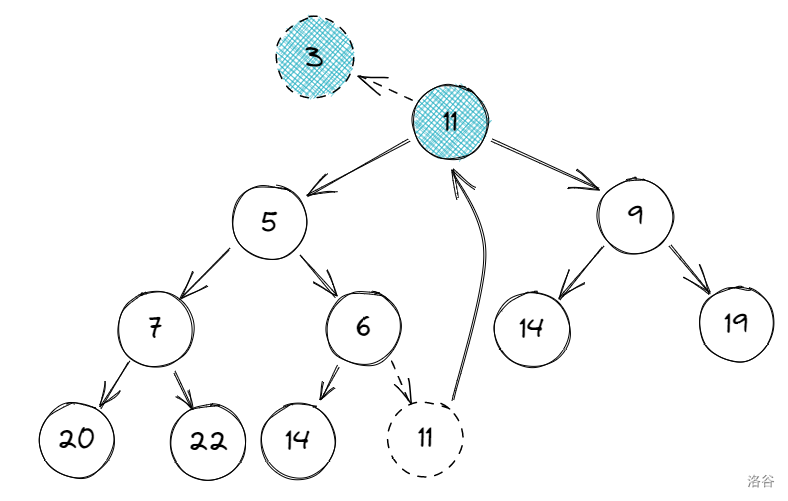
比较根节点的两个子节点大小：$ 5<9 \(，\)son$ 为 \(5\)。
又比较 \(5\) 和 \(11\) 的大小：$ 11>5$，交换两数位置：

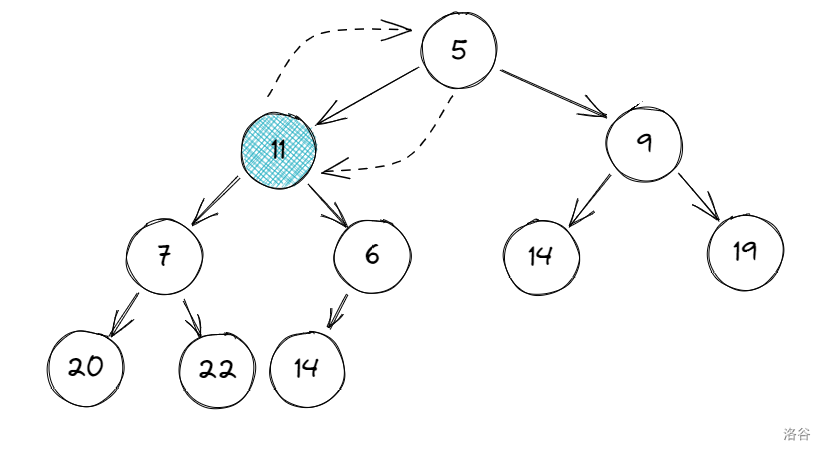
接着，又比较以 \(11\) 为根节点的两个子节点大小：\(7 >6\)。
比较 \(11\) 与 \(6\) 的关系：\(11>6\)，所以：

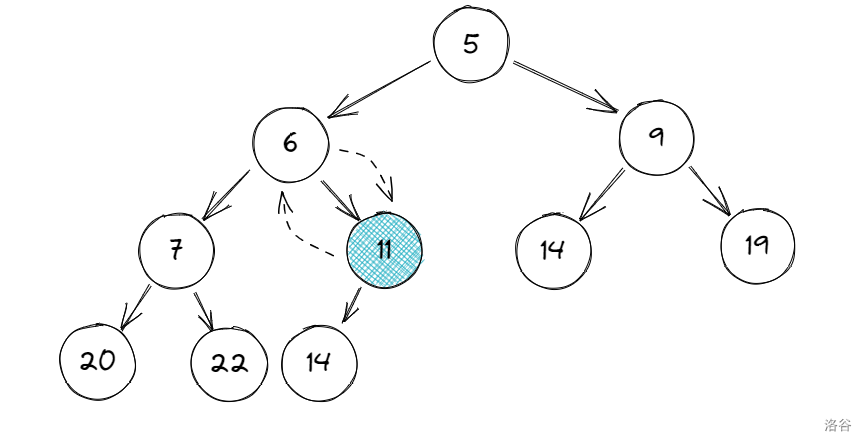
最后我们发现，\(11\) 唯一的子节点 \(14\) 已经比 \(11\) 大，于是结束操作。

给出详细代码：

int get(){
    int now,next,res;
    res=heap[1];
    heap[1]=heap[heap_size--];
    now=1;
    while(now*2<=heap_size){
	next=now*2;
	if(next<heap_size && heap[next+1]>heap[next]) next++;
	if(heap[now]>=heap[next]) break;
	swap(heap[now],heap[next]);
	now=next;
    }
    return res;
}

（三）堆排序

手动堆排序

假设有 \(n\) 个数字存放在 \(A[1,2,\cdots,n]\) 中，我们可以利用刚刚的 \(get\) 函数与 \(put\) 函数解决这个问题：

void heapsort(){
    for(int i=1;i<=n;i++)
        put(A[i]);
    for(int i=1;i<=n;i++)
        A[i]=get();
}

STL 堆排序

使用 priority_queue 可以非常轻松的实现堆排序。

（未待完续）