动态规划——一步一步走向爱
(2023.1)
前言
期末考试结束了,进入寒假集训,上9天,每天5小时,真够累的。
加油!变得越来越蒻,变得越来越强!
(未待完续)
NO.1 动态规划简述
20世纪50年代初,美国数学家R.E.Bellman(大佬)在研究多阶段决策的优化问题时,提出了有名的最优化原理:把多阶段过程转化为一系列单阶段问题,逐个求解。所以:一种新方法——动态规划(Dynamic Programming,简称dp)诞生了!
动态规划特点:
把一个大问题分解成若干个相似的小问题(也称子问题),按阶段逐个求解子问题的最优解,最终得到主问题最优解。
一般来讲,动态规划题目做题方法:
- 列表
- 按阶段讨论问题
- 作出最佳决策
- 推出状态转移方程(后面会说)
- 编程求解
(后面会详细描述)
NO.2 dp模型
分八个部分:
- 动规入门
- 最大连续子序列和
- 最长上升 or 下降子序列
- 分组
- 最长公共子串
- 最长公共子序列
- 矩阵
- 区间dp
一、动规入门:从一道例题开始

你也可以在这里找到题目。
好经典对不对?
学过搜索的我一看:深搜嘛,这么简单。但一看复杂度:\(O(2^{n-1})\)。我骂了娘。
好吧,我们换一种思路:
搜索是从上往下遍历每一个节点,那我们可不可以从下往上进行思考呢?
这是最先:
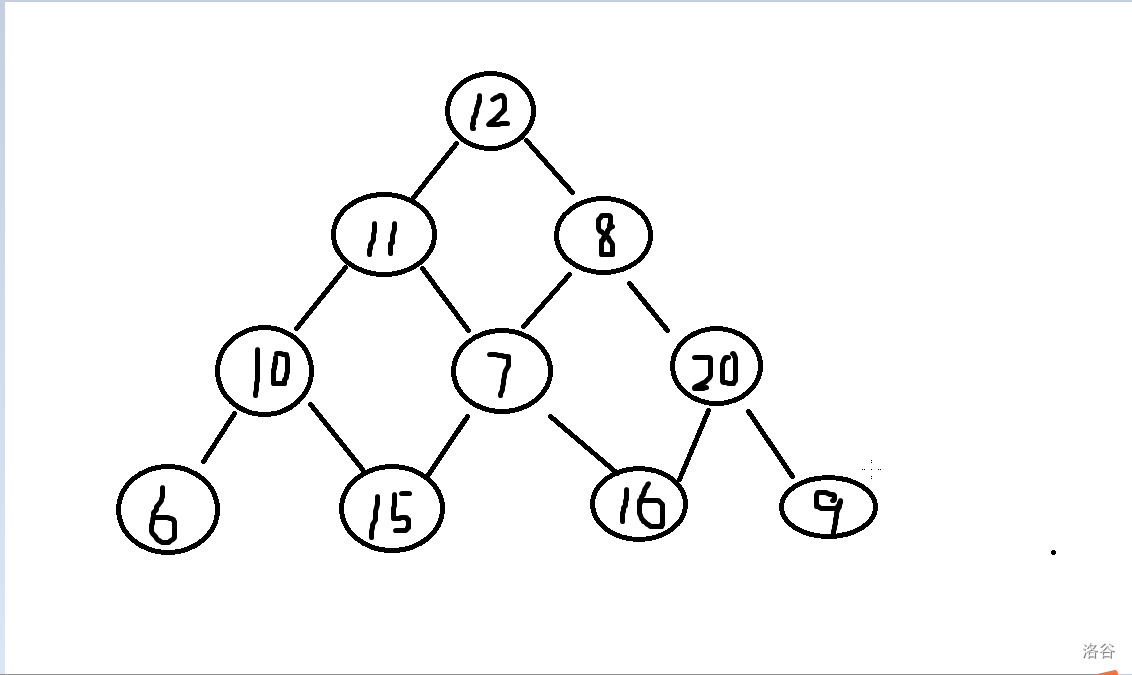
我们从第三层最右边开始看,如果要让结果最大,且经过 \(20\) 这个节点,\(16\) 和 \(9\) 明显选 \(16\),那 \(20\) 这个位置开始的最大值为:\(36\)。
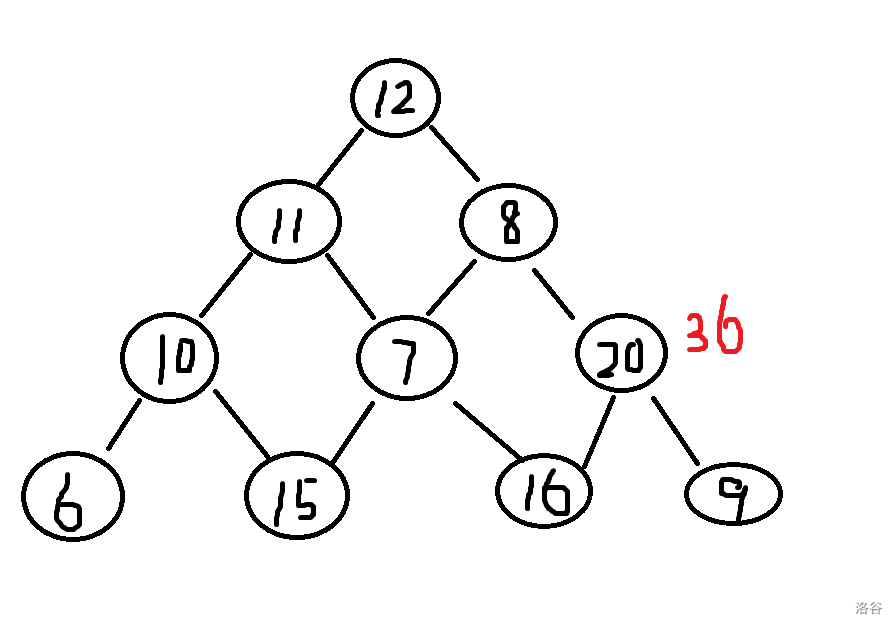
我们往左一点,到达 \(7\) 这个节点,最大就为:\(7+16=23\)。
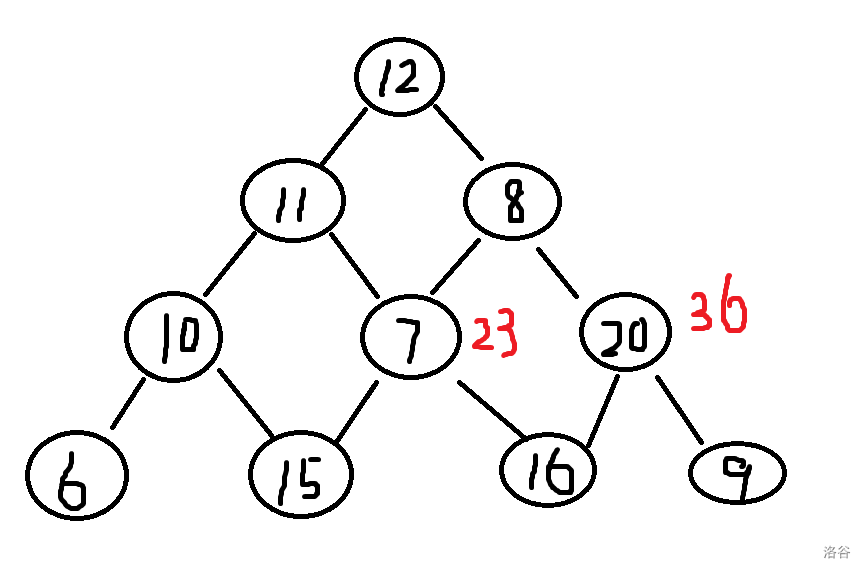
最左边,\(10\) 这个节点,最大值就为:\(10+15=25\)。
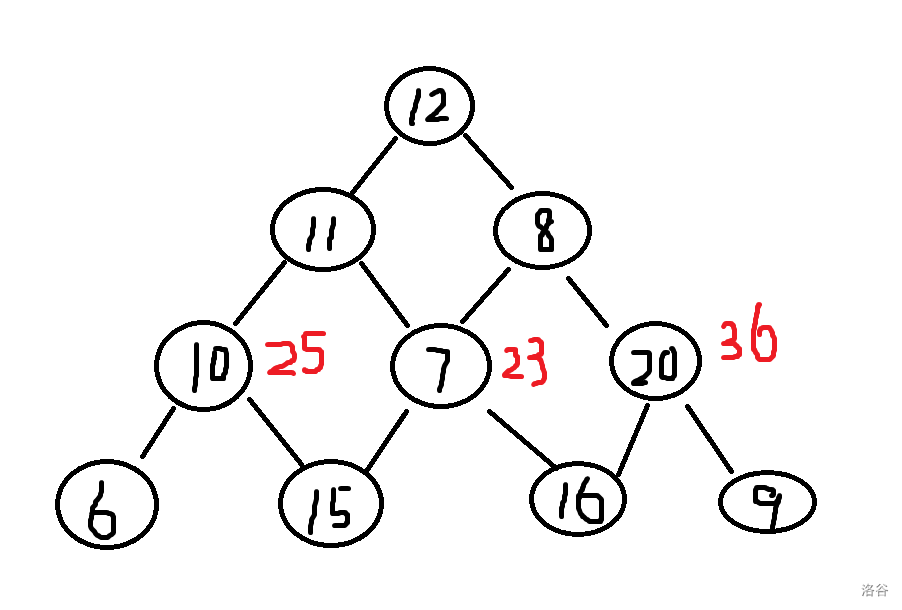
分析完第三层,我们回到第二层,用同样的办法可以得到:
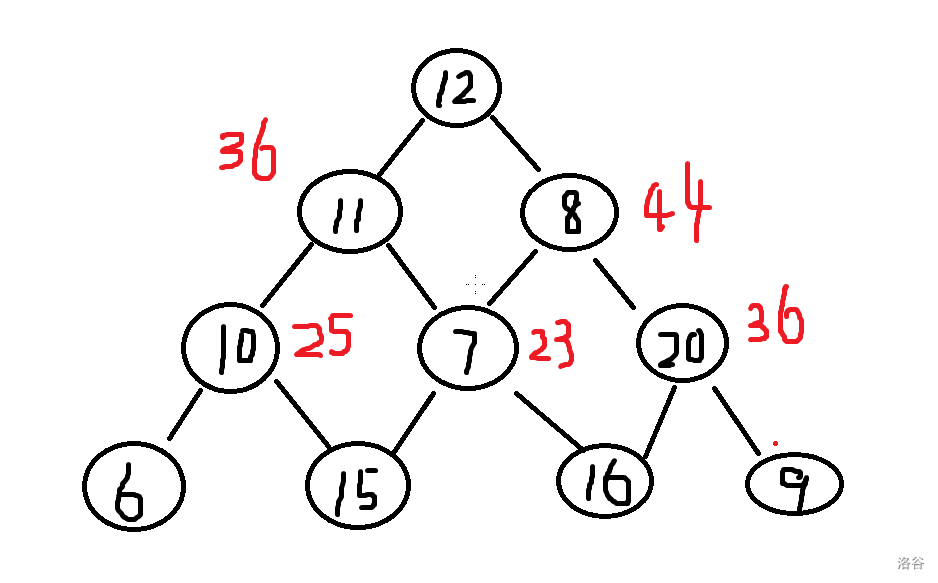
那起点最大值就有了:\(12+44=56\)。
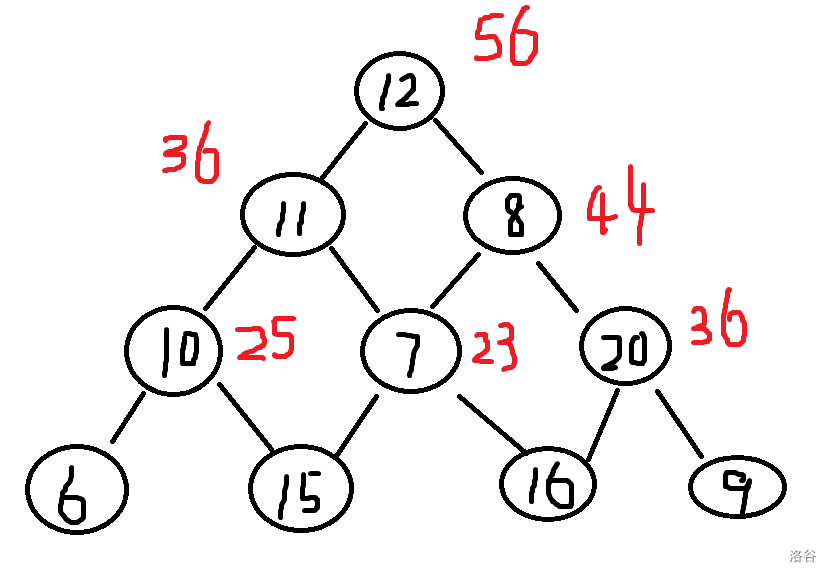
是不是很巧妙?那怎么用程序实现呢?
我们要开两个数组,具体作用如下:
int a[1005][1005];//a记录每个节点的值
int f[1005][1005];//f记录该节点数字和最大值
接下来我们要引入一个新概念:动态转移方程。
你可以不去想那些高深莫测的解释,动态转移方程就是说:把局部答案一步步转移为中心问题答案。
举个例子,这道题的动态转移方程为:
\(f[x][y]=a[x][y]+\max{(f[x+1][y],f[x+1][y+1])}\)
其中的\(f[x+1][y]\) 和 \(f[x+1][y+1]\) 就是 \(a[x][y]\) 下面的两个节点。
二、最大连续子序列和
什么是最大连续子序列和呢?
比方说,我给你 \(n\) 个数,有 \(i\) 和 \(j\) 两个位置(满足 \(1 \le i \le j \le n\)),从 \(i\) 开始的,到 \(j\) 结束,这期间所有的数的和最大,就成为最大连续子序列和。
你一定最开始想到的就是一次枚举 \(i\) 和 \(j\),反复求值,可是,你也知道会发生什么。
我们现在就要规避这个问题。
首先,运用贪心的思想,如何使和最大?当然了,尽量不要有负数存在(如果实在在规避不了我们也没办法)。
接着,我们考虑顺序。有一种思路是这样的:从右往左依次分析,若当前位置的数加上右边的数还比当前的数小(何苦为难自己?),就不加上右边的数。对于每一个位置的数,我们都这样分析,最后扫一遍,找到最大的位置。
最后,考虑动态转移方程。
如果 \(a\) 数组表示序列中的每一个数,\(f\) 表示该位置的最大值,可以推出:
\(f[x]=\begin{cases}f[i+1]+a[i]&f[i+1] >0\\a[i]&f[i+1] \le 0\end{cases}\)
边界条件:\(1 \le i \le n\)。
代码在这里啦:
#include<bits/stdc++.h>
using namespace std;
int n;
int a[3005];//记录每个位置数字
int f[3005];//f表示以位置为i开头的数字为开头的最大连续和。
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
//读入
f[n]=a[n];
for(int i=n-1;i>=1;i--){
if(f[i+1]<=0) f[i]=a[i];
else f[i]=a[i]+f[i+1];
}
//分两种情况
int ans=-10005;
for(int i=1;i<=n;i++) ans=max(ans,f[i]);
//寻找最大值
printf("%d",ans);
return 0;
}
三、最长上升 or 下降子序列
1.讲解
现在我们有 \(n\) 个数组成的序列,求里面最长的上升子序列。
例如这 \(n\) 个数分别是:\(3,8,7,14,10,55,12,23\)
记住,先分组:(最后一行代表 \(f[i]\):以位置为 \(i\) 数字开头的序列最大长度)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 3 | 8 | 7 | 14 | 10 | 55 | 12 | 23 |
从右往左,我们开始!
- \(23\):你就一个数,装什么装!\(f[8]=1\);
- \(12\):往后枚举,只有一个,并且比 \(12\) 大,所以:\(f[7]=1+f[8]=2\);
- \(55\):比较可怜,比后面的数都大,于是:\(f[6]=1\)
- \(10\):我们一看,诶?\(12\) 和 \(23\) 都比你大,选哪个呢?很明显,\(f[7] > f[8]\),所以我们选 \(12\):\(f[5]=1+f[7]\);
- \(14\):\(55\) 和 \(23\) 都有能力竞争,但因为 \(f[6] = f[8]\),所以不了了之:\(f[4]=1+f[6]=1+f[8]=2\);
- \(7\):一看是个小不点儿,直接有:\(f[3]=1+f[5]=4\);
- \(18\):\(18\) 就有一些倒霉了,又是 \(55\) 和 \(23\) 来竞争,随便一个:\(f[2]=1+f[6]=1+f[8]=2\);
- \(3\):重头戏来也!我们一看,\(7\) 获得了青睐,所以:\(f[1]=1+f[3]=5\)
至此,枚举完毕。肉眼可见,第 \(1\) 位的 \(3\) 获得胜利,所以最长上升子序列长度为:\(5\)!
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 3 | 8 | 7 | 14 | 10 | 55 | 12 | 23 |
| 5 | 2 | 4 | 2 | 3 | 1 | 2 | 1 |
状态转移方程很简单:\(f[i]=1+\max {(f[j])}\),并且满足 $ i < j \le n$。
程序于是油然而生:
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
f1[i]=1;//注意这里!很重要
}
for(int i=n-1;i>=1;i--)
for(int j=i+1;j<=n;j++)
if(a[i]>a[j] && f1[i]<=1+f1[j])
f1[i]=1+f1[j];
那所以最长下降子序列还那么?改几个符号便有了嘛:
for(int i=2;i<=n;i++)
for(int j=1;j<i;j++)
if(a[i]>a[j] && f2[i]<=1+f2[j])
f2[i]=1+f2[j];
(当然:还是要特别注意区分。十年OI一场空,没分大小见祖宗)
2.例题
一道老题:合唱队形
这道题其实分为两部分:求上升子序列和下降子序列。注意,我没有加“最长”。
怎么动态规划前面已经说过,这里讲一下最后求值的过程。
我们的 \(f1\) 数组代表上升子序列,\(f2\) 数组代表下降子序列。对于 \(f1\),我们每一个 \(i\) 指的是以第 \(i\) 个数为开头的上升子序列;对于 \(f2\),我们每一个 \(i\) 指的是以第 \(i\) 个数为结尾的下降子序列。所以,\(f1[i]+f2[i]-1\) 就是满足题目条件的队形长度,最后计算出队人数就是 \(n-\max{(f1[i]+f2[i]-1)}\)。
注意:此处有一个小小的 \(-1\),因为两个数组都包含 \(a[i]\),所以 \(s[i]\) 重复算了两次,要去掉。
一些可以练习的题目:
四、分组

现在我们来看这道题。
随便举一个例子:现在我们要走 \(10\) km。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| 12 | 21 | 35 | 40 | 49 | 58 | 69 | 79 | 90 | 101 |
最后一行代表 \(f[i]\),即行驶 \(i\) 公里的最小费用。
- \(i=1\):\(f[1]=12\)
- \(i=2\):两种选择:
\(f[2]=\min\begin{cases}f[1]+f[1]=24\\a[2]=21\end{cases}\)
所以我们选择第二种:\(f[2]=21\) - \(i=3\):两种选择:
\(f[3]=\min\begin{cases}f[1]+f[2]=33\\a[3]=35\end{cases}\)
显然:\(f[3]=f[1]+f[2]=33\) - \(i=4\):三种选择:
\(f[4]=\min\begin{cases}f[1]+f[3]=45\\f[2]+f[2]=42\\a[4]=40\end{cases}\)
所以:\(f[4]=a[4]=40\)
$ \cdots \cdots$
最后的表就是这样:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| 12 | 21 | 35 | 40 | 49 | 58 | 69 | 79 | 90 | 101 |
| 12 | 21 | 33 | 40 | 49 | 58 | 69 | 79 | 89 | 98 |
那所以行驶 \(10\) 公里最少就需要 \(98\) 元。
现在我们来归纳一下方程:
- 当 \(want \le 10\) 时,最小值在其所有拆分数字最小值和以及 \(a[i]\) 中选。
- 当 \(wang >10\) 时,最小值只在其所有拆分数字最小值和中选。
列出方程:
\(f[want]=\begin{cases}\min{(a[i],f[i]+f[i-j])}&want \le 10\\\min{(f[i]+f[i-j])}&want>10\end{cases}\)
至此,这一问题迎刃而解。
五、最长公共子串
先说一下子串和子序列的区别。
若没有特殊限制(比如最大连续子序列和),区别如下:
- 子串:一个序列中连续的一串数;
- 子序列:一个序列中按顺序选取的任意一串数。
好,我们步入正题:最长公共子串。
我们现在有 \(A\) 和 \(B\) 两个序列,分别如下:
\(A\):\(1,5,3,2,3\)
\(B\):\(2,3,5,3,2,5,3\)
人脑直接看出,最长公共子串为 \(5,3,2\)。如何编程实现?
我们先列一个表来分析:
左边是 \(A\),上面是 \(B\)。
| 2 | 3 | 5 | 3 | 2 | 5 | 3 | |
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 5 | |||||||
| 3 | |||||||
| 2 | |||||||
| 3 |
现在,如果对应位置行、列数字一样,我们标 \(1\)。
| 2 | 3 | 5 | 3 | 2 | 5 | 3 | |
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 5 | 1 | 1 | |||||
| 3 | 1 | 1 | 1 | ||||
| 2 | 1 | 1 | |||||
| 3 | 1 | 1 | 1 |
你发现了什么?我们肉眼看出的 \(5,3,2\) 就是下面这一条:
| 2 | 3 | 5 | 3 | 2 | 5 | 3 | |
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 5 | 1 | 1 | |||||
| 3 | 1 | 1 | 1 | ||||
| 2 | 1 | 1 | |||||
| 3 | 1 | 1 | 1 |
可以得到一个结论:每条左上往右下的斜线就包含了一种配对方式!
现在我们把这个表稍微变一下:
| 2 | 3 | 5 | 3 | 2 | 5 | 3 | |
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 5 | 1 | 1 | |||||
| 3 | 1 | 2 | 2 | ||||
| 2 | 1 | 3 | |||||
| 3 | 2 | 1 | 1 |
你发现了么?每个数字就代表以这个位置对应的行、列数为结尾的子串长度!
由此得出状态转移方程:
\(dp[i][j]=\begin{cases}dp[i-1][j-1]+1&A[i]=B[j]\\0&A[i] \ne B[i]\end{cases}\)
上代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[505];
int b[505];
int dp[505][505];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++) scanf("%d",&b[i]);
int ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i]==b[j]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=0;
ans=max(ans,dp[i][j]);
}
}
printf("%d",ans);
}
六、最长公共子序列
说完了子串,我们来谈子序列。由于子序列不一定连续的特性,我们的过程会稍微复杂一些。
我们仍然有两个序列:\(A\) 和 \(B\)。
-
阶段:以每一个元素作为阶段,从前往后讨论序列中的每一个元素。
-
决策:分两种情况
-
当 \(A_i=B_j\) 时,只需求出 \(<A_1,A_2,A_3,\cdots,A_{i-1}>\) 和 \(<B_1,B_2,B_3,\cdots,B_{j-1}>\) 的最长公共子序列
-
当 \(A_i \ne B_j\) 时,考虑递推的特性,又要分两种情况:
- 设 \(X\) 为 \(<A_1,A_2,A_3,\cdots,A_{i-1}>\) 和 \(<B_1,B_2,B_3,\cdots,B_j>\) 的最长公共子序列;
- 设 \(Y\) 为 \(<A_1,A_2,A_3,\cdots,A_i>\) 和 \(<B_1,B_2,B_3,\cdots,B_{j-1}>\) 的最长公共子序列;
则 \(\max{(X,Y)}\) 即为所求。
-
-
状态:我们用 \(f[i][j]\) 来表示 \(A\) 序列的前 \(i\) 项和 \(B\) 序列的前 \(j\) 项的最大公共子序列的长度。
-
方程:
\(f[i][j]=\begin{cases}f[i-1][j-1]+1&A[i]=B[j]\\\max{(f[i-1][j],f[i][j-1])}&A[i] \ne B[i] \\ 0&i=0 \text{或} j=0\end{cases}\)
其实程序跟最长公共子串没多大区别:
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[505];
int b[505];
int dp[505][505];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++) scanf("%d",&b[i]);
int ans=0;
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
if(i==0 || j==0) dp[i][j]=0;
else if(a[i]==b[j]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
ans=max(ans,dp[i][j]);
}
}
printf("%d",ans);
}
我们来拓展一下,如果求三个数的最长公共子序列怎么办?换汤不换药,你可以列出以下方程:
\(f[i][j][k]=\begin{cases}f[i-1][j-1][k-1]+1&A[i]=B[j]=C[i]\\\max{(f[i][j][k-1],f[i-1][j-1][k])}&A[i] = B[i] \ne C[i]\\\max{(f[i][j-1][k],f[i-1][j][k-1])}&A[i] = C[i] \ne B[i]\\\max{(f[i-1][j][k],f[i][j-1][k-1])}&B[i]=C[i] \ne A[i]\\\max{(f[i-1][j][k],f[i][j-1][k],f[i][j][k-1],f[i-1][j-1][k],f[i-1][j][k-1],f[i][j-1][k-1])}&A[i] \ne B[i] \ne C[i]\\ 0&i=0 \text{或} j=0 \text{或} k=0\end{cases}\)
晕了么?没事,看代码更晕:
#include<bits/stdc++.h>
using namespace std;
int n,m,u;
int a[205];
int b[205];
int c[205];
int dp[205][205][205];
int main(){
scanf("%d%d%d",&n,&m,&u);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++) scanf("%d",&b[i]);
for(int i=1;i<=u;i++) scanf("%d",&c[i]);
int ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int k=1;k<=u;k++){
if(a[i]==b[j] && b[j]==c[k]) dp[i][j][k]=dp[i-1][j-1][k-1]+1;
else if(a[i]==b[j] && b[j]!=c[k]) dp[i][j][k]=max(dp[i][j][k-1],dp[i-1][j-1][k]);
else if(a[i]!=b[j] && b[j]==c[k]) dp[i][j][k]=max(dp[i-1][j][k],dp[i][j-1][k-1]);
else if(a[i]==c[k] && b[j]!=c[k]) dp[i][j][k]=max(dp[i][j-1][k],dp[i-1][j][k-1]);
else dp[i][j][k]=max(max(dp[i-1][j][k],dp[i][j-1][k]),max(max(dp[i][j][k-1],dp[i-1][j-1][k]),max(dp[i-1][j][k-1],dp[i][j-1][k-1])));
ans=max(ans,dp[i][j][k]);
}
}
}
printf("%d",ans);
}
七、矩阵
(一)边长最大子矩阵
你现在有一块 \(n \times m\) 的土地,你想在上面一个个最大的正方形房屋。若一个位置上标的是 \(0\) 说明这个地方不能建,\(1\) 说明可以。现在要求你编程求出这个正方形房屋的最大边长。
例如:
输入:
4 4
0 1 1 1
1 1 1 0
1 1 1 0
1 1 1 1
输出:
3
我们一步一步来分析:
- 阶段:从上往下,从左往右一次讨论矩阵中的每一个数字。
- 状态:我们用 \(dp[i][j]\) 表示把点 \((i,j)\) 当做一个正方形对角线右下角的端点可以形成的最大正方形边长。
- 决策:
这是按照“状态”一步所得出来的关系:
我们把目光看向位于 \((3,3)\) 位置的 \(2\),它是怎么得到的?位于 \((2,3)\) 和 \((3,2)\) 位置的两个数都为 \(2\),只有 \((2,2)\) 位置的数为 \(1\)。因为 \((1,1)\) 是 \(0\) 的限制,\((2,2)\) 位置只能为 \(1\),从而继续限制了 \((3,3)\) 位置只能为 \(2\)。你明白了么?某个点的值只受其左上、上、左三个点中最小值的影响。0 1 1 1 1 1 2 0 1 2 2 0 1 2 3 1 - 有了前面的铺垫,状态转移方程有了:
\(f[i][j]=\begin{cases}1+\min{(f[i-1][j-1],f[i-1][j],f[i][j-1])}&a[i][j]=1\\ 0&a[i][j]=0\end{cases}\)
边界条件:\(1 \le i \le n\),\(1 \le j \le m\)
上代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
int p[1005][1005];
int dp[1005][1005];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
scanf("%d",&p[i][j]);
}
int ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(p[i][j]==0) dp[i][j]=0;
else dp[i][j]=1+min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]));
ans=max(ans,dp[i][j]);
}
printf("%d",ans);
}
(二)最大子矩阵
你现在有一个 \(n \times n\) 的矩阵,每个位置上都有一个数,你需要选取一个矩形,使其中数字之和最大。
例如输入:
4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
其中最大的矩阵就是这里:
9 2
-4 1
-1 8
所以输出:
15
对于像我这种钟爱暴力的人来说,此题简直就是天赐良缘啊!(⁄(⁄ ⁄•⁄ω⁄•⁄ ⁄)⁄)
遥想当年,我通过暴力秒了好多题,现在却沦落天涯。
扯远了,我们看这道题怎么做。其实这道题的正解和暴力真的沾边哟!
对于一个新知识,我们要想方设法把他转换成旧知识,例如这道题。以下是思维过程:
- 既然想要我们选取一个矩形,那自然义不容辞,每个矩形都要考虑。如何遍历每一个矩形?可以这样:用 \(i\) 和 \(j\) 来模拟矩形的高,即从第 \(i\) 行到第 \(j\) 行为矩形的高,一个朴素的二层循环就有了。
- 有了高还不行,得有宽,那宽不会也要那双重循环来做吧?肯定不会。想想之前学过的什么?最大连续子序列和!我们把从 \(i\) 行到 \(j\) 行的每一列数相加,就得到一个序列,再用最大连续子序列和来求我们需要的值!
- 相加好慢哟!别急,之前不是学过前缀和么?运用前缀和求解岂不是就快多了?
- 那如何储存每次算出的最大值呢?我们有三个变量:\(i\)、\(j\) 和 \(k\)。所以,自然要一个三维数组的啦!定义 \(dp[i][j][k]\):从 \(i\) 行到第 \(j\) 行以第 \(k\) 列为结尾的最大子矩阵。
一张图帮你更好理解:

上代码:
#include<bits/stdc++.h>
using namespace std;
int n;
int p[105][105];
int t[105];
int dp[105][105][105];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
scanf("%d",&p[i][j]);
p[i][j]=p[i][j]+p[i-1][j];
}
int ans=-999999999;
for(int i=1;i<n;i++)
for(int j=i;j<=n;j++){
for(int k=1;k<=n;k++) t[k]=p[j][k]-p[i-1][k];
dp[i][j][n]=t[n];
ans=max(ans,dp[i][j][n]);
for(int k=n-1;k>=1;k--){
if(dp[i][j][k+1]<=0) dp[i][j][k]=t[k];
else dp[i][j][k]=t[k]+dp[i][j][k+1];
ans=max(ans,dp[i][j][k]);
}
}
printf("%d",ans);
}
八、区间dp
有一点难,我也是理解了好久才明白的。来看一道经典例题:
在操场上沿一直线排列着 \(n\) 堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的两堆石子合并成新的一堆, 并将新的一堆石子数记为该次合并的得分。允许在第一次合并前对调一次相邻两堆石子的次序。
计算在上述条件下将 \(n\) 堆石子合并成一堆的最小得分。
这个问题复杂了些,我们把“允许在第一次合并前对调一次相邻两堆石子的次序”去掉来分析这道题:
我们用几张图来表达一下:
这是最先:
如果两两合并最小值:
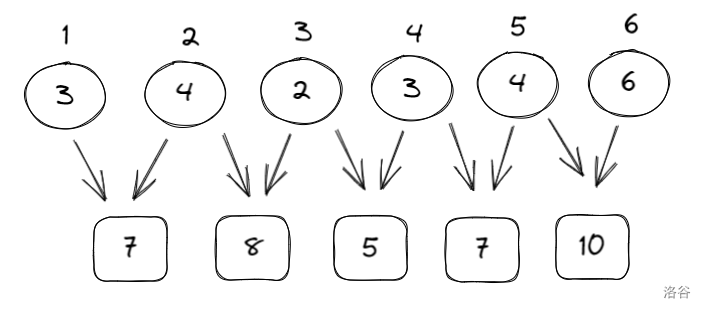
三堆三堆合并最小值:
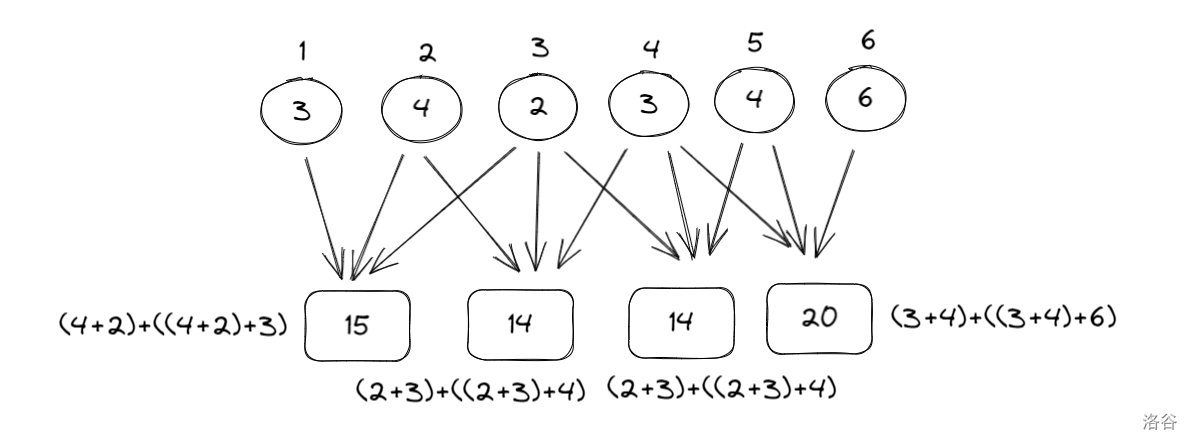
四堆四堆合并最小值:
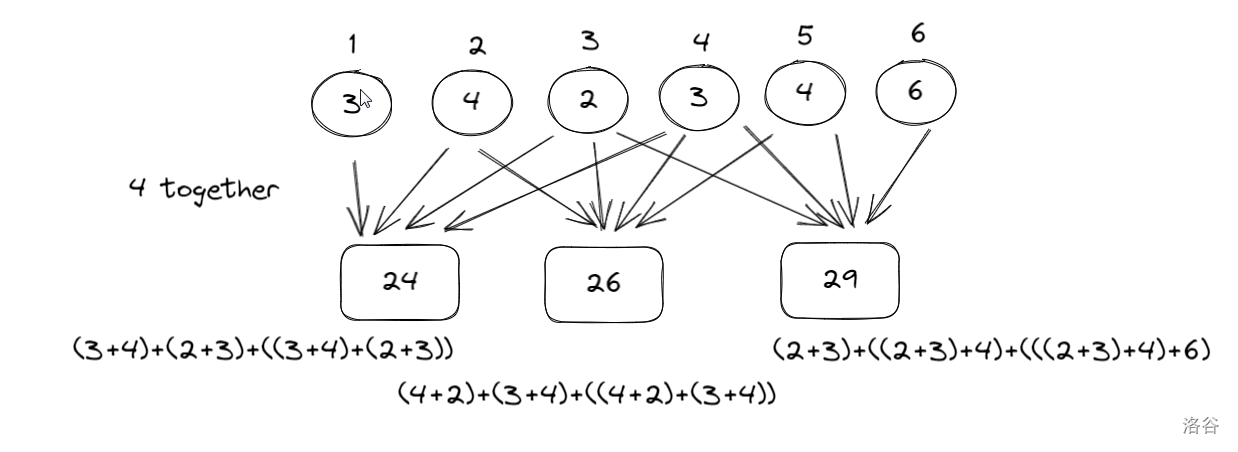
五堆五堆合并最小值:
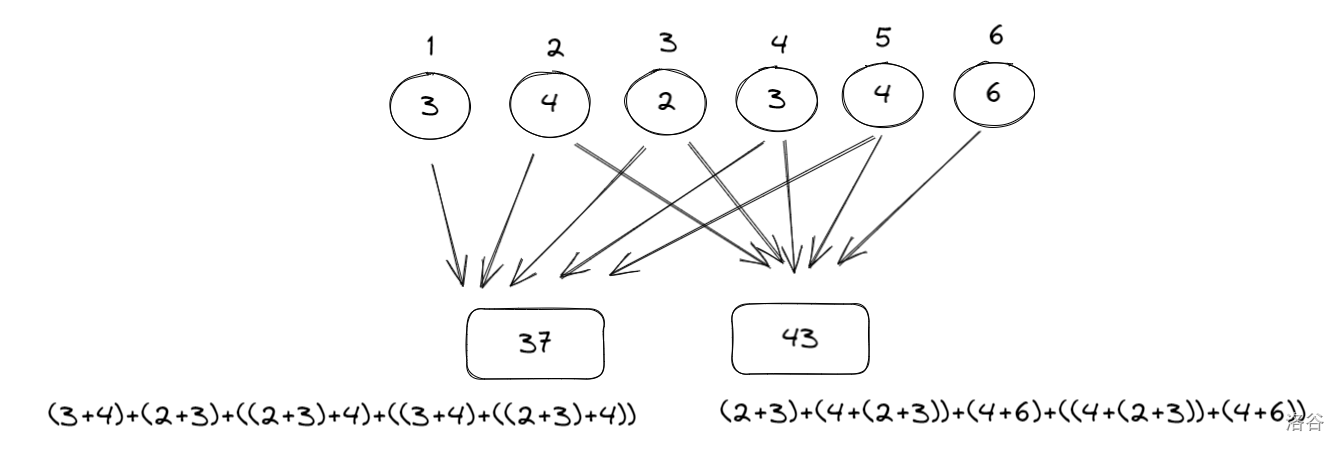
最后的最小值:
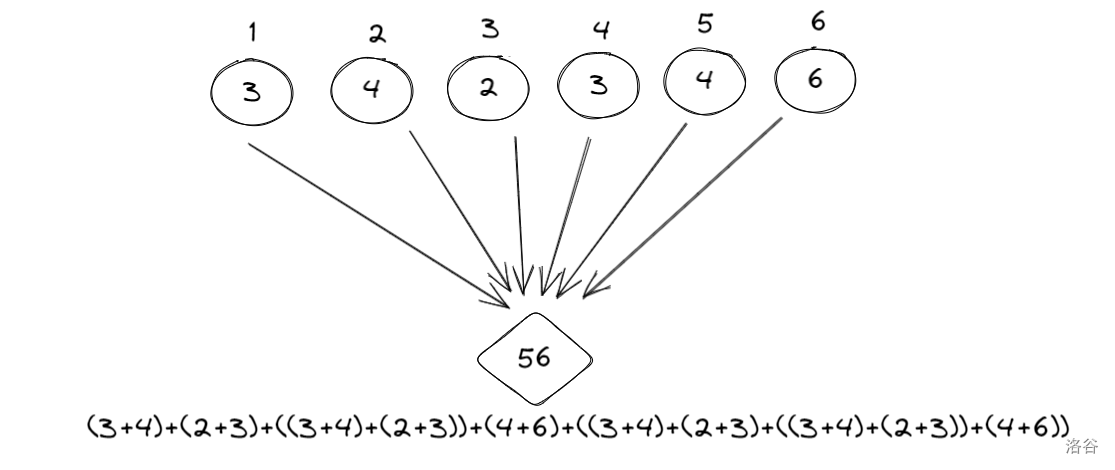
最后的合并过程:
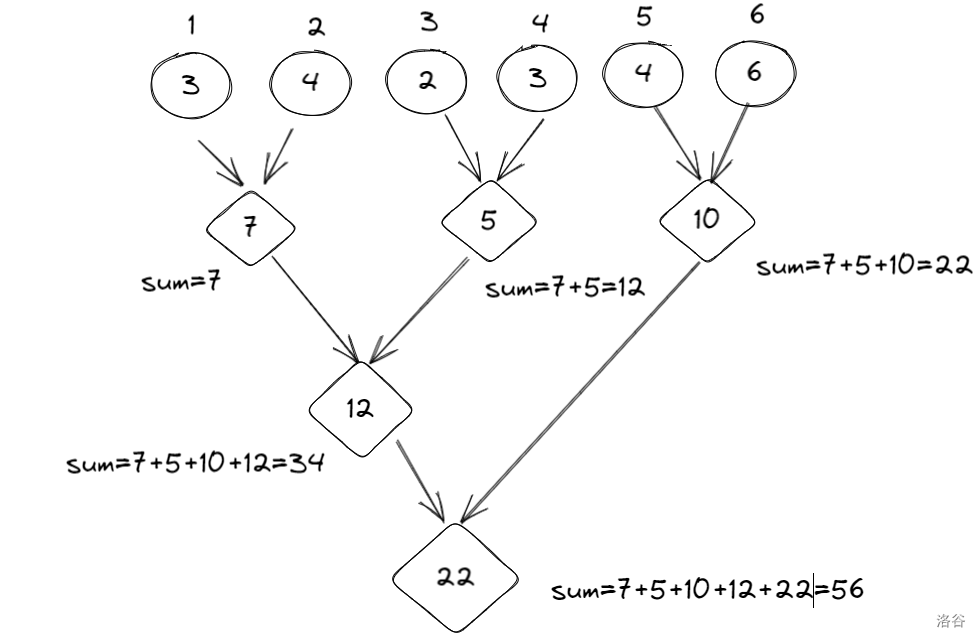
相信你已经明白了,思路如下:
- 阶段:按每次合并的堆数来分阶段(一堆一堆合并,两堆两堆,三堆三堆……)
- 状态:\(f[i][j]\) 代表从第 \(i\) 堆石子开始的连续 \(j\) 堆合并的最小值。
- 决策:当前这块石头,以何处为界,划分成两部分。
- 方程:
\(f[i][j]=\sum_{i}^{j}{A_i} + \min{(f[i][k]+f[i+k][j-k])}\)
边界条件:\(1 \le k \le j-1\)
现在我们把那个暂时放置的条件加上,无非就是多一层暴力来枚举交换哪两个数,用 \(swap\) 即可。
代码:
#include<bits/stdc++.h>
using namespace std;
int n;
int sum[105];
int f[105][105];
void clear(){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
f[i][j]=INT_MAX;
f[i][1]=0;
}
}
int tot(int i,int j){
int t=0;
for(int w=i;w<=j;w++) t+=sum[w];
return t;
}
int dp(){
for(int j=2;j<=n;j++){
for(int i=1;i<=n-j+1;i++){
for(int k=1;k<j;k++){
f[i][j]=min(f[i][j],tot(i,i+j-1)+f[i][k]+f[i+k][j-k]);
}
}
}
return f[1][n];
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&sum[i]);
}
int ans=999999999;
for(int i=1;i<n;i++){
clear();
swap(sum[i],sum[i+1]);
ans=min(ans,dp());
swap(sum[i],sum[i+1]);
}
printf("%d",ans);
}
NO.3 01背包
一:
来看一道经典例题:
一个背包容积为 \(T(0 \le T \le 2000)\),现在有 \(N(0 < N \le 1000)\) 个物品,每个物品有一定体积 \(V(1 \le V \le 5000)\)。从这 \(N\) 个物品中选取若干个装入背包内,使背包所剩的空间最小。请求出最小的剩余空间。
很容易想到二维数组动态规划:用 \(f[i][j]\)(\(bool\) 型)来求能否用前 \(i\) 个物品求出总体积为 \(j\)。但二维数组显然空间复杂度很高,我们可不可以优化呢?
所以,我们的滚动数组+01背包闪亮登场!
现在我们用 \(f[j]\) 表示所有数能否得到 \(j\) 体积,然后重点来了:边输入边进行枚举,求出前 \(i\) 个数所能得到的所有体积。
例如,背包体积为 \(10\),有 \(4\) 个物品,体积分别是:\(2\),\(3\),\(5\),\(7\)。
一开始:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 原来: | 1 | ||||||||||
| 2 | |||||||||||
| 3 | |||||||||||
| 4 | |||||||||||
| 5 |
加入 \(2\) 之后
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 原来: | 1 | ||||||||||
| 2 | 1 | ||||||||||
| 3 | |||||||||||
| 4 | |||||||||||
| 5 |
还有 \(3\):
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 原来: | 1 | ||||||||||
| 2 | 1 | 1 | |||||||||
| 3 | 1 | 1 | 1 | 1 | |||||||
| 4 | |||||||||||
| 5 |
其中:\(5=2+3\)
增加 \(4\):
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 原来: | 1 | ||||||||||
| 2 | 1 | 1 | |||||||||
| 3 | 1 | 1 | 1 | 1 | |||||||
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
| 5 |
其中:\(6=2+4,7=3+4,9=2+3+4\)
最后:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 原来: | 1 | ||||||||||
| 2 | 1 | 1 | |||||||||
| 3 | 1 | 1 | 1 | 1 | |||||||
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
所以,这几种体积的物品最大可以构成 \(10\)(把背包填满)。
#include<iostream>
using namespace std;
int t,n,v;
bool f[5005];
int main(){
scanf("%d%d",&t,&n);
f[0]=1;
while(n--){
scanf("%d",&v);
for(int i=t;i>=v;i--) f[i]=f[i] || f[i-v];
}
for(int i=t;i>=0;i--)
if(f[i]){
printf("%d",t-i);
break;
}
return 0;
}
特别注意:
for(int i=t;i>=v;i--) f[i]=f[i] || f[i-v];
这是从大到小枚举!
为什么呢?
如果我们从小到大看看:
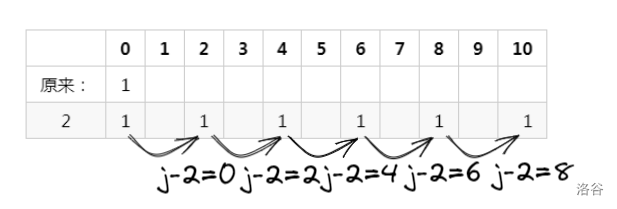
我们会发现,如果从小到大去枚举,则会有无限的多个符合条件的(即 \(a_i\) 的所有倍数)。这种结论是否意味着无用呢?肯定不是,且看下面这道题:
一个背包容积为 \(T(0 \le T \le 2000)\),现在有 \(N(0<N \le 1000)\) 种物品,每种物品有一定体积 \(V(1 \le V \le 5000)\)。每种物品有无限多个。从这N种物品中选取若干个装入背包内,使背包所剩的空间最小。请求出最小的剩余空间?
只需把上面的那个程序关键语句改为:
for(int i=v;i<=t;i++) f[i]=f[i] || f[i-v];
总结一下:
- \(j\) 从小到大:无限物品
- \(j\) 从大到小:单个物品
二:
刚刚的例子中只有一个变量:体积,现在我们加入另一个变量:价值。
一个背包容积为 \(T(0 \le T \le 2000)\),现在有 \(N(0<N \le 1000)\) 个物品,每个物品有一定体积 \(V(1 \le V \le 5000)\)。每个物品有一定价值 \(W(1 \le W \le 5000)\)。从这 \(N\) 个物品中选取若干个装入背包内,使背包总价值最大。请求出最大价值。
我们联系一下上一道题,上一道题我们用了 \(bool\) 来存,这次要我们求最大价值,自然要用 \(int\) 来存。上一题中,\(f[i-v]\) 是用来判断该位置是否可以有新的组合方式,那如果说我们在上一个可能有的组合方式上加上这一次物品的价值,就可以在新的组合方式上保存新的最大价值:
for(int i=1;i<=n;i++){
for(int j=t;j>=v[i];j--){
f[j]=max(f[j],f[j-v[i]]+m[i]);
}
}
最后,我们遍历一遍数组,找到最大的 \(f[i]\) 即可。
三:例题:
母牛的货币系统
母牛们不但创建了他们自己的政府而且选择了建立了自己的货币系统。他们对货币的数值感到好奇。
传统地,一个货币系统是由 \(1,5,10,20\) 或 \(25,50,100\) 的单位面值组成的。
母牛想知道有多少种不同的方法来用货币系统中的货币来构造一个确定的数值。
举例来说, 使用一个货币系统 \(1,2,5,10,\cdots\) 产生 \(18\) 单位面值的一些可能的方法是:\(18 \times 1, 9 \times 2, 8 \times 2+2 \times 1, 3\times 5+2+1\),等等其它。写一个程序来计算有多少种方法用给定的货币系统来构造一定数量的面值。保证总数将会适合 \(long long (C/C++)\) 和 \(Int64 (Free Pascal)\)。
此题非常简单,如何把他联系上背包?
- 要构建的面值:背包容积
- 货币:物品
货币面额:物品体积 - 题目没有要求货币数量:物品数量无限——\(j\) 从小到大
此题为以不同的一点是要求出总共的组合方法个数,那对于第 \(i\) 种面额的纸币,直接枚举 \(j\),在 \(f[j]\) 上加上 \(f[j-a[i]]\) 就行了。
#include<iostream>
using namespace std;
int t,n,v;
long long f[10005];
int a[100];
int main(){
scanf("%d%d",&n,&t);
f[0]=1;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i=1;i<=n;i++){
for(int j=a[i];j<=t;j++) f[j]+=f[j-a[i]];
}
printf("%lld",f[t]);
return 0;
}
金明的预算方案
这道题我们重在初始化,你当然可以存 \(m\) 个数,但是我这里有另一种做法:
先整一个结构体:
struct bbd{
int pz;//主件价格
int wz;//主件重要程度
int p=0;//附件个数
struct xbc{
int pf;//附件价格
int wf;//附件重要程度
}b[65];
}a[65];
接着输入:
scanf("%d%d%d",&x,&y,&z);
其中 \(x\) 代表第 \(i\) 件物品价格,\(y\) 代表重要程度,\(z\) 代表其对应的主件。
分情况讨论:
if(z==0){
t[i]=true;
a[i].pz=x;
a[i].wz=y;
a[i].p=0;
}
else{
a[z].p++;
a[z].b[a[z].p].pf=x;
a[z].b[a[z].p].wf=y;
}
如何进行 \(01\) 背包呢?
我们有五个决策:
- 不选该主件
- 只选该主件
- 选主件+\(1\) 号附件
- 选主件+\(2\) 号附件
- 选主件+\(1\) 号附件+\(2\) 号附件
因为每种物件都只有 \(1\) 件,\(j\) 就从大到小循环。
for(int i=1;i<=m;i++){
if(t[i]==false) continue;
if(a[i].p==0){//没有附件的主件
for(int j=N;j>=a[i].pz;j--)
f[j]=max(f[j],f[j-a[i].pz]+a[i].pz*a[i].wz);
}
else if(a[i].p==1){//有一件附件的主件
for(int j=N;j>=0;j--){
if(j>=a[i].pz) f[j]=max(f[j],f[j-a[i].pz]+a[i].pz*a[i].wz);
if(j>=a[i].pz+a[i].b[1].pf) f[j]=max(f[j],f[j-a[i].pz-a[i].b[1].pf]+a[i].pz*a[i].wz+a[i].b[1].pf*a[i].b[1].wf);
}
}
else{//有两件附件的主件
for(int j=N;j>=0;j--){
if(j>=a[i].pz) f[j]=max(f[j],f[j-a[i].pz]+a[i].pz*a[i].wz);
if(j>=a[i].pz+a[i].b[1].pf) f[j]=max(f[j],f[j-a[i].pz-a[i].b[1].pf]+a[i].pz*a[i].wz+a[i].b[1].pf*a[i].b[1].wf);
if(j>=a[i].pz+a[i].b[1].pf+a[i].b[2].pf) f[j]=max(f[j],f[j-a[i].pz-a[i].b[1].pf-a[i].b[2].pf]+a[i].pz*a[i].wz+a[i].b[1].pf*a[i].b[1].wf+a[i].b[2].pf*a[i].b[2].wf);
}
}
}
最后记录最小的 \(f[i]\)。
int ans=-1;
for(int i=1;i<=N;i++) ans=max(ans,f[i]);
printf("%d",ans);
NO.4 总结
现在我们归纳一下动态规划题型的详细做法:
- 阶段:将问题按时间或空间划分成若干个相互联系的阶段,以便按次序求解每个阶段的最优解。
- 状态:把大的问题分解成若干个相似的子问题,每个子问称为一个状态
例如在数字金字塔问题中:把“从底层到顶点的最优值”转换成“求从底层到每个点的最优值”,这就是一个状态,我们用 \(f[x][y]\) 记录每个状态的值。 - 决策:每个阶段的状态都是由前面阶段的状态以某种方式转换而来,而这种转换需要在多种方案中做出最优的选择。
例如在数字金字塔问题中,从底层到 \((x,y)\) 的最优值是从底层到 \((x+1,y)\) 和 \((x+1,y+1)\) 的最优值中选择最大的得到的。 - 方程:当确定好解决问题的阶段、状态和决策后,将相邻两个阶段状态转移的规律用数学语言表达出来,称为状态转移方程
例如数字金字塔问题的状态转移方程:
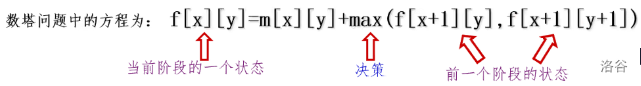
特别注意一个细节:边界条件:给出的状态转移方程是一个递推式,需要有递推开始和结束的边界条件。
其实,动态规划考的是思维,你再不会什么高深的程序命令也没关系,想通不同步骤之间是怎么转换的,一道题就迎刃而解
后记
注:文章中部分题目截图来源于学校信息学竞赛网站。

