洛谷-P8799 [蓝桥杯 2022 国 B] 齿轮-题解

洛谷链接：

• https://www.luogu.com.cn/problem/solution/P8799
• https://www.luogu.com.cn/blog/bbdxbc2-10www2022/p8799-ti-xie

这个题解主要是写给那些还没学过角速度的同学

一：齿轮比

先引入一个概念：齿轮比

\(G = \dfrac{C}{F}\)

\(G\) 为齿轮比，\(C\) 为主动齿轮齿数，\(F\) 为被动齿轮齿数。换句话说：\(C\) 代表输入齿轮齿数，\(F\) 代表输入齿轮齿数。

我们可以这样理解：若齿轮比为 \(\dfrac{36}{12}\)，化简得 \(\dfrac{3}{1}\)，说明输入齿轮转三圈，输出齿轮转一圈。

在这到题目中，由于齿轮数与周长成正比关系，而周长又与半径成正比关系。所以：

\(G = \dfrac{C_2}{C_1} = \dfrac{r_2}{r_1}\)

二：角速度

如果我们已经计算出齿轮比，且知道输入速度，则有：

\(\omega_2 = \dfrac{\omega_1}{G}\)

\(\omega_1\) 代表输入角速度，\(\omega_2\) 代表输出角速度。

角速度是什么？

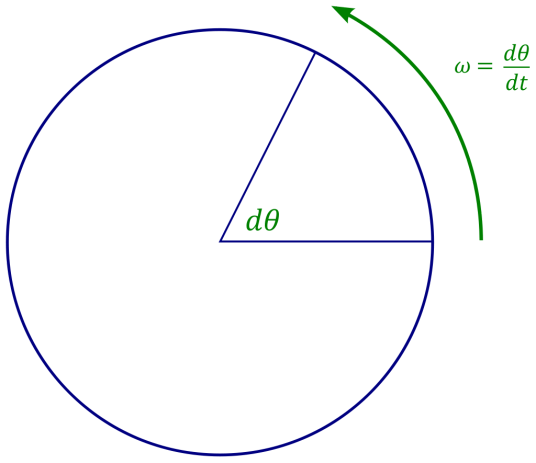
简单来讲，角速度描述了物体绕圆心运动的快慢。

三：推导

了解了前置知识，我们来看推导：

设第一个齿轮角速度为 \(\omega_1\)，半径为 \(r_1\)，第二个齿轮半径为 \(r_2\)，角速度为：

\(\omega_2 = \dfrac{\omega_1}{G} = \dfrac{\omega_1}{\frac{r_2}{r_1}} = \omega_1 \times \dfrac{r_1}{r_2}\)

那对于一串连续的齿轮，设有 \(n\) 个，则有：

\(\omega_n = \omega_1 \times \dfrac{r_1}{r_2} \times \dfrac{r_2}{r_3} \times \dfrac{r_3}{r_4} \times \cdots \times \dfrac{r_{n-1}}{r_n} = \omega_1 \times \dfrac{r_1}{r_n}\)

那对于题目中要求的 \(q\)，就可以表示了：

\(q = \dfrac{\omega_n}{\omega_1} = \dfrac{r_1}{r_n}\)

换句话说，半径与角速度成反比。

由此得出：题目要求的是在所有半径中是否有一对数比值为 \(q\)。

四：做法

• 最朴素的做法：对于每次询问，用 \(O(n^2)\) 的时间复杂度求出每对比值。至于效果嘛，自己清楚。。。
• 稍微想了一下的做法：题目已经给出 \(q\) 了，那所以开桶排，对于每一个半径 \(r_i\) 都去判断 \(r_i \times q\) 的位置上有没有另一个 \(r\)。但我亲身试过，不可以。
• \(AC\) 做法：先开一个 \(r\) 数组，记录半径，输入完排序（为了在最后判断 \(r_i \times q\) 是否大于 \(r[n]\)）。在开一个 \(vis\) 数组，桶来记录该位置上有没有 \(r\)。最后再来一个 \(ok\) 数组，记录存在的比值，以后每次询问先判断在不在 \(ok\) 里面。

五：代码

这么多大佬都发了代码，我就不贴这里了，想看的去搜记录。