搜索——优雅的暴力
(2022.12)
前言
这篇文章是在上学校竞赛课的同时结合你谷众多大神的笔记写成,一些出处都已在文章中标注。
NO.1 搜索概述
一、何为搜索?
搜索:利用计算机的高性能来有目的的穷举一个问题的所有可能或部分可能,从而求出问题的解的算法。
也就是说,搜索并不像我们想象的那么高大上,本质就是大家所爱的枚举……
当然,这里的枚举是有目的的。何谓有目的?不能瞎枚举。那么接下来请看吧。
二、搜索分类
- 深度优先搜索(DFS)
- 广度优先搜索(BFS)
NO.2 深度优先搜索
一、概述
深度优先搜索就是从问题的某种可能出发,搜索这种情况下的所有可能。当这条路不可行时,返回上一步。
蒟蒻说:我没听懂!
好吧,我说通俗一点:用一句话总结深搜:不撞南墙不回头,一定穷举完这一分支下的所有情况才罢休。
当然你也可以通过一些特殊手段减少枚举的次数,等会儿会举例。
一般来讲,深搜是一个递归的过程。如果这一分支已完成,就返回到上一次调用递归的时候。
附:深搜模板
//深度优先搜索算法框架1
int Search(int k)
{
for (i=1;i<=/*算符种数*/;i++)
if (/*满足条件*/)
{
//保存结果
if (/*到目的地*/) //输出解;
else Search(k+1);
//恢复:保存结果之前的状态{回溯一步}
}
}
//深度优先搜索算法框架2
int Search(int k)
{
if (/*到目的地*/) //输出解;
else
for (i=1;i<=算符种数;i++)
if (/*满足条件*/)
{
//保存结果;
Search(k+1)
//恢复:保存结果之前的状态{回溯一步}
}
}
(借鉴于:扬皓2006)
二、例题
(1)基础
a.方形迷宫
有一个方格迷宫,我们可以将它看作一个 \(n \times m\) 的矩阵,每个方格表示一个房间,方格中有数字 \(0\) 和 \(1\),数字 \(0\) 表示该房间是空的,可以顺利通过,数字 \(1\) 表示该房间有怪兽,不能通过。
一开始何老板位于左上角的方格(坐标 \([1,1]\) 位置),他要走到右下角的出口(坐标 \([n,m]\) 位置),每一步何老板只能往下或往右走。
他想知道总共有多少条可行的线路?
因为大家都会写递归我就不啰嗦了,重点是递归的过程。
每一步何老板只能往下或往右走! 这句话非常重要,给我们指明了递归方向。一些聪明的小朋友立马写出了:
void dfs(int i,int j){
dfs(i+1,j);
dfs(i,j+1);
}
很好,但是——忽略了两点最重要的:
- 递归何时结束?——回答:他要走到右下角的出口(坐标 \([n,m]\))
- 特殊情况?——这个递归是无止境的!碰到边界要返回。
那所以这才是正确的:
void dfs(int i,int j){
if(i==n && j==m){ans++;return;}
if(i+1<=n && map[i+1][j]!=1) dfs(i+1,j);
if(j+1<=m && map[i][j+1]!=1) dfs(i,j+1);
}
b.分数
PS:因为太懒直接上截图:
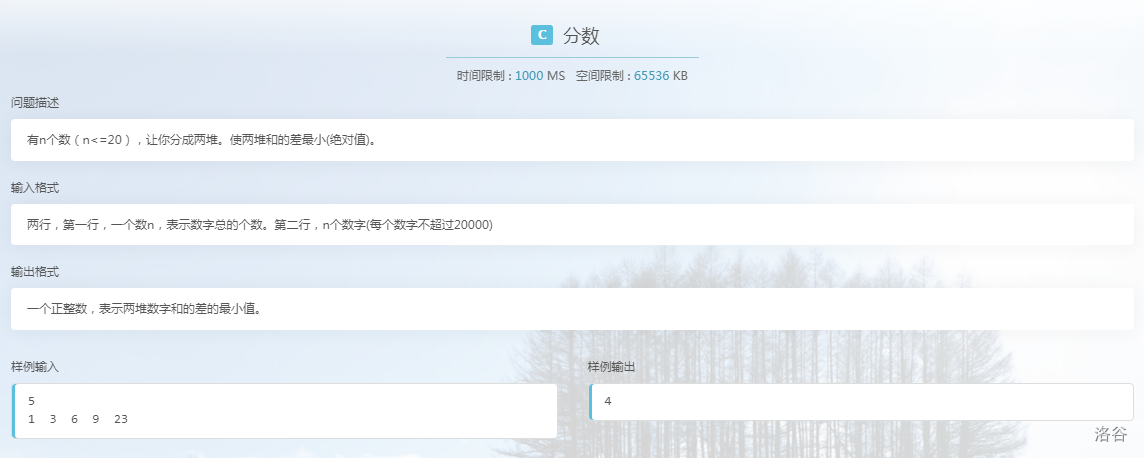
对于这道题,我们有两种思路:
第一种:(也就是例示代码)
我们在递归里面定义两个变量,一个表示第一组数字的和,另一个是第二组数字的和,例如 \(sum1\) 和 \(sum2\)。对于每个数,我们都有两种情况:
- 加到第一个数组(\(sum1+a_i\))
- 加到第二个数组(\(sum2+a_i\))
那么每一步都有两种情况,总用时为\(O(2^{20})=1048576\),肯定不会超时。
就这样一直完成 \(n\) 个数,到最后在判断 \(\left|sum1-sum2\right|\) 和 \(ans\) 的关系,最后输出。
代码:
void dfs(int now,int sum1,int sum2){
if(now>n){
if(abs(sum1-sum2)<ans) ans=abs(sum1-sum2);
return;
}
dfs(now+1,sum1+a[now],sum2);
dfs(now+1,sum1,sum2+a[now]);
}
另一种:
我们发现,把所有数相加得到 \(sumn\),另外两组数为: \(sum1\) 和 \(sum2\),差为 \(t\),可得如下等式:
\(\because sumn=sum1+sum2=sum1+(sum1+t)=2 \times sum1+t\)
\(\therefore t=sumn-2 \times sum1\)
就这个等式,我们又可以对每一步进行加入 \(sum1\) 或者不加入的选择,最后判断 \(t\) 是否比 \(ans\) 更优,也可以解决这道题。(代码自己想)
(2)进阶
a.求细胞数量
把题目简化一下,就是求连成块的数字有多少组。(块只能向上、下、左、右延伸)
我们从数据开始分析:
4 10
0234500067
1034560500
2045600671
0000000089
首先,第一个非 \(0\) 数是 \(2\) ,把 \(2\) 作为基准点,向四周扩展:
- 上?不行,超出边界;
- 左?不行,没有;
- 右?可以,递归坐标 \(i,j\) 设置为 \(1,3\);
这时,我们可以再从 \(1,3\) 开始递归,循环往复。
有两点需要注意:
- 其实我们在对此位置的上下左右进行分析时,发现一个非 \(0\) 就不必再判断另一个方位。举个例子:
2 2
23
10
当我们发现 \(2\) 的左边是 \(3\) 时,就从 \(3\) 开始了。至于 \(2\) 下面的 \(1\) 从 \(3\) 开始递归后总会途经,不必再次判断
- 每次循环后一定把当前位置设置为 \(0\) !
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
int p[505][505];
int ans=0;
void dfs(int i,int j){
if(i<1 || i>n || j<1 || j>m) return;
if(p[i+1][j]!=0){
p[i+1][j]=0;
dfs(i+1,j);
}
if(p[i-1][j]!=0){
p[i-1][j]=0;
dfs(i-1,j);
}
if(p[i][j+1]!=0){
p[i][j+1]=0;
dfs(i,j+1);
}
if(p[i][j-1]!=0){
p[i][j-1]=0;
dfs(i,j-1);
}
if(p[i+1][j]!=0){
p[i+1][j]=0;
dfs(i+1,j);
}
}
int main(){
ios::sync_with_stdio(0);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%1d",&p[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(p[i][j]!=0){
p[i][j]=1;
ans++;
dfs(i,j);
}
cout<<ans;
return 0;
}
PS.大佬们用的方向数组,我这里为了照顾萌新没用~
int tx[4]={-1,1,0,0};
int ty[4]={0,0,-1,1};
for(int i=0;i<4;i++){
x=x+tx[i];
y=y+ty[i];
}
(3)作业
(你一个蒟蒻装什么装,还布置作业。。。)
NO.3 广度优先搜索
一:概述
想要理解广度优先搜索,先从一道例题看起:
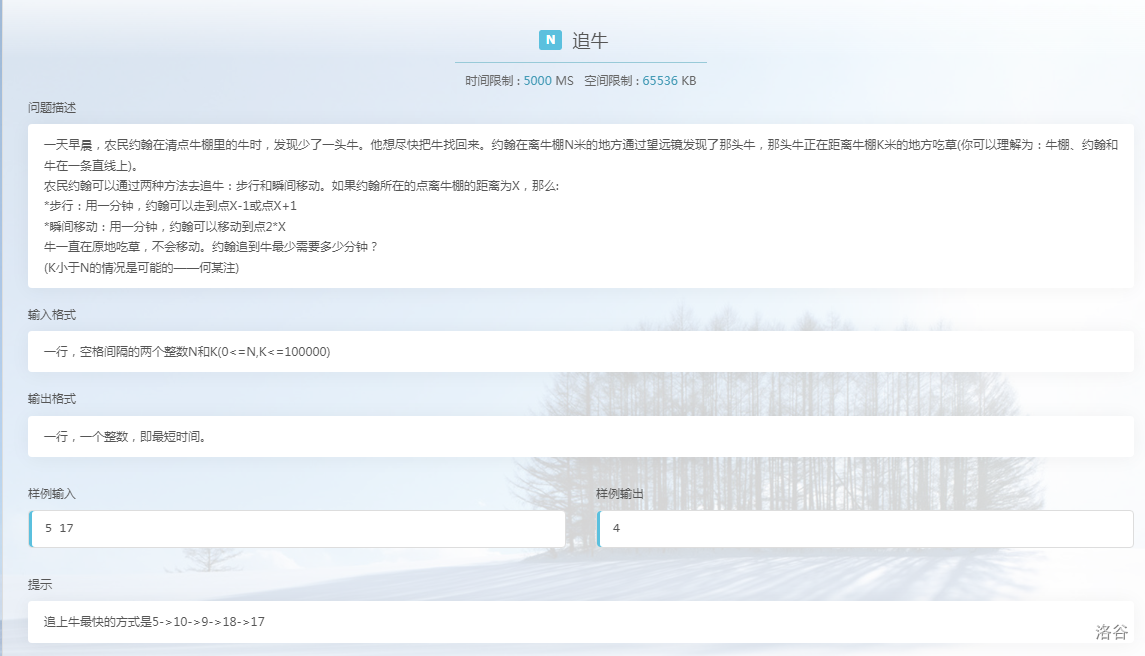
这道题大意就是说,从 \(n\) 点到 \(k\) 点最少移动几步到达。移动方式:(\(now\) 为目前位置)
- 移动到 \(now+1\);
- 移动到 \(now-1\);
- 移动到 \(now \times 2\)。
好了,你肯定又想用深搜了。但是,我用血的教训告诉你,不行!!!
而广度优先搜索,正向我们走来……
正题:广度优先搜索
广度优先搜索,又称宽度优先搜索。和深度优先搜索不同,广搜并不是一条路走到黑,而是向外一层层拓展。
我们遇到每一步,是不是下面都会有几种情况?我们每发现一个点就把这个点加入到我们的队列中,然后逐一拓展。
举个例子:
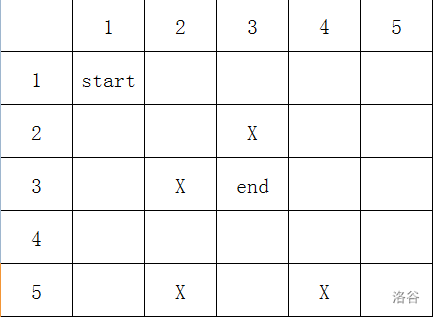
(\(X\) 表示障碍)
最开始,我们的 \(T\) 队列只有一个元素:\((1,1)\)。
我们从 \((1,1)\) 出发,有几种选择?两种。到 \((1,2)\) 或者 \((2,1)\)。那我们就把这两种加入队列:
\(T:(1,1);(1,2);(2,1)\)
(注意:每次添加结束后都要把队首元素删除,这里为了更好地演示没有删除。)
如图:

那下一步呢?\((3,1);(2,2);(1,3)\),那就加入队列:
\(T:(1,1);(1,2);(2,1);(3,1);(2,2);(1,3)\)
如图:
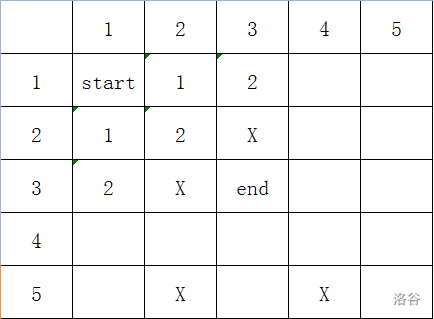
最后:
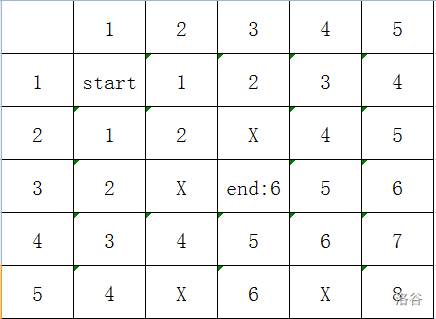
就这样,一直把下一步添加到队列里面,如果当某一步到达终点,就结束。
附:广度优先搜索模板:
void bfs(){
/*定义队列*/ q;
q.push(/*初始状态*/);
while(/*队不空*/){
x(y)=/*队头状态信息*/;
/*出队*/;
if(/*下一步可行*/)下一步;
}
}
借鉴于:Aw顿顿
二、例题
(1)刚刚的引子
我们先把刚刚的引子解决了来。按照思路,先梳理几个要点:
-
队列:简单,大家都会
-
每一步的拓展:对于这道题,有几种情况:
- 移动到 \(now+1\);
- 移动到 \(now-1\);
- 移动到 \(now \times 2\)。
对于每一种情况,我们先要判断将要入队的点位置是否已经走过(这叫“剪枝”,后面会讲),若没有,就入队并标记此位置。
-
输出:专门弄一个数组,储存到每一点所需要的步数,最后输出第 \(k\) 点即可。
代码已备好:
void bfs(){
t.push(n);//t为队列
p[n]=false;//p数组用来记录是否已经到达过。
while(!t.empty()){
if(ans==k) break;
ans=t.front();
t.pop();
if(ans+1<=100005 && !p[ans+1]){
t.push(ans+1);
p[ans+1]=true;
coutt[ans+1]=coutt[ans]+1;//输出数组
}
if(ans-1>=0 && !p[ans-1]){
t.push(ans-1);
p[ans-1]=true;
coutt[ans-1]=coutt[ans]+1;
}
if(ans*2<=100005 && !p[ans*2]){
t.push(ans*2);
p[ans*2]=true;
coutt[ans*2]=coutt[ans]+1;
}
}
}
(2)好人何老板
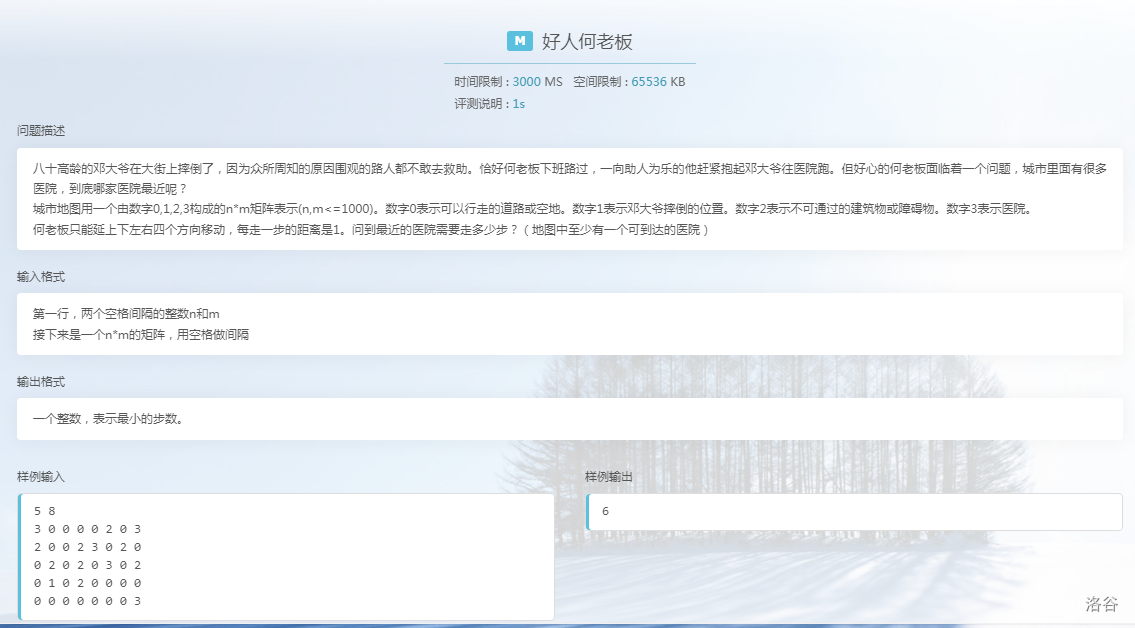
这道题其实是之前说 dfs 讲的题的进阶版,如果我们还用 dfs 去做,时间就会超,这里我们不用 \(STL\) 去做,来一波手工队列!
#include<bits/stdc++.h>
using namespace std;
struct node{
int x,y,step;
};
node q[1005*1005],start;
int n,m;
int a[1005][1005],head,tail,tx,ty;
int dx[4]={-1,1,0,0};
int dy[4]={0,0,-1,1};
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
if(a[i][j]==1){
start.x=i;
start.y=j;
}
}
head=1;tail=2;
q[head].x=start.x;q[head].y=start.y;q[head].step=0;
a[start.x][start.y]=2;
while(true){
for(int i=0;i<4;i++){
tx=q[head].x+dx[i];
ty=q[head].y+dy[i];
if((tx>0)&&(tx<=n)&&(ty>0)&&(ty<=m)&&(a[tx][ty]!=2))
{
//cout<<tx<<" "<<ty<<endl;
if(a[tx][ty]==3){
printf("%d",q[head].step+1);
return 0;
}
q[tail].x=tx;q[tail].y=ty;
q[tail].step=q[head].step+1;
a[tx][ty]=2;
tail++;
}
}
head++;
}
return 0;
}
NO.4 搜索剪枝
一、剪枝概述

请看上图,简单来说,搜索剪枝就是通过某种方式减少枚举量,已达到时间更少的目的。
二、例题
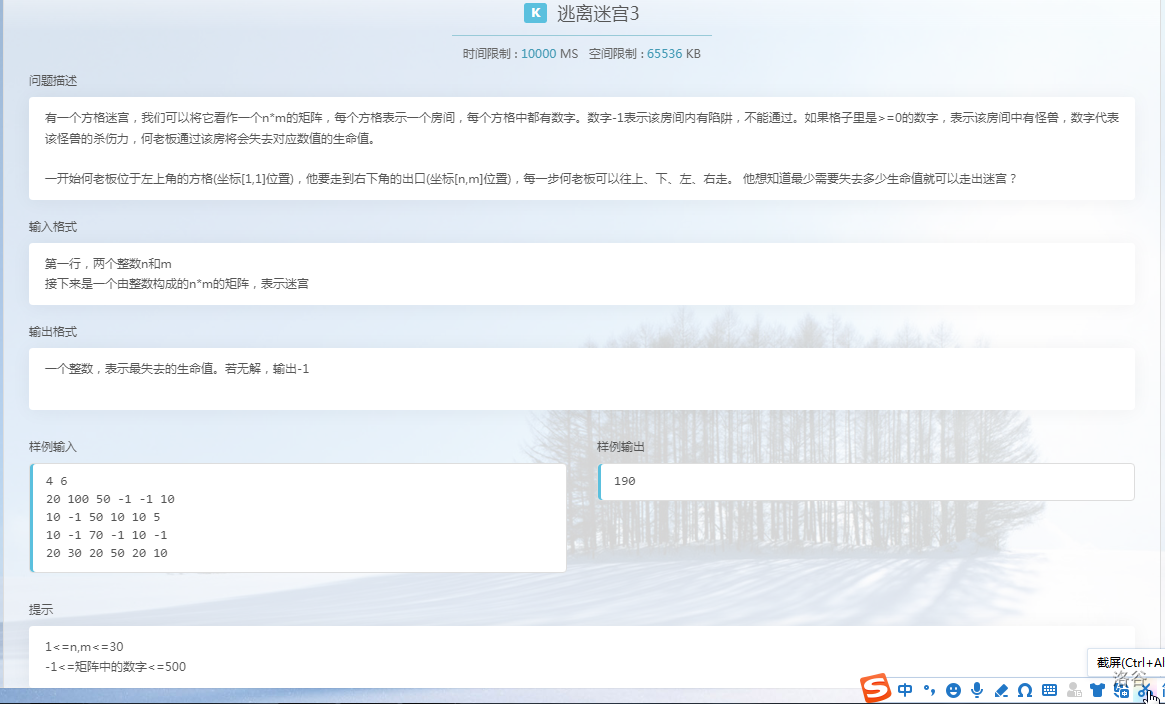
这道题按常规做法肯定要超时,我们需要一些手段让其将减少枚举量。
这是原来代码:
void dfs(int i,int j,int js){
js+=bbd[i][j];
if(i==n && j==m){
ans=min(ans,js);
return;
}
if(i+1<=n) dfs(i+1,j,js);
if(i-1>=1) dfs(i-1,j,js);
if(j+1<=m) dfs(i,j+1,js);
if(j-1>=1) dfs(i,j-1,js);
}
第一:我们的 \(js\) 有没有优化的空间?
因为我们想要求的是最小的 \(js\),那所以当走到某一步时 \(js > ans\) 时就可以不再枚举下去了,因为无论再怎么走肯定都不能让 \(js\) 更小。
由此写出优化一:
void dfs(int i,int j,int js){
js+=bbd[i][j];
if(js>ans) return;
if(i==n && j==m){
ans=min(ans,js);
return;
}
if(i+1<=n && bbd[i+1][j]!=-1) dfs(i+1,j,js);
if(i-1>=1 && bbd[i-1][j]!=-1) dfs(i-1,j,js);
if(j+1<=m && bbd[i][j+1]!=-1) dfs(i,j+1,js);
if(j-1>=1 && bbd[i][j-1]!=-1) dfs(i,j-1,js);
}
第二:我们在递归时是否存在“原地打转”的情况?
这是有可能的,因为我们并没有记录我们曾经到过的地方。所以,想出优化方案:
- 当到达一点时,将这一点数值标为 \(-1\),以后递归时判断此点数值是否为 \(-1\),如果是就不在从这个位置往下深搜。
- 在这种路径全部结束后再把这个点变回原来数值。
由此写出优化二:
void dfs(int i,int j,int js){
js+=bbd[i][j];
if(i==n && j==m){
ans=min(ans,js);
return;
}
if(js>ans) return;
int t=bbd[i][j];//保存值,不然没了
bbd[i][j]=-1;
if(i+1<=n && bbd[i+1][j]!=-1) dfs(i+1,j,js);
if(i-1>=1 && bbd[i-1][j]!=-1) dfs(i-1,j,js);
if(j+1<=m && bbd[i][j+1]!=-1) dfs(i,j+1,js);
if(j-1>=1 && bbd[i][j-1]!=-1) dfs(i,j-1,js);
bbd[i][j]=t;
}
第三:最优化剪枝
我们有时可以不必在 \(js > ans\) 时在做判断。如果此时到终点最好的方案都比 \(ans\) 大,那就可以跳出了。
在此题中,我们可以用 \(min\) 来记录地图上每个位置的最小值,最短路径(\(n-i+m-j\))与 \(min\) 的乘积在加上 \(js\) 如果都大于 \(ans\) 就可以跳出了。
优化三:
void dfs(int i,int j,int js){
js+=bbd[i][j];
if(i==n && j==m){
ans=min(ans,js);
return;
}
if(js>ans) return;
if(js+(n-i+m-j)*min>ans) return;//在这里!
int t=bbd[i][j];
bbd[i][j]=-1;
if(i+1<=n && bbd[i+1][j]!=-1) dfs(i+1,j,js);
if(i-1>=1 && bbd[i-1][j]!=-1) dfs(i-1,j,js);
if(j+1<=m && bbd[i][j+1]!=-1) dfs(i,j+1,js);
if(j-1>=1 && bbd[i][j-1]!=-1) dfs(i,j-1,js);
bbd[i][j]=t;
}
第四:记忆化
还可以怎么优化呢?当到达一个点时,我们记录下到达这个点所需要的最小 \(js\) 是什么,以后无论怎么深搜,如果发现此时的 \(js\) 大于之前所记录的,就直接跳出。当然了,我们需要另一个数组来记录。
优化四:
void dfs(int i,int j,int js){
js+=bbd[i][j];
if(js<cost[i][j]) cost[i][j]=js;//找最小值
else return;//返回
if(i==n && j==m){
ans=min(ans,js);
return;
}
if(js>ans) return;
if(js+(n-i+m-j)*min>ans) return;
int t=bbd[i][j];
bbd[i][j]=-1;
if(i+1<=n && bbd[i+1][j]!=-1) dfs(i+1,j,js);
if(i-1>=1 && bbd[i-1][j]!=-1) dfs(i-1,j,js);
if(j+1<=m && bbd[i][j+1]!=-1) dfs(i,j+1,js);
if(j-1>=1 && bbd[i][j-1]!=-1) dfs(i,j-1,js);
bbd[i][j]=t;
}
(这里的 \(cost\) 数组需要赋初值哟,自己想吧~)
总结:

(完结)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号