题目

考虑在一个打印机上整齐地打印一段文章的问题。输入的正文是n个长度分别为L1、L2、……、Ln（以字符个数度量）的字符构成的序列。我们希望将这个段落在一些行上整齐地打印出来，每行至多M个字符。“整齐度”的标准如下：如果某一行包含从i到j的单词（i<j），且单词之间只留一个空格，则在行末多余的空格字符个数为 ，它必须是非负值才能让该行容纳这些单词。我们希望所有行（除最后一行）的行末多余空格字符个数的立方和最小。请给出一个动态规划的算法，来在打印机整齐地打印一段又n个单词的文章。分析所给算法的执行时间和空间需求。

解题

如果某一行包含从i到j的单词（i<j），且单词之间只留一个空格，则在行末多余的空格字符个数为 

 

 

该行的单词数：j-i + 1 

该行单词的总长度：

 

该行单词见的空格数：j - i 

 

可以发现：单词的总长度 + 单词间的空格 + 该行末尾空格数 = M  M就是改行允许最多字符的长度

 

所有上面所谓的行末尾空格字符的个数是根据前面单词个数决定的，而不是后面空格数量决定前面单词个数的，当该行能够放单词就可以继续放，但是长度不能够超过M

其中A表示单词长度的数组，A[i]表示 i 单词的长度 

可以先求出可以放单词所有的组合末尾空格数量的立方的矩阵W 

W[i][j] 表示从单词 i 到单词 j 形成的行的末尾空格数量的立方，其中 i<=j  

定义-1作为标准位表示i 到 j 内的单词 不可以在一行

        int [][] W = new int[len][len]; // W[i][j] 表示 i 到 j 单词所在行的末尾空格数

        for(int i=0;i< len;i++){
            for(int j=i;j<len;j++){// 只保存上三角元素
                int w = M - j + i;
                for(int k = i;k<=j;k++){
                    w -=A[k];
                }
                w = (int) Math.pow(w, 3);
                if(w<0)
                    w = -1;// 标志为 不可以 形成第i单词 到 第j单词的行，用 -1 作为标志位
                W[i][j] = w;    
            }
        }

如何根据动态规划进行解题？

先找到子问题：

对于数字A，元素表示单词的长度

题目现在每行最长是M，每行元素尽量的填满，每行字符长度小于等于M，这样可以使得行的数量尽量的少，和每行的空格数量尽量的少，可以使得最后的空格立方和尽量的小

定义数组B，B[i]表示0---i单词的排列使得末尾空格立方和最小的值

所有

 

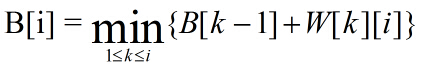
初始值：

B[0] = W[0][0]

在遍历的时候要过滤掉-1的情况，否则会出错，之间找到 0 当然是最小的了。

对应程序

        B[0] =W[0][0];
        for(int i = 1;i<len;i++){
            B[i] =  Integer.MAX_VALUE;
            for(int k = 1;k<=i;k++){
                if(W[k][i]!=-1){
                    B[i] = Math.min(B[i], B[k-1] + W[k][i]);
                }
                
            }
            
        }

 

测试

int[] A = new int[]{4,3,2,6,4,2,3,6};
int M = 8;

 

输出结果

64    0    -1    -1    -1    -1    -1    -1    
     125    8    -1    -1    -1    -1    -1    
          216    -1    -1    -1    -1    -1    
                  8    -1    -1    -1    -1    
                        64    1    -1    -1    
                             216    8    -1    
                                  125    -1    
                                         8    
=======================================
160

上面输出的矩阵就是W矩阵

根据W矩阵如何选取合适的值？

选取非负数

这里选取的标准和N皇后问题有点类似，元素不同行不同列，这里有一个稀疏的显著：相邻元素之间可以不选取，还有一个限制就是W[i][j]元素下一个元素W[i+1][j]所在的行i+1不能取

上面红色字体之和就是160，就是程序输出的答案

如何输出每行的元素？

只需要找到元素的分割点就好了

按照下面找切分点不正确

for(int i = 1;i<len;i++){
            B[i] =  Integer.MAX_VALUE;
            for(int k = 1;k<=i;k++){
                if(W[k][i]!=-1){
                    B[i] = Math.min(B[i],B[k-1] + W[k][i] );
                    if(B[i] == B[k-1] + W[k][i])
                        C[i] = k;
                }
                
            }
            
        }
        for(Integer c:C){
            System.out.print(c+"\t");
        }
View Code

全部程序

package dp;

public class PrintNeatly {
    /**
     * 
     * @param A A[i]表示第i个字符的长度
     * @param M 每行最多字符个数
     * @return
     */
    public int getNeatly(int[] A,int M){
        int len = A.length;
        int [][] W = new int[len][len]; // W[i][j] 表示 i 到 j 单词所在行的末尾空格数
        int [] B = new int[len];// B[i] 表示 0 到i内单词最优空格立方总和
        int [] C = new int[len];// C[i] 表示每行的开始位置
        for(int i=0;i< len;i++){
            for(int j=i;j<len;j++){// 只保存上三角元素
                int w = M - j + i;
                for(int k = i;k<=j;k++){
                    w -=A[k];
                }
                w = (int) Math.pow(w, 3);
                if(w<0)
                    w = -1;// 标志为 不可以 形成第i单词 到 第j单词的行，用 -1 作为标志位
                W[i][j] = w;    
            }
        }
        for(int i=0;i<len;i++){
            for(int j=0;j<len;j++){
                if(j>=i)
                    System.out.print(W[i][j]+"\t");
                else
                    System.out.print(" "+"\t");
            }
            System.out.println();
        }
        
        B[0] =W[0][0];
        for(int i = 1;i<len;i++){
            B[i] =  Integer.MAX_VALUE;
            for(int k = 1;k<=i;k++){
                if(W[k][i]!=-1){
                    B[i] = Math.min(B[i],B[k-1] + W[k][i] );
                    if(B[i] == B[k-1] + W[k][i])
                        C[i] = k;
                }
                
            }
            
        }
        for(Integer c:C){
            System.out.print(c+"\t");
        }
        return B[len-1];
    }
    public static void main(String[] args){
        PrintNeatly pN = new PrintNeatly();
    
        int[] A = new int[]{4,3,2,6,4,2,3,6};
        int M = 8;
        int result = pN.getNeatly(A, M);
        System.out.println("=======================================");
        System.out.println(result);
    }
}
View Code