题目描述

 

有一组砝码，重量互不相等，分别为m1、m2、m3……mn；它们可取的最大数量分别为x1、x2、x3……xn。
现要用这些砝码去称物体的重量,问能称出多少种不同的重量。
现在给你两个正整数列表w和n， 列表w中的第i个元素w[i]表示第i个砝码的重量，列表n的第i个元素n[i]表示砝码i的最大数量。  i从0开始                   
请你输出不同重量的种数。
如：w=[1,2], n=[2,1], 则输出5（分析：共有五种重量：0,1,2,3,4）

 

解题

参考智力题砝码称重问题，有一个这样的样例：砝码重量：[1,3,9],个数：[1,1,1]可以称出1到13内的质量

然后自己死活写不出来，网上整理了砝码称重的智力题，又发现说这个是背包问题，就做了背包问题相关题目

PythonTip解题报告中给了下面的程序：

 

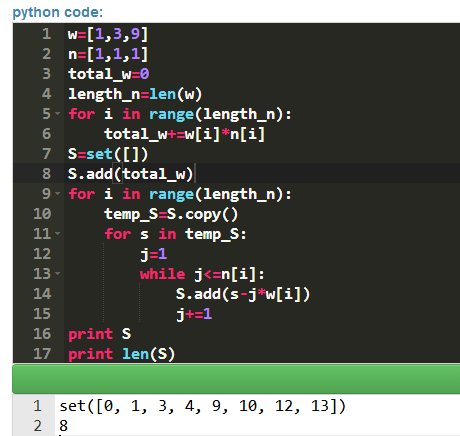
根据输出结果可以看出：本题的砝码称重，砝码必须放在同一侧，砝码一侧，重物一侧。在上面的测试环境中可以通过，网上看到的砝码称重大部分就是这样的称重

上面程序的原理：

定义集合set：表示能够称出的重物重量

set初始化:所有砝码的重量

 遍历所有种类的砝码：

遍历该种类砝码的数量：

可以称出新的重物质量 = 集合内的值 减去 砝码的重量*砝码的个数

循环结束后集合内的值就是答案了

   根据果壳 中的讲解，可以发现上面的过程没有 -a 的情况，只有 0 a的情况，也就是说砝码必须都放在同一侧

 初始集合值是0：

length_n=len(w)
S=set([])
S.add(0)
for i in range(length_n):
    temp_S=S.copy()
    for s in temp_S:
        j=1
        while j<=n[i]:
            S.add(s+j*w[i])
            j+=1
#print S 
print len(S)

Java

    public int backPack2(int[]A,int []B){
        int total = 0;
        for(int i=0;i<A.length;i++)
            total +=A[i]*B[i];
        TreeSet<Integer> set = new TreeSet<Integer>();
        set.add(total);
        for(int i=0;i<A.length;i++){
            Object[] setCopy = set.toArray();
            for(Object s:setCopy){
                int j = 1;
                while(j<=B[i]){
                    set.add(((Integer)s-j*A[i]));
                    j++;
                }
            }
        }
        for(Integer s:set){
            System.out.print(s+" ");
        }
        return set.size();
    }

下面考虑砝码可以放在天平的不同侧的情况

参考：http://www.tuicool.com/articles/yqYjM3

讲解见注释

    /**
     * A[i] 第i个砝码的重量
     * B[i] 第i个砝码的数量
     * @param A
     * @param B
     * @return
     */
    public int backPack3(int[]A,int []B){
        int total = 0;
        for(int i=0;i<A.length;i++)
            total +=A[i]*B[i];
        boolean dp[] = new boolean[total+1]; // dp[i] = true 表示可以称出质量为 i 的重物 
        dp[0] = true; 
        for(int i=0;i<A.length;i++){// 砝码重量
            for(int j = 0;j<=B[i];j++){// 对 第 i个砝码遍历其种类
                for(int s=total;s>=A[i];s--){ // 砝码的总重量开始遍历，为什么？ total -- A[i] 的质量是否能够称出 能否称出体现着 s-A[i]能否称出
                    if(dp[s - A[i]]) // dp[s - A[i]] = true 就是可以称出 s - A[i]的重物，也就是可以称出 s - A[i] + A[i] 的重物 
                        dp[s] = true;
                }
            }
        }
        int count = 0;
        for(int i = 0;i<total+1;i++){
            if(dp[i]){
                System.out.print(i+" ");
                count++;
            }
        }
        return count;
    }