堆
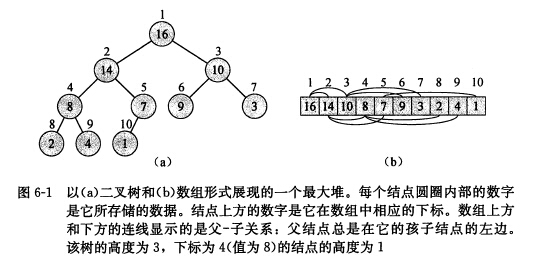
堆是一个数组,它可以被看成一个近似的完全二叉树,树上的每一个结点对应数组中的一个元素。除去最底层外,该树是完全充满的,而且从左到右填充。
用数组A表示堆,从数组第1个元素开始,数组中第i(1<=i <=n)个元素,其父结点,左孩子,右孩子的下标如下
// 父结点 public int parent( int i){ return i/2; } // 左孩子 public int left(int i){ return 2*i; } // 右孩子 public int right(int i){ return 2*i+1; }
当数组起始下标是0的时候,其父结点,左右孩子结点如下
// 父结点 public int parent( int i){ return (i-1)/2; } // 左孩子 public int left(int i){ return 2*i+1; } // 右孩子 public int right(int i){ return 2*i+2; }
堆可以分为大顶堆和小顶堆
大顶堆:结点 i 的值 都大于其左右孩子结点的值
小顶堆:结点 i 的值 都小于其左右孩子结点的值
二叉树的形式与数组形式表达堆之间元素的关系
练习1,高度为h的堆,元素最少和最多是多少?
最多:这个完全二叉树第h层元素填满:2^h - 1
最少:第h-1层填满,第h层只有一个元素:2^(h-1) -1 + 1 = 2^(h-1)
说明:h=1 表示第一层
练习2,含有n个元素的堆的高度是 [lgn]
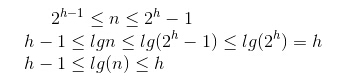
练习3,当用数组存放堆的时候,堆的元素时候n,求叶子结点下标

构建大顶堆
max-heapify 用于维护一个大顶堆。它的输入是一个数组A和下标i。在调用max-heapify的时候,假定根结点left(i) 和right(i) 的二叉树都是大顶堆,但这时A[i]有可能小于其中的一个孩子,这样就违背大顶堆的性质。我们需要进行调整,选取left(i) right(i) 对应结点较大的一个和 i 位置处的结点进行互换。
建堆代码如下
/** * 调整堆元素 * @param A * @param n * @param i */ public void max_heapify(int[] A ,int n,int i){ // 左孩子结点 int l = left(i); // 右孩子结点 int r = right(i); // 最大结点下标 int largest = -1; // 与左孩子判断 if(l<= n && A[l] > A[i]) largest = l; else largest = i; // 与右孩子判断 if(r <=n && A[r] > A[largest]) largest = r; // i 结点不是最大值maxId 和i 结点进行交换 if(largest != i ){ swap(A,largest,i); max_heapify(A,n,largest); } } /** * 交换 * @param A * @param l * @param r */ public void swap(int [] A,int l,int r){ int tmp = A[l]; A[l] = A[r]; A[r] = tmp; }
时间复杂度:O(lg(n))
说明:
在 i left(i) right(i) 三个结点中,选取其对应的值最大的结点和 i 结点的值进行交换。在交换后,下标为largest的结点的值是原来的A[i] 的值,largest所在的结点的子树可能违反大顶堆的性质,需要对该子树递归调用max-heapify
这里的假设是 以left(i) right(i) 为结点的堆已经是大顶堆,所以这个时候,我们只需要上面的三个元素就好了
算法导论例子

改成循环代码
/** * 调整堆元素 * @param A 数组存放堆 * @param n 数组的数量 从 1 - n 开始 * @param i 需要调整的堆 元素 位置 */ public void max_heapify1(int[] A ,int n,int i){ int l = -1; int r = -1; int largest = -1; while(true){ l = left(i); r = right(i); if(l<=n && A[l] > A[i]) largest = l; else largest = i; if(r <=n && A[r] > A[largest]) largest = r; if(largest!=i){ swap(A,largest,i); //更新i 的值相当的递归调用 i = largest; // 相等 对左右子树不影响 }else{ break; } } }
建堆
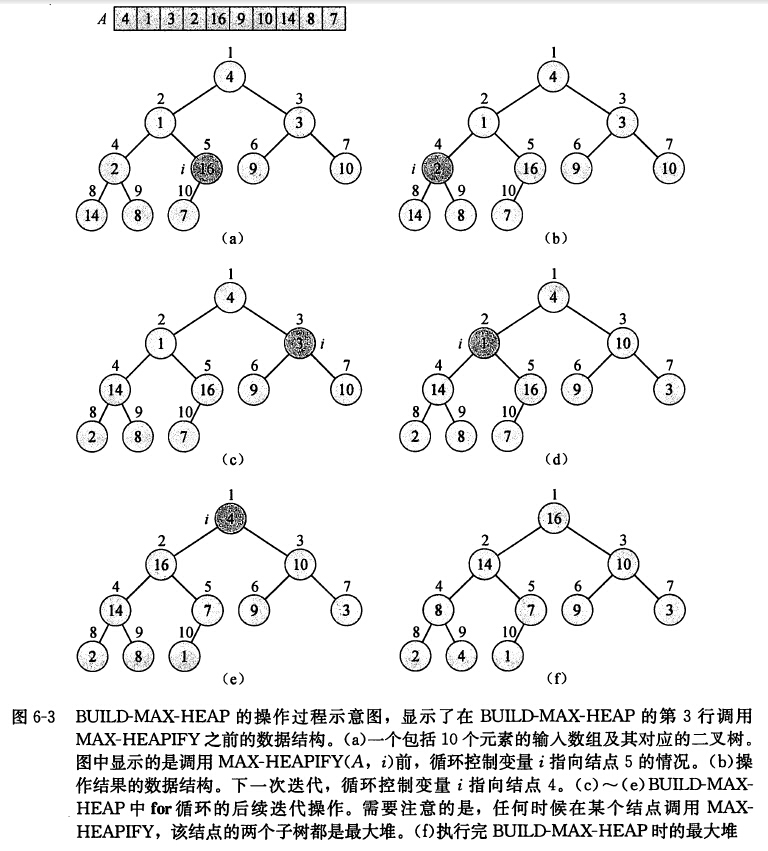
自底向上的方法,利用max-heapify 把一个大小为n 的数组A[1,...,n] 转换成大顶堆。子数组A[[n/2] +1,...,n] 中的元素是树的叶子结点。每个叶子结点可以看成一个大顶堆,所有在建堆的时候从 n/2 的元素开始 一直到 第 1 的元素。
为什么这样做?因为对当前结点进行操作时能够保证以当前结点为根的树的子树都已经是最大顶堆。这是从后像前的过程,先把底层的大顶堆构建好,再逐步的构建上层的大顶堆,在一定程度上减少了不比较的操作。如果是从1 到 n/2 的时候,对于新加入的元素,前面已经构建好的大顶堆可能都需要进行更新。比如,我们已经在第100层, 新插入的元素比之前堆内的元素都大,如100000,前面已经构建好的99层都要进行调整。
/** * 建立大顶堆 * @param A * @param n */ public void build_max_heap(int[] A,int n){ for(int i = n/2;i>=1;i--){ max_heapify(A,n,i); } }
时间复杂度:O(nlog(n))
算法导论建堆例子
堆排序算法
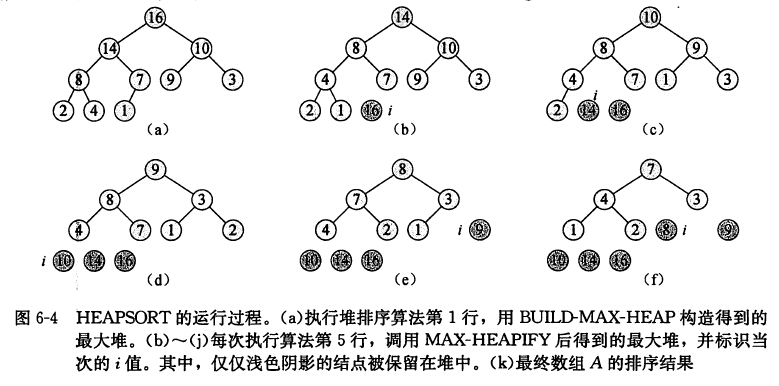
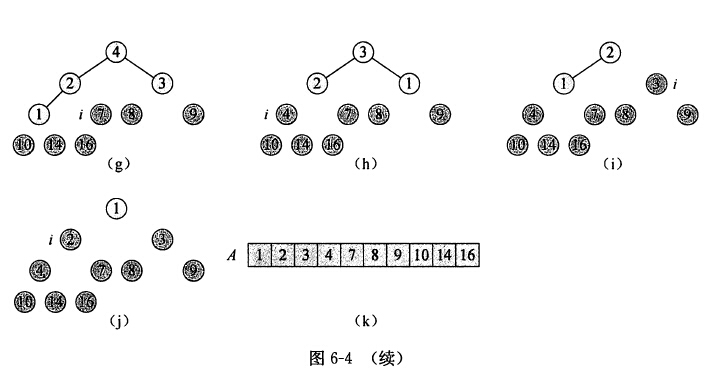
初始时候,利用build_max_heap将输入数组A[1,..,n] 建成大顶堆,这里A[1]一定是最大的元素,将A[1]与A[n]互换,再对A[1,...,n-1] 调整为大顶堆,然后A[1]与A[n-1]元素互换,再对A[1,...,n-2] 调整为大顶堆,如此循环下去
/** * 堆排序 升序 * @param A * @param n */ public void heap_sort(int[] A,int n){ build_max_heap(A,n); for(int i = n;i>=2;i--){ swap(A,i,1); max_heapify(A,i-1,1); } }
堆排序的时间复杂度:O(nlogn)
算法导论例子
所有程序

package heapSort; class heap{ /** * 堆排序 升序 * @param A * @param n */ public void heap_sort(int[] A,int n){ build_max_heap(A,n); for(int i = n;i>=2;i--){ swap(A,i,1); max_heapify(A,i-1,1); } } /** * 建立大顶堆 * @param A * @param n */ public void build_max_heap(int[] A,int n){ for(int i = n/2;i>=1;i--){ max_heapify(A,n,i); } } /** * 调整堆元素 * @param A 数组存放堆 * @param n 数组的数量 从 1 - n 开始 * @param i 需要调整的堆 元素 位置 */ public void max_heapify1(int[] A ,int n,int i){ int l = -1; int r = -1; int largest = -1; while(true){ l = left(i); r = right(i); if(l<=n && A[l] > A[i]) largest = l; else largest = i; if(r <=n && A[r] > A[largest]) largest = r; if(largest!=i){ swap(A,largest,i); //更新i 的值相当的递归调用 i = largest; // 相等 对左右子树不影响 }else{ break; } } } /** * 调整堆元素 * @param A * @param n * @param i */ public void max_heapify(int[] A ,int n,int i){ // 左孩子结点 int l = left(i); // 右孩子结点 int r = right(i); // 最大结点下标 int largest = -1; // 与左孩子判断 if(l<= n && A[l] > A[i]) largest = l; else largest = i; // 与右孩子判断 if(r <=n && A[r] > A[largest]) largest = r; // i 结点不是最大值maxId 和i 结点进行交换 if(largest != i ){ swap(A,largest,i); max_heapify(A,n,largest); } } /** * 交换 * @param A * @param l * @param r */ public void swap(int [] A,int l,int r){ int tmp = A[l]; A[l] = A[r]; A[r] = tmp; } // 父结点 public int parent( int i){ return i/2; } // 左孩子 public int left(int i){ return 2*i; } // 右孩子 public int right(int i){ return 2*i+1; } } public class heapSort { public static void main(String[] args) { heap h = new heap(); // 第一个元素不考虑 int[] A = new int[]{-1,4,1,3,2,16,9,10,14,8,7}; int n = A.length-1; //h.build_max_heap(A, n); //printA(A); //16 14 10 8 7 9 3 2 4 1 //16 14 10 8 7 9 3 2 4 1 h.heap_sort(A, n); System.out.println(); printA(A); } public static void printA(int[] A){ for(int i:A){ System.out.print(i+" "); } } }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号