Andrew Ng 深度学习笔记-01-week2-课程

一、专业词汇：

neural  network programming     神经网络编程

implement a neural network       构建神经网络

forward pass/forward propagation step   正向传播

backward pass/backword propagation step 反向传播

logistics regression     logistic回归

binary classification     二分分类

dimension  维度

input  feature  vector  输入的特征向量

classifier    分类器

training sets  训练集

training examples  训练样本

transpose   转置

matrix   矩阵    vector 向量 

supervised learning 监督学习

gradient descent algorithm 梯度下降法

the global optimum  全局最优解

 calculus  微积分

derivatives 导数

slope 斜率

vectorization 向量化

scaleable deep learning 可扩展深度学习

graphics processing unit  GPU  图像处理单元  CPU和GPU均有并行化的指令 统称SIMD，即 single  instruction multiple data  单指令流多数据流

 parallelization   instructions    并行化指令

二、编程技巧：

尽量不要直接使用for循环，可能存在数量巨大的数据集，建议使用向量化技术，即使用向量化技术摆脱for循环

X.shape  输出矩阵X的维度

由于都是计算的J对其他变量的导数，所以用dw表示dJ对w的导数

 Z=np.dot(W,x)  通过向量化计算W*x

 类似的np. 即Python中的numpy能够充分利用并行化：np.exp(v)  np.log(v)  np.maximum(v,0) .......

 u=np.zeros((n,1))  生成n个包含一个元素0的矩阵

 cal=A.sum(axis=0)   代表将A矩阵中的元素进行竖直相加   如果是水平轴，则axis=1

 在编写时，当不完全确定是什么矩阵、不确定矩阵的尺寸时，使用reshape，确保其是正确的列向量或行向量

广播的应用：

一个列向量+一个数，python会自动把实数扩展为相应的列向量（进行相应的水平复制或者垂直复制）：

例如：

 

 编程时容易出现的错误：

尽量不使用秩为1的数组a（既不是行向量，也不是列向量，a=a的转置，a和a的转置的内积是一个数）

应使用如下类似的矩阵：（将（n,1）看做列向量，（1,n）看做行向量）

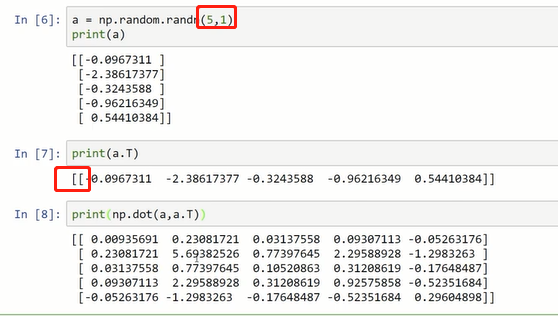
编写时可以加类似如下的声明：

 

当发现了秩为1的数组时，可以使用reshape将其转化为向量：

a=a.reshape((5,1))

三、思维：

logistic回归：用于二分分类的算法

例子：用y表示一个预测的图片中是不是包含猫，y表示结果，1表示是，0表示不是

          例如用一个X表示一个图片亮度的像素值，假如是64*64，则X的维度为：64*64*3  

二分分类问题中，目标是训练一个分类器，这个分类器 以图片的特征向量x作为输入，输出结果y（0或1）

训练样本（i）对应的预测值是y^(i)

 其中的w、x都是n维列向量：

 

loss函数作用于单个样本

cost函数J（w，b）作用于整个训练集

需要找到更合适的w，b 使得cost函数尽可能小

需要使用初始值初始化w和b ，对于logistic 回归而言，几乎任意的初始化方法都有效，虽然一般会进行初始化为0的操作，但在此不进行这样的初始化

梯度下降法的做法：从初始点开始，朝着最陡的下坡方向走，经过多次迭代，最终收敛到全局的最优解

 先忽略b，做w的图像：

 

学习率控制每一次的迭代

在w函数的右侧，导数是正的，w不断减少，在左边，导数是负的，w不断增加

 函数的导数即为函数的斜率，一次函数中为高/宽，其他函数在每个不同的点，斜率不一样，参考微积分对应的公式进行求导/求斜率

使用流程图，求更加复杂的函数的导数：

 正向传播计算正常的J：（从左到右计算成本函数）

假设样本有两个特征，x1和x2

在logistic回归中，我们要做的是：通过变换参数w和b的值，使loss函数最小化

 

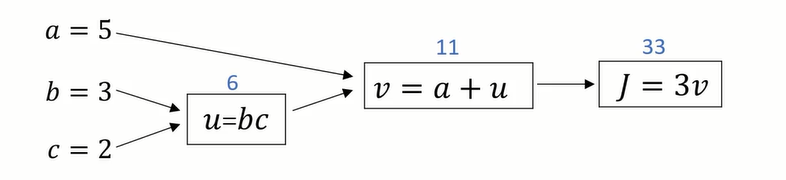
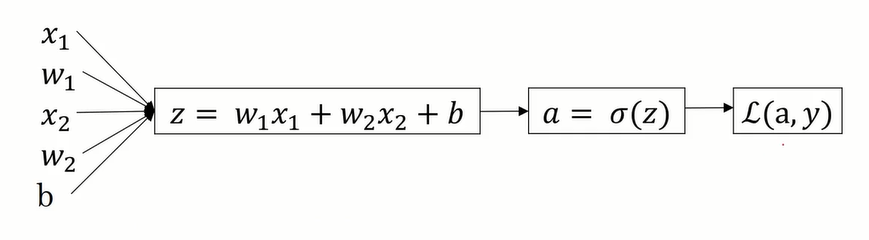
反向传播计算导数：

 

 

m个样本的logistic回归（对logistic回归应用梯度下降法，实现梯度下降法的迭代）：

一次梯度下降：

 

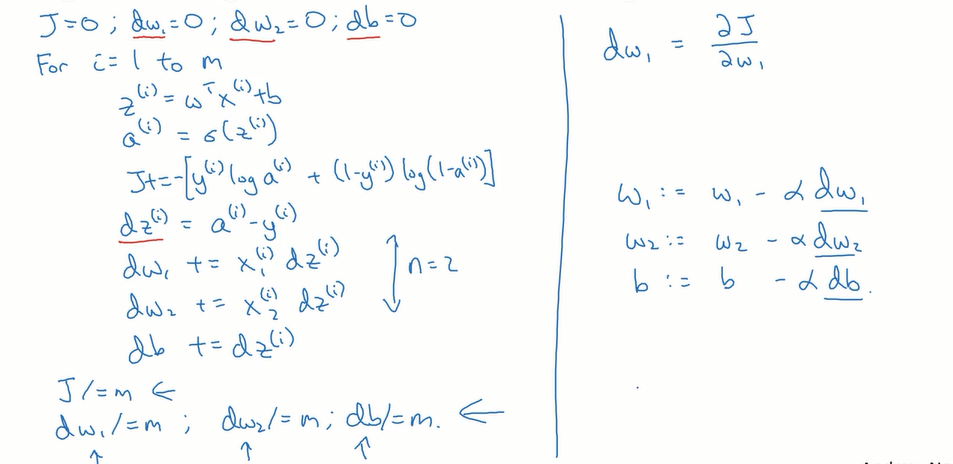
在此包含两个for循环，一个用来遍历m个训练样本，一个用来遍历所有的特征

向量化：

for循环和向量化的对比：

 

 向量化的例子：

矩阵和向量相乘，for循环与np.dot()比较

 

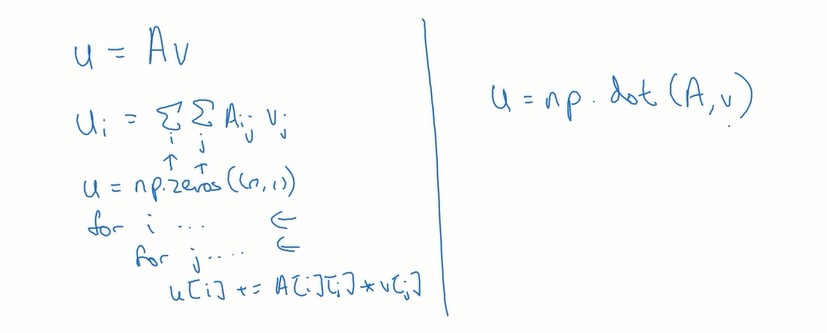
做指数运算，应该用numpy里面的内置函数代替for循环：

只剩一次for循环的多次梯度下降迭代：

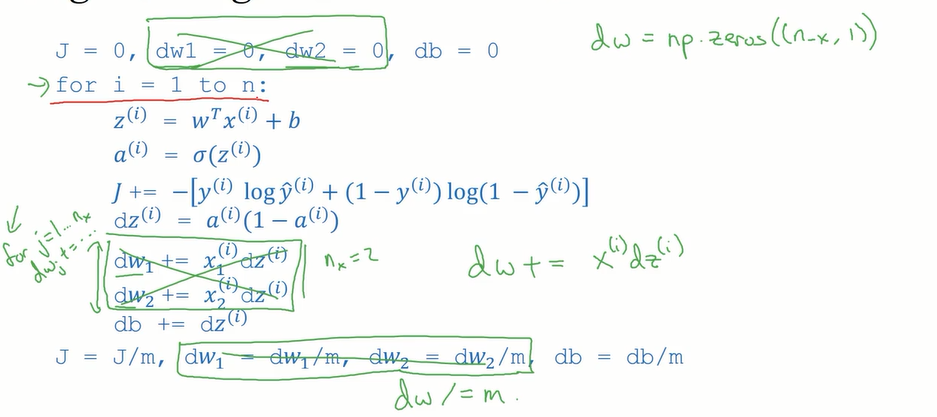
向量化logistic回归：（正向传播一步迭代的向量化实现，同时处理所有m个训练样本）

X矩阵由x进行竖排堆叠得到

Z矩阵由z进行横排堆叠得到

A矩阵由a进行横排堆叠得到

实现不需要for循环就可以从m个训练样本一次性计算出z和a

 

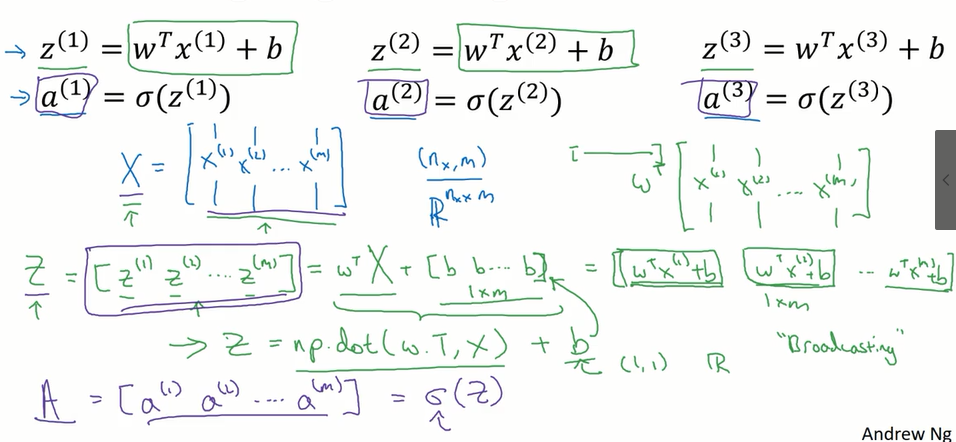
其中的Z=np.dot(w.T,X)+b ,在此b为一个实数，向量+实数，通过python的广播，可以将其扩展为1*m的行向量

 去掉反向传播中的所有for循环：

过程：

 

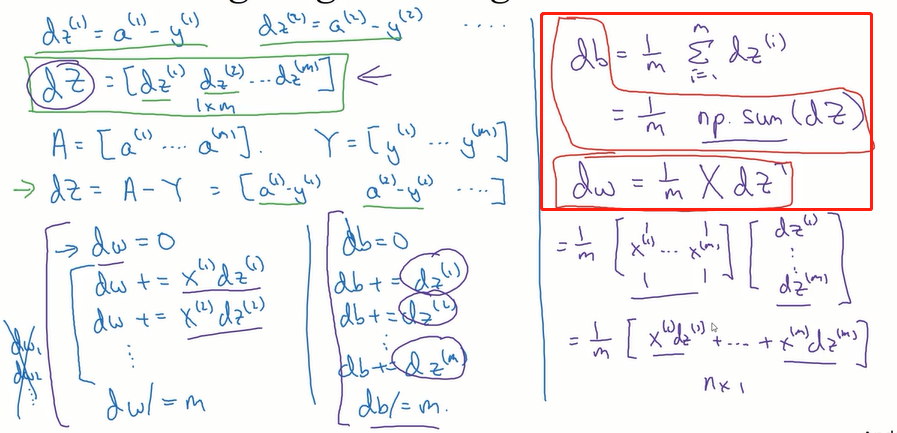
目前实现了对所有训练样本进行预测和求导：（没有使用for循环）

 

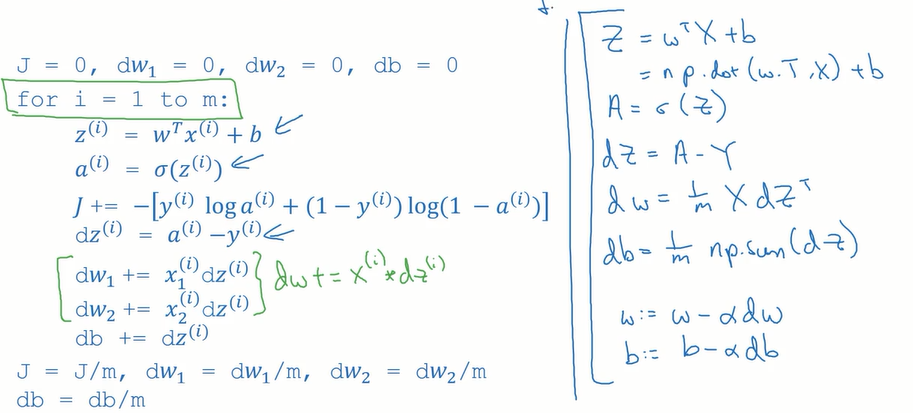
最外层循环有时候是无法去掉的（比如要求上千次导数进行梯度下降的情况）