逆变换采样和拒绝采样
蒙特卡罗方法（Monte Carlo）尝试利用计算机模拟（伪）随机数解决一类问题，这类问题通常具有以下特征：
- 所求解的问题本身具有 内在随机性，例如中子与原子核的相互作用受量子力学规律的制约；
- 所求解问题可以转化为某种随机分布的特征数，例如通过撒豆子的方式计算不规则图形的面积。蒙特卡洛法是一种以 概率统计理论 为指导的 数值计算 方法。
抽样（采样） 指从总体中抽取一部分作为样本。计算机模拟中，抽样意味着从一个概率分布中生成一个观察值，这涉及到一个随机的过程。一般认为计算机只能进行均匀分布的采样，对于复杂的概率分布，需要设计采样方法。
逆变换采样
从图像上可以十分形象地理解连续型随机变量的采样：
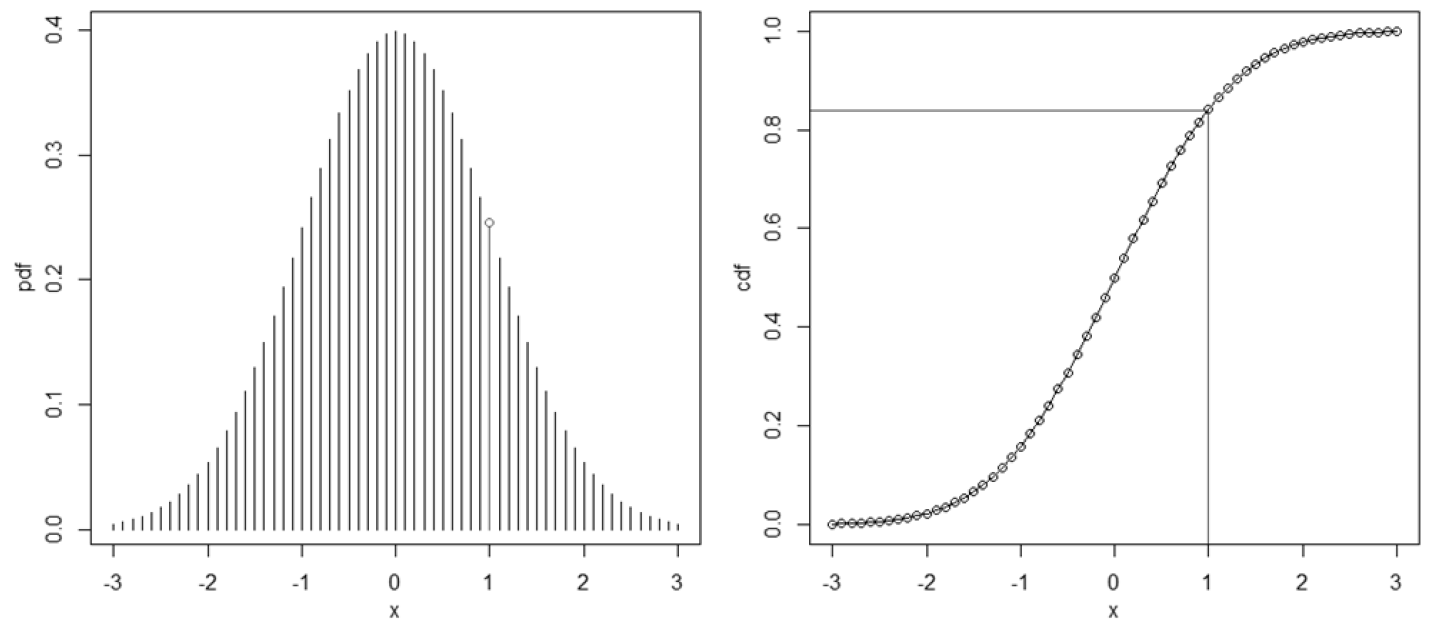
左图是正态分布的 概率密度函数（Probability Density Function，PDF）记为 \(f(x)\)，右图是正态分布的 累积分布函数（Cumulative Distribute Function，CDF）记为 \(F(x)\)。随机变量的采样就是在 \([0,1]\) 区间均匀分布采样的基础上，选取尽可能分散的点，使这些点尽可能地拟合累积分布函数的曲线。
拒绝采样
逆变换采样虽然简单有效，但是当累积分布函数或者反函数难求时却难以实施，而实际往往就是这样的。
下图中的 \(f(x)\) 是我们采样的目标 PDF，当其 CDF 或者 CDF 的反函数不容易求的时就不能直接对 \(f(x)\) 进行采样。拒绝采样（Rejection Sampling）的基本思想是借助这样一个参考概率密度函数 \(f_r(x)\) 即下图中的 \(\mathrm{Mg}(x)=\mathrm{M}\)：
- \(f_r(x)\) 十分容易进行采样，例如取均匀分布意味着参考 PDF 可以直接进行逆变换采样
- \(f_r(x)\) 位于 \(f(x)\) 上方，即对任意 \(x\) 有 \(f_r(x){\ge}f(x)\)
- \(\mathrm{Mg}(x)\) 表示将均匀分布 \(g(x)\) 向上移动，此时以 \(f(x)\) 的极大值确定 \(\mathrm{M}\) 的值效果比较好
从图上来看，参考 PDF “罩住”了目标 PDF：
拒绝采样的过程如下：
-
从 \(f_r(x)\) 进行一次采样 \(x_i\)
-
计算 \(x_i\) 的 接受概率 \(\alpha\)（Acceptance Probability）：
\[\alpha=\frac{f\left(x_{i}\right)}{f_r\left(x_{i}\right)} \] -
从 \((0,1)\) 均匀分布中进行一次采样 \(u\)
-
如果 \(\alpha{\ge}u\)，接受 \(x_i\) 作为一个来自 \(f(x)\) 的采样；否则，重复第1步
显然对于特定的目标 PDF，参考 PDF 不止一个，不同 PDF 的 \(\max(\alpha)\) 不同。以均匀分布采样为例，当参考 PDF 从上面越靠近目标 PDF 采样效率越高，相应的寻找这样的参考 PDF 的难度就越大。采样效率高意味着++对于那些概率密度较小的区域有更大的几率能够采样到++。
为了平衡采样效率和参考 PDF 的确定难度，提出了 自适应拒绝采样。
自适应拒绝采样
当参考 PDF 不能很好的“罩住”目标 PDF 时，那些未罩住区域内的采样点被拒绝的概率就会很大，采样效率低。所以如果能够找到一个跟目标 PDF 非常接近的参考 PDF，即参考 PDF 计划能够完全从上面贴合目标 PDF，此时能够达到较好的采样效率。
当目标 PDF 是 log-concave函数 时可以采用 自适应拒绝采样（Adaptive Rejection Sampling，ARS）。
log-concave函数：当概率密度函数 \(f(x)\) 是凹函数（concave）且 \(\log{f(x)}\) 仍然是凹函数时，\(f(x)\) 称之为 log-concave 函数：
\[f(\theta x+(1-\theta) y) \geq \theta f(x)+(1-\theta) f(y) \]
在 log-concave 函数上随机选取一些点做切线：
将log-concave函数变换回原来的PDF，此时上图的切线将变成曲线（取指数），它！们！弯！了！
将这组弯了的“切线”组成一个分段函数，这个分段函数将会很好的贴合目标 PDF。
