BZOJ 1502:月下柠檬树
BZOJ 1502:月下柠檬树
题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id=1502
题目大意:给出一棵由圆台构成的树以及一个平行光源,问树的阴影面积.
扫描线+自适应Simpson积分
首先给出$Simpson$公式:$\int_l^rf(x)dx \approx \frac{r-l}{6}[f(l)+4f(\frac{r-l}{2})+f(r)]$
上述公式只能得出一个近似值,通常情况下与真实值相差甚远,故需要稍加改进为自适应$Simpson$积分:
- 设$mid=\frac{r+l}{2}$,分别计算$L=Simpson(\int_l^{mid}f(x)dx)$,$R=Simpson(\int_{mid}^rf(x)dx)$,$S=Simpson(\int_l^rf(x)dx)$.
- 若$L+R=S$,则可以认为$S=\int_l^rf(x)dx$;否则用$Simpson$公式递归计算函数在$[l,mid]$和$[mid,r]$的积分.
对于某些不易计算函数积分,能自动调整精度,但误差较大(精度在题目所要求的基础上多加几位),适用于较平滑的曲线;需要注意的是,自适应$Simpson$积分很容易被数据卡掉(毕竟我们只通过$5$个点来大致确定一个图像的面积),故求面积时最好分段。
由于题中给出的为平行光,故圆台底面投影在地面上的图形仍为圆。我们将整颗树切分成无数个截面,故树的投影即为无数个圆的投影的面积交,投影图像大致如下:
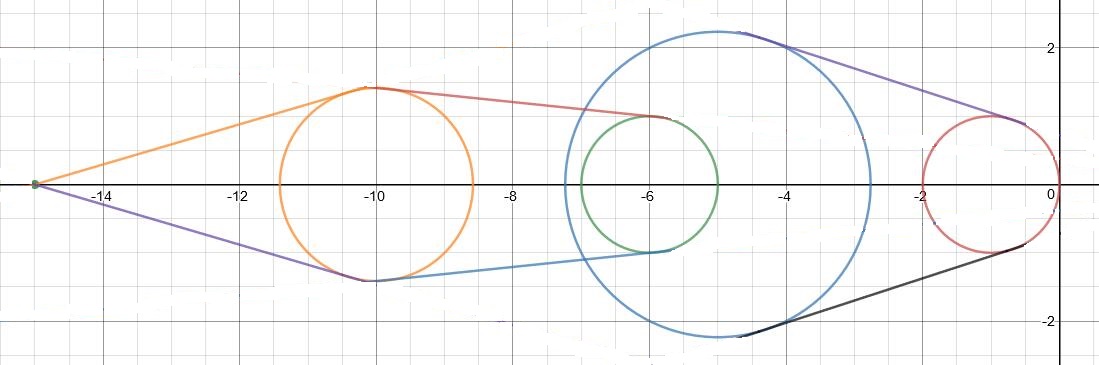
也就是说,阴影面积即为各个底面以及顶点的投影和两两圆的公切线所围成的面积。
设函数$F(t)$为扫描线$x=t$与上述图形所截的线段长度(显然$F(t)$是连续的),则阴影面积为$\int_L^RF(t)dt$,而这个积分可由$Simpson$公式轻松求得.
需要注意的是,若相邻两圆内含,则他们没有公切线。
代码如下:
1 #include <cstdio> 2 #include <iostream> 3 #include <cmath> 4 #define Min(a,b) (a<b?a:b) 5 #define Max(a,b) (a>b?a:b) 6 #define N 505 7 #define eps 1e-5 8 using namespace std; 9 const double inf=1e12; 10 int n,k; 11 double alpha,h0,h; 12 int dcmp(double x){ 13 if(fabs(x)<eps)return 0; 14 else return x<0?-1:1; 15 } 16 struct point{ 17 double x,y; 18 point(double X=0,double Y=0){x=X;y=Y;} 19 }; 20 struct circle{ 21 point p; 22 double r; 23 circle(point P=point(0,0),double R=0){p=P;r=R;} 24 bool within(circle t){ 25 return dcmp(fabs(p.x-t.p.x)-fabs(r-t.r))<=0; 26 } 27 }c[N]; 28 struct line{ 29 point p,q; 30 double k,b; 31 line(point P=point(0,0),point Q=point(0,0)){ 32 p=P;q=Q; 33 if(p.x>q.x)swap(p,q); 34 k=(p.y-q.y)/(p.x-q.x); 35 b=p.y-k*p.x; 36 } 37 double f(double x){ 38 return k*x+b; 39 } 40 }l[N]; 41 double F(double x){ 42 double len=0; 43 for(int i=0;i<n;++i){//枚举圆与扫描线所截的最大长度 44 double d=fabs(c[i].p.x-x); 45 if(d-c[i].r<0)len=Max(len,2*sqrt(c[i].r*c[i].r-d*d)); 46 } 47 for(int i=0;i<k;++i)//枚举公切线与扫描线所截的最大长度 48 if(l[i].p.x<x&&x<l[i].q.x)len=Max(len,fabs(l[i].f(x))*2); 49 return len; 50 } 51 double cal(double l,double r){ 52 double mid=(l+r)/2; 53 return (F(l)+4*F(mid)+F(r))*(r-l)/6; 54 } 55 double simpson(double l,double r,double s){ 56 double mid=(l+r)/2; 57 double x=cal(l,mid),y=cal(mid,r); 58 if(!dcmp(x+y-s))return s; 59 else return simpson(l,mid,x)+simpson(mid,r,y); 60 } 61 void solve(){ 62 double L=inf,R=-inf; 63 for(int i=0;i<=n;++i){ 64 L=Min(L,c[i].p.x-c[i].r); 65 R=Max(R,c[i].p.x+c[i].r); 66 } 67 for(int i=1;i<=n;++i){ 68 if(c[i].within(c[i-1]))continue;//两圆内含的情况 69 double sin_theta=(c[i].r-c[i-1].r)/(c[i].p.x-c[i-1].p.x); 70 double cos_theta=sqrt(1-sin_theta*sin_theta); 71 l[k++]=line(point(c[i].p.x-c[i].r*sin_theta,c[i].r*cos_theta), 72 point(c[i-1].p.x-c[i-1].r*sin_theta,c[i-1].r*cos_theta)); 73 } 74 printf("%.2lf\n",simpson(L,R,cal(L,R))); 75 } 76 int main(void){ 77 scanf("%d%lf%lf",&n,&alpha,&h0); 78 for(int i=0;i<n;++i){ 79 c[i].p=point(h0/tan(alpha),0); 80 scanf("%lf",&h); 81 h0+=h; 82 } 83 c[n].p=point(h0/tan(alpha),0);c[n].r=0; 84 for(int i=0;i<n;++i)scanf("%lf",&c[i].r); 85 solve(); 86 }
去掉部分判断语句后,从原来的TLE(6000ms)变成了372ms,不是很懂为什么差距这么大。



