数论习题（二）
（二）.筛子
- P4213 【模板】杜教筛
给定 \(1\le n< 2^{31}\)，求下面两个东西：
显然这个东西不能直接 \(O(n)\) 求，那么我们就用杜教筛！
1.筛 \(\varphi\)
我们知道 \(\varphi * 1=id\)，于是我们取 \(g=1\)，有：
也就是：
就OK了，直接筛就行。
2.筛 \(\mu\)
我们知道 \(\mu * 1=\varepsilon\)，于是我们取 \(g=1\)，有：
也就是：
就OK了，直接筛就行。
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const int N=1e6+7e5+10;
ll T=1;
ll n;
ll prime[N],v[N],mu[N],phi[N],tot;
ll smu[N],sphi[N];
map <ll,ll> mp_mu,mp_phi;
void shai(ll n){
phi[1]=1,mu[1]=1,v[1]=1;
for(int i=2;i<=n;i++){
if(!v[i]){
v[i]=i;prime[++tot]=i;mu[i]=-1;phi[i]=i-1;
}
for(int j=1;j<=tot;j++){
if(prime[j]>v[i] || prime[j]>n/i) break;
v[i*prime[j]] = prime[j];
if(i%prime[j]==0) mu[i*prime[j]]=0,phi[i*prime[j]]=phi[i] * prime[j];
else mu[i*prime[j]] = -mu[i],phi[i*prime[j]] = phi[i] * (prime[j]-1);
}
}
for(int i=1;i<=n;i++){
smu[i]=smu[i-1] + mu[i],sphi[i]=sphi[i-1]+phi[i];
}
}
ll sum_mu(ll n){
if(n<=N-10) return smu[n];
if(mp_mu.find(n)!=mp_mu.end()) return mp_mu[n];
ll res=1;
for(ll l=2,r;l<=n;l=r+1){
r= n/(n/l);
res-=(r-l+1) * sum_mu(n/l);
}return mp_mu[n]=res;
}
ll sum_phi(ll n){
if(n<=N-10) return sphi[n];
if(mp_phi.find(n)!=mp_phi.end()) return mp_phi[n];
ll res=n*(n+1)/2;
for(ll l=2,r;l<=n;l=r+1){
r= n/(n/l);
res-=(r-l+1) * sum_phi(n/l);
}return mp_phi[n]=res;
}
int main(){
shai(N-10);
scanf("%lld",&T);
for(int Case=1;Case<=T;Case++){
scanf("%lld",&n);
printf("%lld %lld\n",sum_phi(n),sum_mu(n));
}
return 0;
}
-BZOJ4176. Lucas的数论
给定 \(1\le n \le 10^9\)，求：
这玩意看着和 P3327 [SDOI2015] 约数个数和 很像，故我们直接照搬结论：
莫反拆开：
枚举 \(d\)：
然后两层都数论分块，\(\mu\) 的前缀和用杜教筛筛除来就行了。
复杂度不会推，但时限 3s，能过。
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const int N=5e6+10,mod=1000000007;
ll n;
ll prime[N],tot,v[N],mu[N];
map <ll,ll> mp;
void shai(ll n){
mu[1]=1;
for(int i=2;i<=n;i++){
if(v[i]==0){
v[i]=i,prime[++tot]=i;mu[i]=-1;
}
for(int j=1;j<=tot;j++){
if(prime[j] > v[i] || prime[j] > n/i) break;
v[i*prime[j]] = prime[j];
if(i%prime[j]==0) mu[i*prime[j]]=0;
else mu[i*prime[j]] = -mu[i];
}
}
for(int i=1;i<=n;i++) (mu[i] += mu[i-1])%=mod;
}
ll sum_mu(ll n){
if(n<=N-10) return mu[n];
if(mp.find(n)!=mp.end()) return mp[n];
ll res=1;
for(ll l=2,r;l<=n;l=r+1){
r= n/(n/l);
res-=(r-l+1) * sum_mu(n/l);
}return mp[n]=res;
}
int main(){
shai(N-10);
scanf("%lld",&n);
ll ans=0;
for(int l=1,r;l<=n;l=r+1){
r=n/(n/l);
ll cnt=0,m=n/l;
for(int lj=1,rj;lj<=m;lj=rj+1){
rj=m/(m/lj);
(cnt+=(rj-lj+1) * (m/lj) %mod) %=mod;
}
(ans += cnt*cnt%mod*(sum_mu(r)-sum_mu(l-1))%mod)%=mod;
}
printf("%lld\n",(ans+mod)%mod);
return 0;
}
-BZOJ3512. DZY Loves Math IV
给定 \(1\le n \le 10^5\)，\(1\le m\le 10^9\)，求：
首先我们知道：
很可惜，这个题没法用这个东西推（我试了，会推出来一个很长且没法算的东西），我们要用这个：
若 \(p\in\mathbb{P}\)，则：
我们重新看这个式子，发现 \(n\) 这一维很小，所以可以考虑先枚举 \(i\in[1,n]\)，分别求和。
我们记：
我们随便找一个 \(p\in\mathbb{P}\) 且 \(p\mid a\)，尝试把 \(a\) 拆成 \(\dfrac{a}{p}\times a\)，分情况讨论：
1.$ p^2 \nmid a$
此时我们无法保证是否存在 \(p^2\nmid ai\)，即有一部分 \(p\mid i\) 的情况下，有 \(p^2\mid ai\)。
于是原式变为：
带一下上面的式子，也就是：
我们可以把后半段的 \(p-1\) 强行 -1，然后再加上：
也就是：
依据 \(f\) 的定义，也就是：
2.$ p^2 \mid a$
我们此时能保证 \(p^2\mid ai\)，于是可以直接套公式：
也就是：
于是我们把 \(f\) 写成记忆化搜索，一直搜就行了
边界条件：
1.\(a=1\)
此时原式就是 \(\sum\limits_{i=1}^{n}\varphi(i)\)，跑杜教筛即可；
而这个 $m 又是之前的 \(m\) 除以一个数下取整得来的，和杜教筛内部的数论分块分界点相同，所以杜教筛只会跑一遍。
2.\(n=0\)
这时候直接返回 \(0\) 就行了，我因为没加这个而 MLE 了好久。
我们这个题要求的是：\(\sum\limits_{i=1}^{n}f(i,m)\)，枚举就行了。
至于为什么复杂度是对的，我也不会证awa
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef int ll;
const int N=1e6+10,mod=1e9+7,inv2=500000004;
ll n,m;
ll tot,v[N],phi[N],maxp[100010];
unordered_map <ll,ll> mpphi,mpf[100010];
vector <ll> prime;
void shai(ll n){
phi[1]=1,v[1]=1;
for(ll i=2;i<=n;i++){
if(!v[i]){
v[i]=i,prime.push_back(i);tot++;
phi[i]=i-1;
}
for(ll j=0;j<tot;j++){
if(prime[j] > v[i] || prime[j] > n/i) break;
v[i*prime[j]] = prime[j];
if(i%prime[j]==0) phi[i*prime[j]]=prime[j]*phi[i];
else phi[i*prime[j]]=(prime[j]-1)*phi[i];
}
}
for(int i=1;i<=100000;i++) maxp[i]=i;
for(ll i=1;i<=n;i++) (phi[i]+=phi[i-1])%=mod;
for(ll i=0;i<tot;i++){
for(ll j=prime[i];j<=100000;j+=prime[i]){
while(maxp[j] % prime[i]==0 && maxp[j]!=prime[i]) maxp[j]/=prime[i];
}
}
}
ll S_phi(ll n){
if(n<=N-10) return phi[n];
if(mpphi.find(n)!=mpphi.end()) return mpphi[n];
ll res=1ll*n*(n+1)%mod*inv2%mod;
for(ll l=2,r;l<=n;l=r+1){
r=n/(n/l);
(res-=1ll*(r-l+1)*S_phi(n/l)%mod)%=mod;
}
return mpphi[n]=(res+mod)%mod;
}
ll f(ll a,ll m){
if(mpf[a].find(m)!=mpf[a].end()) return mpf[a][m];
if(!m) return 0;
if(a==1){
return S_phi(m);
}
ll p=maxp[a],pa=a/p;
if(pa % p){
mpf[a][m]=(1ll*(p-1) * f(pa,m) %mod + f(a,m/p) ) %mod;
}else{
mpf[a][m]=(1ll*p * f(pa,m)) % mod;
}
return mpf[a][m];
}
int main(){
shai(N-10);
scanf("%d%d",&n,&m);
ll ans=0;
for(ll i=1;i<=n;i++){
(ans+=f(i,m))%=mod;
}
printf("%d\n",(ans+mod)%mod);
return 0;
}
-P3768 简单的数学题
给定 \(n\)，求：
直接上套路推式子，枚举 \(\gcd\)：
莫反拆开，\(d^2\) 提出去：
枚举 \(k\)：
\(i,j\) 上界有 \(dk\)，于是老套路令 \(T=dk\)，枚举 \(T\)：
后面那个关于 \(d\) 的式子，把 \(T^2\) 提出来，就是：
其中有 \(id*\mu\)，卷出来就是 \(\varphi\)
所以原式：
典中典数论分块，我们只需要尝试求出 \(f(T)=T^2\varphi(T)\) 的前缀和就行了，杜教筛嘛。
我们令 \(g=id^2\)，则：
也就是 \(f*g=id^3\)，即 \(id^2*f=id^3\)。
直接跑杜教筛就行了。
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const int N=1e7+10;
ll inv2,inv6,mod,n;
ll prime[N],tot,v[N],phi[N];
ll sf[N];
map <ll,ll> mp;
void shai(ll n){
phi[1]=1;v[1]=1;
for(ll i=2;i<=n;i++){
if(!v[i]){
v[i]=i,prime[++tot]=i;
phi[i]=i-1;
}for(ll j=1;j<=tot;j++){
if(prime[j]>v[i]||prime[j]>n/i) break;
v[i*prime[j]]=prime[j];
if(i%prime[j]==0) phi[i*prime[j]]=prime[j] *phi[i];
else phi[i*prime[j]]=(prime[j]-1)*phi[i];
}
}
for(ll i=1;i<=n;i++) sf[i]=(sf[i-1] + i%mod*i%mod*phi[i]%mod)%mod;
}
ll qpow(ll a,ll n){
ll res=1;
while(n){
if(n&1) res=(res*a)%mod;
a=(a*a)%mod,n>>=1;
}return res;
}
ll S_2(ll n){
n%=mod;
return n*(n+1)%mod*(2*n+1)%mod*inv6%mod;
}
ll S(ll n){
if(n<=N-10) return sf[n];
if(mp.find(n)!=mp.end())return mp[n];
ll res=n%mod*((n+1)%mod)%mod*inv2%mod;
res=(res*res)%mod;
for(ll l=2,r;l<=n;l=r+1){
r=n/(n/l);
(res-=(S_2(r)-S_2(l-1))%mod*S(n/l)%mod)%=mod;
}
return mp[n]=(res+mod)%mod;
}
int main(){
scanf("%lld%lld",&mod,&n);
inv2=qpow(2,mod-2)%mod;
inv6=qpow(6,mod-2)%mod;
shai(N-10);
ll ans=0;
for(ll l=1,r;l<=n;l=r+1){
ll nl=n/l;r=n/(n/l);
ll tmp=nl%mod*((nl+1)%mod)%mod*inv2%mod,ttt=(S(r)-S(l-1))%mod;
tmp=(tmp*tmp)%mod,ttt=(ttt+mod)%mod;
(ans+=tmp* ttt %mod)%=mod;
}printf("%lld\n",(ans%mod+mod)%mod);
return 0;
}
- P5325 【模板】Min_25 筛
min_25 筛即可。
我们令 \(f'_1(x)=x,f'_2(x)=x^2\)，对俩函数筛一遍，算就行了。
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const int N=2e5+10,mod=1e9+7;
const int inv2=500000004,inv6=166666668;
ll n,qn;
ll p[N],tot,v[N];
ll s1[N],s2[N];//质数前缀和&质数平方前缀和
ll m,id1[N],id2[N],w[N];//离散化
ll g1[N],g2[N];
void shai(ll n){
for(int i=2;i<=n;i++){
if(!v[i]){
v[i]=i,p[++tot]=i;
}for(int j=1;j<=tot;j++){
if(p[j] > v[i] || p[j] > n/i) break;
v[i*p[j]]=p[j];
}
}
for(int i=1;i<=tot;i++){
// (s1[i] += p[i]) %=mod;
// (s2[i] += p[i] * p[i] % mod) %=mod;
s1[i] = (s1[i-1] + p[i]) %mod;
s2[i] = (s2[i-1] + p[i] * p[i] % mod) %mod;
}return;
}
ll id(ll x){
if(x <= qn) return id1[x];
else return id2[n/x];
}
ll S(ll n,ll j){
if(p[j] > n) return 0;
ll res = (g2[id(n)] - g1[id(n)])%mod - (s2[j] - s1[j])%mod;
res=(res%mod+mod)%mod;
for(int k=j+1;k<=tot && p[k] * p[k] <= n;k++){
for(ll e=1,now=p[k];now<=n;now*=p[k],e++){
(res += now%mod * (now%mod-1) %mod * (S(n/now,k) + (e>1)) %mod)%=mod;
}
}return res;
}
int main(){
scanf("%lld",&n);qn=sqrt(n);shai(qn);
for(ll l=1,r;l<=n;l=r+1){
r=n/(n/l),w[++m]=n/l;
// printf("l:%lld r:%lld\n",l,r);
g1[m] = w[m]%mod * (w[m]%mod + 1) %mod * inv2 %mod -1;
g2[m] = w[m]%mod * (w[m]%mod + 1) %mod * (2 * w[m]%mod + 1) %mod *inv6 %mod -1;
if(w[m] <= qn) id1[w[m]]=m;
else id2[n/w[m]] = m;
}//离散化
//这里通过滚动数组优化。
for(ll j=1;j<=tot;j++){//j是阶段，我们先枚举j，当然直接枚到tot就行，因为筛的质数最大到根号n
for(ll i=1;i<=m && p[j] * p[j] <= w[i];i++){
//根据转移术式，当pj*pj>wi时，根本就不用变！
(g1[i] -= p[j] * (g1[id(w[i]/p[j])] - s1[j-1] )%mod )%=mod;
(g2[i] -= p[j] * p[j] % mod * (g2[id(w[i]/p[j])] - s2[j-1] )%mod )%=mod;
(g1[i] += mod )%=mod;(g2[i] += mod) %=mod;
}
}
ll ans=S(n,0) + 1;
printf("%lld\n",(ans+mod)%mod);
return 0;
}
//10000000000
- loj6053. 简单的函数
给定积性函数 \(f\)，满足：
给定 $1\le n\le $，求 \(\sum\limits_{i=1}^{n}f(i)\)。
我们使用 min_25 筛。
对于质数 \(p\)，显然有：
可以先忽略 \([p=2]2\) 部分，对 \(f'_1(p)=1\) 和 \(f'_2(p)=p\) 的 \(g\) 筛出来，然后拟合 \(v\) 函数，做就行了。
（函数名参见此博客）
我们发现，\(f(2)\) 处的值我们少算了 \(2\)，于是在最后把答案额外加二就行了。
但我突然好奇为什么？
比如一个例子：令 \(n=2\)。
因为假如说 \(f(2)=1,f(3)=2\)，那么就会算出错误的 \(f(6)=1\times 2=2\)，这显然是错误的，即为什么 \(f(2)\) 少算的值不会影响其它的计算？
我们把 \(S\) 函数的递推式和求解 \(S\) 的函数代码搬过来：
ll S(ll n,ll j){
if(p[j] > n) return 0;
ll res = (g2[id(n)] - g1[id(n)])%mod - (s2[j] - s1[j])%mod;
res=(res%mod+mod)%mod;
for(int k=j+1;k<=tot && p[k] * p[k] <= n;k++){
for(ll e=1,now=p[k];now<=n;now*=p[k],e++){
(res += (p[k] ^ e) %mod * (S(n/now,k) + (e>1)) %mod)%=mod;
}
}
return res;
}
我们有 \(q(n)=\sum\limits_{i=1}^{n}f(i)[i\in\mathbb{P}]\)。
注意到，我们只在第一次调用 \(S(n,0)\) 时，\(\sum\limits_{i=1}^{j}f(P_i)\) 中不包含错误的 \(f(2)\)，而 \(q(n)\) 中始终包含 \(f(2)\)。
这意味着，在我们调用 \(S(n,j)\)，其中 \(j>0\) 时，\(q\) 与 \(\sum\limits_{i=1}^{j}f(P_i)\) 中的 \(f(2)\) 会抵消掉，且后面的循环从 \(k=j+1\) 开始枚举，不会产生额外的影响。
在 \(j=0\) 时，我们 \(k\) 会从 \(1\) 开始枚举，而 \(e\) 也会从 \(1\) 开始枚举，注意到代码里写的是 p[k]^e，即 \(P_k\operatorname{xor}1\)，即 \(2\operatorname{xor}1\)，并没有任何错误的 \(f(2)\) 带来影响！！！
唯一出现影响的 \(f(2)\)，只在计算 (g2[id(n)] - g1[id(n)]) 中出现了一次！
所以我们最后只需要加上 \(2\) 就能得到正确的答案了。
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const int N=2e5+10,mod=1e9+7;
const int inv2=500000004,inv6=166666668;
ll n,qn;
ll p[N],tot,v[N];
ll s1[N],s2[N];//质数前缀和&质数平方前缀和
ll m,id1[N],id2[N],w[N];//离散化
ll g1[N],g2[N];
void shai(ll n){
for(int i=2;i<=n;i++){
if(!v[i]){
v[i]=i,p[++tot]=i;
}for(int j=1;j<=tot;j++){
if(p[j] > v[i] || p[j] > n/i) break;
v[i*p[j]]=p[j];
}
}
for(int i=1;i<=tot;i++){
s1[i] = (i)%mod;
s2[i] = (s2[i-1] + p[i] % mod) %mod;
}return;
}
ll id(ll x){
if(x <= qn) return id1[x];
else return id2[n/x];
}
ll S(ll n,ll j){
if(p[j] > n) return 0;
ll res = (g2[id(n)] - g1[id(n)])%mod - (s2[j] - s1[j])%mod;
res=(res%mod+mod)%mod;
for(int k=j+1;k<=tot && p[k] * p[k] <= n;k++){
for(ll e=1,now=p[k];now<=n;now*=p[k],e++){
(res += (p[k] ^ e) %mod * (S(n/now,k) + (e>1)) %mod)%=mod;
}
}
return res;
}
ll f1(ll x){
return (x-1) %mod ;
}
ll f2(ll x){
x%=mod;
return x * (x+1) %mod *inv2 %mod -1;
}
int main(){
scanf("%lld",&n);qn=sqrt(n);shai(qn);
for(ll l=1,r;l<=n;l=r+1){
r=n/(n/l),w[++m]=n/l;
g1[m] = f1(w[m]);
g2[m] = f2(w[m]);
if(w[m] <= qn) id1[w[m]]=m;
else id2[n/w[m]] = m;
}//离散化
for(ll j=1;j<=tot;j++){//j是阶段，我们先枚举j，当然直接枚到tot就行，因为筛的质数最大到根号n
for(ll i=1;i<=m && p[j] * p[j] <= w[i];i++){
(g1[i] -= ( 1) %mod * (g1[id(w[i]/p[j])] - s1[j-1] )%mod )%=mod;
(g2[i] -= p[j] %mod * (g2[id(w[i]/p[j])] - s2[j-1] )%mod )%=mod;
(g1[i] += mod )%=mod;(g2[i] += mod) %=mod;
}
}
ll ans=S(n,0) + 1 ;
if(n>=2) ans+=2;
printf("%lld\n",(ans+mod)%mod);
return 0;
}
- 51nod 1847 奇怪的数学题
我们记 \(\operatorname{sgcd}(n,m)\) 为 \(n,m\) 的次大公约数。
给定 \(1\le n\le 10^9,1\le \alpha\le 50\)，求：
对 \(2^{32}\) 取模的值。
（为了防止变量名重复，我们把原题中的 \(k\) 均替换为 \(\alpha\)）
这个题融合了杜教筛，min_25筛，莫反推式子，甚至从未听说过的第二类斯特林数求自然数幂和！
为了方便表示，我们令 \(\operatorname{lcp}(a)=\min\limits_{p|a}p\)
显然，我们有：
于是我们推式子，枚举 \(\gcd\)：
如果 \(i\) 和 \(j\) 的上界不同，我们只能莫反拆开，但由于这里两者上界相同，我们直接考虑利用 \(\varphi\) 的性质将其转化成 \(\varphi\)：
（注意这个“\(-1\)”在关于 \(i\) 的求和外面！）
于是我们对 \(d\) 进行数论分块，后者可以杜教筛筛 \(\varphi\)，我们重点考虑前者的前缀和怎么求。
我们设 \(f(n)=\left(\dfrac{n}{\operatorname{lpf}(n)}\right)^\alpha\)，求 \(\sum\limits_{i=1}^{n}f(i)\)。
我们讨论 \(n\) 为质数和合数，分别考虑：
\(n\) 为质数
此时显然有 \(f(n)=1\)，故我们索求的其实就是 \(n\) 以内的素数个数。
我们使用不完整的 min_25 筛：令 \(f'(p)=1\)，我们令 \(g\) 函数：
对这个函数求：
即 \(\sum\limits_{i=2}^{n}f'(i)[i\in\mathbb{P}]\) 即可，显然这两者时等价的。
当然，我们最终求出来的 \(g\) 数组，包含了 \(n\) 取遍 \(\lfloor\dfrac{n}{1}\rfloor,\lfloor\dfrac{n}{2}\rfloor\dots \lfloor\dfrac{n}{n}\rfloor\) 这些值，所有的 \(g\) 之值。这些数会在统计答案是有用。
（关于为什么把 \(g\) 的定义写出来，是害怕自己看不懂）
\(n\) 为合数
我们令 \(f'(n)=n^\alpha\)，对 \(f'\) 进行不完整的 min_25 筛。
我们把所有的合数按照其最小质因数进行分类。
然后我们关注 min_25 筛中 \(g\) 函数的递推过程，发现有：
当 \(P_j^2\le n\) 时，\(g(n,j-1)\) 比 \(g(n,j)\) 多出来的贡献为：
我们这里其实找到了一类合数，它们有共同特征：最小质因子为 \(P_j\)。
我们要求这一系列合数，它们的 \(\left(\dfrac{n}{\operatorname{lpf}(n)}\right)^\alpha\) 之和，即 \(f\) 之和（注意是 \(f\) 不是 \(f'\)！不要搞混！）。
其实我们发现上述贡献式中后面一部分，即 \(g(\frac{n}{P_j},j-1) - \sum\limits_{i=1}^{j-1}f'(P_i))\)，它的实际含义其实就是这些合数，除掉它们的最小质因子 \(P_k\) 后，剩余东西的 \(\alpha\) 次方和！也就是 \(f\) 之和！！！
故我们在求 \(g(n,0\sim \max\limits_{P_k^2\le n}k)\)，时，把所有的 \(g(\frac{n}{P_j},j-1) - \sum\limits_{i=1}^{j-1}f'(P_i))\)加到一个 \(h_n\) 里面，就能够得到对于 \(n\) 以内所有的合数，它们的 \(f\) 之和。
注意这里的 \(n\) 会取遍 \(\lfloor\dfrac{n}{1}\rfloor,\lfloor\dfrac{n}{2}\rfloor\dots \lfloor\dfrac{n}{n}\rfloor\) 这些值，所以我们也会得到一个 \(h\) 数组，存了 \(h_{\lfloor\frac{n}{1}\rfloor},h_{\lfloor\frac{n}{2}\rfloor}\dots h_{\lfloor\frac{n}{n}\rfloor}\) 这些值，这在我们最终统计答案时有用。
还有一个东西差点忘了说了，在我们求合数部分时，我们需要为 \(g\) 赋初始值，即：
显然不能枚举，我们需要拉插，但模数不支持逆元，所以我们只能用别的方式。
这里就用了一个神奇的东西：第二类斯特林数求自然数幂和。
即：
其中下降幂为 \(x^{\underline{n}}=x(x-1)(x-2)\dots(x-n+1)\)。
\(\begin{Bmatrix}k\\j\end{Bmatrix}\) 为第二类斯特林数，有个递推式：
\(\begin{Bmatrix}n\\m\end{Bmatrix}=\begin{Bmatrix}n-1\\m-1\end{Bmatrix} + m\begin{Bmatrix}n-1\\m\end{Bmatrix}\)
初始值：\(\begin{Bmatrix}0\\0\end{Bmatrix}=1\)
这个东西可以 \(O(\alpha^2)\) 预处理处斯特林数，每次 \(O(k^2)\) 查询自然数幂和，一共查询 \(\sqrt n\) 次，复杂度可以接受。
最后我们可以数论分块原式子，通过手玩，可以发现数论分块的右端点 \(r\) 组成的集合，与数论分块中 \(\lfloor\frac{n}{l}\rfloor\) 组成的集合相同！于是我们只需要进行一次上述过程，就能把前半部分所有取值的前缀和都求出来！
而后面的 \(\varphi\) 通过杜教筛算就行。
说一点后话：啊啊啊啊啊啊啊啊啊啊啊啊啊啊逆天啊啊啊啊啊啊啊啊啊啊啊
我调了好久，原因是：
for(int j=1;j<=tot;j++){
for(int i=1;i<=m &&1ll * prime[j] * prime[j] <= w[i];i++){
int idx=id(w[i]/prime[j]);
g1[i] -= (g1[idx] - s1[j-1] ) ;
h[i] += g2[idx] - s2[j-1];
g2[i] -= pk[j] * (g2[idx] - s2[j-1] ) ;
}
}
这一段代码，由于我筛出了 \(10^6\) 以内的所有质数，所以 prime[j] * prime[j] 必须要乘以 1ll ！！！！！不然就会炸掉，然后莫名进入这个内层循环跑一遍！！！！！！！！！！
太离谱了！！！！！！！！！！！！
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef unsigned int ll;
const int N=1e9+10,M=1e6+10,K=1e6+10,ALP=55;
ll n,alp;
ll prime[K],tot,v[K],phi[K];
ll s1[M],s2[M],pk[M];
ll qpow(ll a,ll n){
ll res=1;
while(n){
if(n&1) res *= a;
a*=a;n>>=1;
}return res;
}
void shai(ll n){
phi[1]=1;
for(ll i=2;i<=n;i++){
if(!v[i]){
v[i]=i,prime[++tot]=i;
phi[i]=i-1;
}for(ll j=1;j<=tot;j++){
if(prime[j] > v[i] || prime[j] > n/i) break;
v[i*prime[j]] = prime[j];
if(i%prime[j] == 0) phi[i*prime[j]] = phi[i] * prime[j];
else phi[i*prime[j]] = phi[i] * (prime[j]-1);
}
}
for(ll i=1;i<=n;i++) phi[i] += phi[i-1];
for(ll i=1;i<=tot;i++){
s1[i] = s1[i-1] + 1;
pk[i] = qpow(prime[i],alp);
s2[i] = s2[i-1] + pk[i];
}
}
ll stl[ALP][ALP];
ll zrsmh(ll n){
ll res=0;
if(n<=alp){
for(ll i=1;i<=n;i++){
ll tmp=1;
for(ll j=1;j<=alp;j++) tmp *= i;
res += tmp;
}return res;
}
for(ll j=0;j<=alp;j++){
ll tmp=1;
for(ll l=0;l<j+1;l++){
if((n+1-l) % (j+1) )tmp *= (n+1-l);
else tmp *= (n+1-l) / (j+1);
}res += tmp * stl[alp][j];
}return res;
}
ll m,qn,w[M],id1[M],id2[M],g1[M],g2[M],h[M];
ll f1(ll x){
return x-1;
}
ll f2(ll x){
return zrsmh(x) - 1;
}
int id(int x){
if(x <= qn) return id1[x];
else return id2[n/x];
}
ll tph[M];
bool vis[M];
ll Sphi(ll x){
if(x<=K-10) return phi[x];
if(vis[id(x)]) return tph[id(x)];
ll res=1ll * x*(x+1)/2;
vis[id(x)]=1;
for(ll l=2,r;l<=x;l=r+1){
r= x/(x/l);
res-=(r-l+1) * Sphi(x/l);
}return tph[id(x)]=res;
}
void Init(){
qn=sqrt(n);
stl[0][0]=1;
for(ll i=1;i<=alp;i++){
for(ll j=1;j<=alp;j++){
stl[i][j]=stl[i-1][j-1] + j * stl[i-1][j];
}
}
for(ll l=1,r;l<=n;l=r+1){
r=n/(n/l),w[++m]=n/l;
g1[m] = f1(w[m]);
g2[m] = f2(w[m]);
if(w[m] <= qn) id1[w[m]]=m;
else id2[n/w[m]] = m;
}
for(int j=1;j<=tot;j++){
for(int i=1;i<=m &&1ll * prime[j] * prime[j] <= w[i];i++){
int idx=id(w[i]/prime[j]);
g1[i] -= (g1[idx] - s1[j-1] ) ;
h[i] += g2[idx] - s2[j-1];
g2[i] -= pk[j] * (g2[idx] - s2[j-1] ) ;
}
}
}
ll ask(ll x){
return g1[id(x)] + h[id(x)] ;
}
int main(){
scanf("%u%u",&n,&alp);
shai(K-10);Init();
ll ans=0;
Sphi(n);
ll lst=0,now;
for(int l=1,r;l<=n;l=r+1){
r=n/(n/l);
now=ask(r);
ans += (2*Sphi(n/l)-1)*(now-lst);
lst=now;
}
cout<<ans<<endl;
return 0;
}
（三）.自然数幂和与拉格朗日插值
-BZOJ2137. submultiple
给定 \(\displaystyle m=\prod\limits_{i=1}^{n}p_i^{a_i}\)，求：
其中测试点 \(\textbf{A}\) 中 \(1\le a_i\le 10^5,1\le k \le 2^{31}-1\)，测试点 \(\textbf{B}\) 中 \(1\le a_i\le 2^{63}-1,1\le k\le 12\)
既然题目给好了 \(m\) 的质因数分解，我们可以按照每个质因数选多少个，来枚举 \(m\) 的因数。
而约数个数函数 \(d\) 刚好有一个和质因数次数相关的公式，于是原式：
也就是：
整个写成 \(\prod\) 记号：
这其实就是算 \(n\) 次自然数幂和，我们分别解决不同范围的测试点。
1.测试点 \(\textbf{A}\)
这个点中 \(a\) 小，\(k\) 大，直接预处理+前缀和就行了。
复杂度 \(O(k\log k\sum a )\)
2.测试点 \(\textbf{B}\)
这个点中 \(a\) 大，\(k\) 小，直接拉格朗日插值就行了。
复杂度 \(O(nk^2)\)
具体做法在这篇博客里。
这样这个题就做完了
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const int N=1e5+10,mod=1000000007;
ll n,k,a[N],maxn;
ll sum[N],inv[N];
ll qpow(ll a,ll n){
ll res=1;
while(n){
if(n&1) res=(res*a)%mod;
a=(a*a)%mod,n>>=1;
}return res;
}
void getS(ll n){
for(int i=1;i<=n;i++)sum[i]=(sum[i-1] + qpow(i,k))%mod;
}
void solve1(){
ll ans=1;getS(maxn+1);
for(int i=1;i<=n;i++){
(ans*=sum[a[i]+1])%=mod;
}printf("%lld\n",(ans+mod)%mod);
}
void solve2(){
getS(k+2);ll ans=1;
for(int i=-(k+2);i<=k+2;i++){
inv[i+k+2]=qpow((i+mod)%mod,mod-2);
}
for(int d=1;d<=n;d++){
ll cnt=0;
for(int i=1;i<=k+2;i++){
ll tot=1;
for(int j=1;j<=k+2;j++){
if(i==j) continue;
(tot*=(a[d]+1-j)%mod * inv[i-j+k+2] %mod)%=mod;
}
(cnt+=sum[i]*tot%mod)%=mod;
}
(ans*=cnt)%=mod;
}printf("%lld\n",(ans+mod)%mod);
}
int main(){
scanf("%lld%lld",&n,&k);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
maxn=max(maxn,a[i]);
}
if(k>12) solve1();
else solve2();
return 0;
}
-BZOJ3453. tyvj 1858 XLkxc
有如下函数：
现在给定 \(1\le k,a,n,d\le 123456789\)，求 \(h(n)\bmod 1234567891\)。
我们先把要求的这个东西直接拆开！
cy言：「积分多一次，求导少一次」
我们发现 \(j^k\) 是个 \(k\) 次的，而求和符号 \(\sum\) 可以看做特殊的积分符号 \(\int\)，
那么这个式子相当于在 \(k\) 次的式子上套了三个积分，那就多三次，所以这是个关于 \(n\) 的 \(k+3\) 次多项式。
于是我们只要知道这个式子在 \(n\in[1,k+4]\) 时的取值，就可以拉格朗日插值插出来这个式子。
我们考虑怎么求值。
第一层，枚举 \(n\in[1,k+4]\)，复杂度 \(O(k)\)；
第二层，枚举 \(u\in[0,n]\)，复杂度 \(O(k)\)；（严格来说外面两层一起算是 \(O(n\log n)\) 的）
第三层，枚举 \(i\in[1,a+ud]\)，发现太大了，没法枚举。但如果我们记这么一个函数：
，那么这一层我们要求的就是 \(t(a+ud)\)。
\(t\) 函数中 \(n\) 的取值是 \(10^{16}\)，很大，于是我们可以考虑再套一层拉格朗日插值，把 \(t\) 函数插出来。
根据「积分多一次，求导少一次」，我们发现，\(t\) 函数是个 \(k+2\) 次的多项式，需要求出 \(t(n),n\in[1,k+3]\) 这 \(k+3\) 个点值，才能插出来。
我们把此时的预处理放到最后说，我们假定现在可以插出来这个 \(t\) 了。
于是第三层循环的复杂度就是一个拉格朗日插值的复杂度，我给它做到了 \(O(k\log k)\)。
所以这么一段求原式在 \(n\in[1,k+4]\) 处的取值的处理，总复杂度是 \(O((k\log k)^2)\)，非常小，可以接受。（不确定有没有分析错，先放着吧，等人来 hack）
我们现在考虑一下 \(t(n),n\in[1,k+3]\) 的取值咋求。
预处理 \(i^n,n\in[1,k+3]\)，然后直接枚举就行了，\(O(k\log k)\)。
现在我们已经求出了 \(n\in[1,k+4]\)，原式的取值。
那么我们直接跑拉格朗日插值硬插就行了，嫌麻烦直接写 \(O(k^2)\) 的就行。
这样我们这个题就做完了，代码实现的细节蛮多，但好爽！
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const int N=1010,mod=1234567891,del=300;
ll T=1;
ll k,a,n,d;
ll aud[N],pd[N],nd[N];
ll inv[N];
ll qpow(ll a,ll n){
ll res=1ll;
while(n){
if(n&1ll) res=(res*a)%mod;
a=(a*a)%mod;n>>=1ll;
}return res;
}
void Init_inv(){
for(ll i=-230;i<=230;i++){
inv[i+del]=qpow((i+mod)%mod,mod-2);
}
}
void Init_aud(){//m=O(100)
for(ll i=1;i<=k+100;i++){
pd[i]=qpow(i,k)%mod;
}
for(ll n=1;n<=k+4;n++){
aud[n]=0;
for(ll i=1;i<=n;i++){
for(ll j=1;j<=i;j++){
(aud[n]+=pd[j]%mod)%=mod;
}
}
}
}
void Init_n(){
for(ll n=1;n<=k+4;n++){
nd[n]=0;
for(ll u=0;u<=n;u++){
ll now=(a+u*d%mod)%mod;
if(now<=k+3){
(nd[n]+=aud[now])%=mod;
continue;
}
ll M=1,Z=1,tot=0;
for(ll j=1;j<=k+3;j++) (M*=(now-j)%mod)%=mod;
for(ll j=-1;j>=-k-2;j--) (Z*=inv[j+del])%=mod;
for(ll i=1;i<=k+3;i++){
ll zi=M*qpow(((now-i)%mod+mod)%mod,mod-2) %mod;
ll tmp=(-k-4+i)%mod+mod;
if(i>1) (Z*=tmp%mod * inv[i-1+del]%mod)%=mod;
(tot+=aud[i]*zi%mod*Z%mod)%=mod;
}
(nd[n]+=tot)%=mod;
}
}
}
int main(){
Init_inv();
scanf("%lld",&T);
for(int Case=1;Case<=T;Case++){
scanf("%lld%lld%lld%lld",&k,&a,&n,&d);
Init_aud();
Init_n();
if(n<=k+4){
printf("%lld\n",(nd[n]+mod)%mod);
continue;
}
ll ans=0;
for(ll i=1;i<=k+4;i++){
ll tmp=1ll;
for(ll j=1;j<=k+4;j++){
if(i==j) continue;
(tmp*=(n-j)%mod*inv[i-j+del]%mod)%=mod;
}
(ans+=tmp%mod*nd[i]%mod)%=mod;
}printf("%lld\n",(ans+mod)%mod);
}
return 0;
}
- P6271 [湖北省队互测2014] 一个人的数论
给定：
求：
直接推式子：
枚举 \(d\)：
也就是：
给出了 \(N\) 的质因数分解，且 \(d\) 是 \(N\) 的因数，所以直接枚举 \(d\) 的质因数分解：
注意到只要存在 \(i_k>1\)，\(\mu\) 就是 \(0\)，所以只需要枚举每个 \(i_k=[0,1]\)：
借助 \(\color{red}\mathfrak{zzafanti}\) 之力，我们发现后面那一大坨是一个 \(Q+1\) 次的关于那坨上界的多项式，我们写成多项式形式：
于是乎，我们考虑枚举 \(j\)：
这几个函数都是积性函数，所以直接把里面的求积提出来：
这里头有一个 \(a_j\cdot \prod\limits_{k=1}^{w}p_k^{j\alpha_k}\) 是与 \(i\) 无关的，于是提到最前头：
里面的东西稍微合并一下：
我们记 \(f(k)=\mu(p_k^{i_k})\cdot p_k^{(Q-j)i_k}\)，则原式：
发现 \(f(1)\) 只与 \(i_1\) 有关，\(f(2)\) 只与 \(i_2\) 有关……于是这些都可以提出去，原式变成：
也就是：
我们观察 \(i_k\) 分别取 \(0\) 和 \(1\) 时，\(f(k)\) 为多少：
- \(i_k=0\)
- \(i_k=1\)
此时，原式就变成了：
用高斯消元或者拉格朗日插值把 \(a\) 插出来，复杂度用高斯消元的话是 \(O(Q^3)\)；
直接暴算这个式子，预处理 \(\prod\limits_{v=1}^{w}p_v^{\alpha_v}\)是 \(O(w\log \max(\alpha))\)，预处理出 \(p_k^{j}\;,\;k\in[1,w]\;,\;j\in[1,Q]\) 是 \(O(w\log Q)\)，而整个式子在预处理的情况下能跑到 \(O(wQ)\)
总复杂度就是 \(O(Q^3+wQ+w\log \max(\alpha)+w\log Q)\)，能过。
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const int N=1010,mod=1e9+7;
ll Q,w,p[N],alp[N],P[N][N];
ll x[N],y[N],a[N],f[N],g[N],h[N];
ll qpow(ll a,ll n){
if(n==-1) n=mod-2;
ll res=1;
while(n){
if(n&1) res=(res*a)%mod;
a=(a*a)%mod;n>>=1;
}return res;
}
void lagrange(ll n){//时刻记住：给出了 Q+2 个点值！
for(int i=0;i<n;i++) x[i]=i+1;
for(int i=0;i<n;i++) y[i]=(y[i-1]+qpow(i+1,Q))%mod;//求点值
// for(int i=0;i<n;i++){
// printf("i:%d x:%lld y:%lld\n",i,x[i],y[i]);
// }
for(int i=0;i<n;i++){
a[i]=1;
for(int j=0;j<n;j++){
if(i==j) continue;
(a[i] *= (x[i]-x[j])%mod )%=mod;
}a[i] = qpow(a[i],-1) * y[i]%mod;
}//求a
g[0]=1;//最初，是个0次的多项式 "1"
for(int i=0;i<n;i++){//给它乘上一个 (m-x[i])
for(int j=i+1;j>=1;j--){
g[j] = ( g[j-1] - g[j] * x[i]%mod ) %mod;
}g[0]= g[0] * (-x[i])%mod;
}//求g
for(int i=0;i<n;i++){
ll inv=qpow(-x[i],-1);
if(!inv){//x[i]=0
for(int j=0;j<n;j++) h[j]=g[j+1];
}else{
h[0]=g[0] * inv%mod;
for(int j=1;j<n;j++){
h[j] = (g[j] - h[j-1])%mod *inv%mod;
}
}
for(int j=0;j<n;j++){
(f[j] += a[i] * h[j]%mod) %=mod;
}
}
for(int i=0;i<n;i++) f[i]=(f[i]+mod)%mod;
}
ll calc(ll n){
ll res=0;
for(int i=Q+1;i>=0;i--) res= (res * n%mod + f[i])%mod;
return (res+mod)%mod;
}
int main(){
scanf("%lld%lld",&Q,&w);
for(int i=1;i<=w;i++){
scanf("%lld%lld",&p[i],&alp[i]);
}
lagrange(Q+2);
ll A=1,NOWA=1,ans=0;
for(int k=1;k<=w;k++){
for(int i=-1;i<=Q;i++){
P[k][i +1]=qpow(p[k],i);
}
}
for(int v=1;v<=w;v++) (A*=qpow(p[v],alp[v]))%=mod;
for(int j=0;j<=Q+1;j++){
if(j) (NOWA*=A)%=mod;
ll tmp=1;
for(int k=1;k<=w;k++){
(tmp*=(1-P[k][Q-j +1])%mod)%=mod;
}
(ans+=f[j] * NOWA%mod *tmp%mod)%=mod;
}printf("%lld\n",(ans+mod)%mod);
return 0;
}
这里附一张我在没求助 \(\color{red}\mathfrak{zzafanti}\) 之前盯着式子发呆画出的《一个「人」的数论》：
四.同余题目
- BZOJ2219. 数论之神
太困难了，于是看了题解。
给定正整数 \(A,B,K\)，求方程：
在 \([0,2K)\) 以内的解的个数。
首先我们将 \(2K+1\) 分解质因数为 \(\prod\limits_{i=1}^{k}p_i^{c_i}\)，我们索求的答案即为如下 \(k\) 个方程：
的乘积。
这个东西能用中国剩余定理得出（待会再写）。
于是我们着手于解决问题：
的解的个数（我们令 \(B<p^\alpha\)）。
分三种情况讨论：
1.\(B=0\)
即为求方程：
的解的数量。
这个方程的含义就是：\(x^A\) 为 \(p^\alpha\) 的倍数。我们先找到 \(x\) 为 \(p\) 的幂的最小整数解。
设 \(x=p^{k}\)，则有：
即：
此时 \(k\) 的最小整数解为 \(\lfloor \frac{\alpha-1}{A} \rfloor+1\)。
于是我们便有了 \(x\) 的最小整数解：
我们欲求解的个数，即为 \(x<p^\alpha\) 时 \(x_0\) 的倍数的个数，显然为 \(\dfrac{p^\alpha}{x_0}\) 个。
于是这种情况下，解的个数即为：
2.\(\gcd(B,p^\alpha)>1\)
我们令 \(B=b\cdot p^{cnt}\)，其中 \(b\) 与 \(p\) 互质，则有：
我们将同余式化为等式，即：
再令等式左右两边同时除以 \(p^{cnt}\)：
我们发现等式右边为 \(p\) 的倍数，而 \(b\) 不是 \(p\) 的倍数，则 \(\dfrac{x^A}{p^{cnt}}\) 也一定不为 \(p\) 的倍数。
故当 \(cnt\) 不为 \(A\) 的倍数，即 \(cnt\bmod A\ne0\) 时，\(\dfrac{x^A}{p^{cnt}}\) 一定是 \(p\) 的倍数，此时方程无解。
我们再把方程改写为同余式的形式：
由于 \(cnt\) 为 \(A\) 的倍数，于是可以写作：
此时 \(\gcd(b,p^{\alpha-cnt})=1\)，我们可以通过第三种情况求出此方程在 \([0,p^{\alpha-cnt})\) 范围中的解的数量。
但这种情况下，由于 \(x\) 的取值范围是 \([0,p^{\alpha})\)，则 \(\dfrac{x}{p^{\frac{cnt}{A}}}\) 的取值范围就是 \([0,p^{\alpha-\frac{cnt}{A}})\)，显然这个的范围要比我们刚才求出来的解的范围要大。
由于在模意义下，上面方程的解每 \(p^{\alpha-cnt}\) 个一循环，我们就能知道，最终要求的答案 \(ans\)，就是 \([0,p^{\alpha-\frac{cnt}{A}})\) 内，长度为 \(p^{\alpha-cnt}\) 的块的数量，再乘以每个块内解的个数。
而这个块数很显然是 \(\dfrac{p^{\alpha-\frac{cnt}{A}}}{p^{\alpha-cnt}}\)，也就是 \(p^{cnt-\frac{cnt}{A}}\)。
所以这种情况下的答案，就是上述方程的解的数量，乘以 \(p^{cnt-\frac{cnt}{A}}\)。
3.\(\gcd(B,p^\alpha)=1\)
我们找到模 \(p^\alpha\) 意义下的某一原根 \(g\)，由于 \(B\) 与 \(p^\alpha\) 互质，故一定存在一个 \(y\)，使：
我们用 BSGS 求解出 \(y\)。
设 \(x=g^{t}\)，则有：
通过指标的性质（其实可以感性理解为通过欧拉定理 \(a^{\varphi(p)}\equiv 1\pmod p\)，左右两边的指数关于 \(\varphi(p^\alpha)\) 同余），有：
这个线性同余方程解的数量，即为原方程解的数量。
当 \(y\bmod \gcd(A,\varphi(p^\alpha))\ne 0\) 时，无解；否则解的个数为 \(\gcd(A,\varphi(p^\alpha))\)。
这样，我们这个超级困难，超级牛逼，超级复杂的逆天题，终于做完了……
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const int N=1e6+10;
const long long INF=0x3f3f3f3f3f3f3f3f;
ll T;
ll A,B,p;
ll pp[N],c[N],t[N],num;
ll qpow(ll a,ll n,ll mod){
ll res=1%mod;
while(n){
if(n&1) res=(res*a)%mod;
a=(a*a)%mod;n>>=1;
}return res;
}
ll gcd(ll __m, ll __n){
while (__n != 0){
ll __t = __m % __n;
__m = __n;
__n = __t;
}return __m;
}
void divide(ll x){
num=0;ll tmp=x;
for(int i=2;i*i<=x;i++){
if(x%i) continue;
pp[++num]=i;c[num]=0;
while(x%i==0) c[num]++,x/=i;
}
if(x!=1) pp[++num]=x,c[num]=1;
for(int i=1;i<=num;i++) t[i]=tmp/pp[i];
return;
}
ll getgen(ll phi,ll n){
for(int i=1;i<=n;i++){
if(gcd(i,n)!=1) continue;
if(qpow(i,phi,n)!=1) continue;
bool is=1;
for(int j=1;j<=num;j++){
if(qpow(i,t[j],n)==1) {
is=0;break;
}
}
if(is) return i;
}return -114514;
}
ll BSGS(ll a,ll b,ll p){
if(a%p==0){
if(b%p==1&&a!=0) return 0;
else if(b%p==0) return 1;
else return -1;
}
map <ll,int> mp; mp.clear();
b%=p;ll t=ceil(sqrt((double)p)),now=b;
for(int j=0;j<t;j++){
if(j) (now*=a)%=p;
mp[now]=j;
}
now=1;a=qpow(a,t,p);
for(int i=0;i<=t;i++){
if(i) (now*=a)%=p;
if(mp.find(now)!=mp.end()&&i*t-mp[now] >=0) return i*t-mp[now];
}return -1;
}
ll calc(ll p,ll alp,ll B){
ll now=qpow(p,alp,INF);
ll b=B%now;
if(b==0){
ll t=(alp-1)/A + 1;
return qpow(p,alp-t,INF);
}
ll cnt=0;
while(b%p==0) cnt++,b/=p;
// printf("p:%lld alp:%lld now:%lld b:%lld cnt:%lld\n",p,alp,now,b,cnt);
if(cnt==0){
ll phi=now - qpow(p,alp-1,INF);
divide(phi);
ll ming=getgen(phi,now);
ll y=BSGS(ming,b,now);
ll ty;
ll tmp=gcd(A,phi);
if(y%tmp) return 0;
return tmp;
}
if(cnt%A) return 0;
return calc(p,alp-cnt,b) * qpow(p,cnt-cnt/A,INF);
}
int main(){
scanf("%lld",&T);
for(int Case=1;Case<=T;Case++){
scanf("%lld%lld%lld",&A,&B,&p);
p=2*p+1;ll res=1;
for(int i=2;i*i<=p;i++){
if(p%i) continue;
ll now=1,alp=0;
while(p%i==0) p/=i,now*=i,alp++;
// ll tmp=calc(i,alp,now);printf("p:%d alp:%lld now:%lld res:%lld\n",i,alp,now,tmp);
res *= calc(i,alp,B);
}
if(p!=1){
res *= calc(p,1,B);
}
printf("%lld\n",res);
}
return 0;
}
- P4139 上帝与集合的正确用法
要求这么一个东西：
的值。
我们有扩展欧拉定理：
故：
然后递归求解 \(2^{2^{2^{\dots}}}\bmod \varphi(p)\) 即可，复杂度 \(O(\log p)\)。
当然可以加个记忆化，可能跑的更快。
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const int N=1e7+10;
int prime[N],tot,v[N],phi[N];
ll T=1,p;
void shai(int n){
phi[1]=1;
for(int i=2;i<=n;i++){
if(v[i]==0){
v[i]=i;prime[++tot]=i;
phi[i]=i-1;
}
for(int j=1;j<=tot;j++){
if(prime[j] > v[i] || prime[j] > n/i) break;
v[i*prime[j]]=prime[j];
if(i%prime[j]==0){
phi[i*prime[j]]=prime[j] * phi[i];
}else{
phi[i*prime[j]]=(prime[j]-1)*phi[i];
}
}
}
}
ll qpow(ll a,ll n,ll mod){
ll res=1%mod;
while(n){
if(n&1) res=(res*a)%mod;
a=(a*a)%mod,n>>=1;
}return res;
}
ll calc(ll p){
if(p==1||p==2) return 0;
ll tmp=calc(phi[p])+phi[p];
return qpow(2,tmp,p);
}
int main(){
shai(N-10);//0.3s
scanf("%lld",&T);
for(int Case=1;Case<=T;Case++){
scanf("%lld",&p);
printf("%lld\n",calc(p));
}
return 0;
}
- BZOJ4454. C Language Practice
给定两个长度分别为 \(1\le n,m\le 2\cdot 10^3\) 的数组 \(a\) 和 \(b\)，求：
满足 \(0\le a_i,b_j\le 10^6\)。
式子推不了一点，遂直接枚举。使用黑科技 \(O(1)\gcd\)，卡常，如过。
如过，遂无提交记录。
点击查看代码
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef unsigned int ll;
const int N=2010,M=1020,maxm=1e6+10,INF=0x3f3f3f3f;
ll T=1,t=1010;
ll a[N],b[N],n,m;
ll prime[maxm],tot;
ll v[maxm],ggcd[N][N],split[maxm][3];
void shai(ll n){
for(ll i=2;i<=n;i++){
if(!v[i]){
v[i]=i,prime[++tot]=i;
}for(int j=1;j<=tot;j++){
if(prime[j] > v[i] || prime[j] > n/i) break;
v[i*prime[j]] = prime[j];
}
}return;
}
void Init(){
for(int i=1;i<=t;i++) ggcd[i][0]=ggcd[0][i]=i;
for(int i=1;i<=t;i++){
for(int j=1;j<=t;j++){
ggcd[i][j]=ggcd[j%i][i];
}
}
split[1][0]=split[1][1]=split[1][2]=1;
for(int i=2;i<=maxm-10;i++){
ll minn=INF,mini;
for(int j=0;j<3;j++){
split[i][j]=split[i/v[i]][j];
if(split[i][j] < minn) minn=split[i][j],mini=j;
}
split[i][mini] *= v[i];
}
}
int Gcd(int x,int y){
if(x<=1010 && y<=1010) return ggcd[x][y];
if(!x || !y) return x+y;
ll res=1;
for(int i=0;i<3;i++){
if(split[x][i]==1) continue;
ll tmp;
if(split[x][i] <= 1010) tmp=ggcd[split[x][i]][y%split[x][i]];
else if(y%split[x][i]==0) tmp=split[x][i];
else tmp=1;
res *= tmp;y/=tmp;
}return res;
}
int main(){
shai(maxm-10);
Init();
cin>>T;
ll res;
ll ans[N],cnt=0;
while(T--){
scanf("%u%u",&n,&m);
for(int i=0;i<n;i++) scanf("%u",&a[i]);
for(int j=0;j<m;j++) scanf("%u",&b[j]);
res=0;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
res += Gcd(a[i],b[j]) ^ i ^ j;
}
}
printf("%u\n",res);
}
return 0;
}
//0.36->6.54
- hdu6209 The Intersection
给定两函数 \(f(x)=\sqrt x,g(x)=\dfrac{k}{x}\)，多次询问给定 \(k\)，求两函数交点的 \(x\) 坐标。
我们联立解方程，有 \(x=k^{\frac{2}{3}}\)。
用 SB 树去逼近就行了。
注意开long double。
- P5172 Sum
给定 \(n,r\)，求：
首先，我们用 SB 树找到一个最逼近 \(\sqrt r\) 的分数，设为 \(\dfrac{a}{b}\)。
于是原式变为：
这个东西的指数看起来和万欧很像，于是我们考虑使用万欧求这个东西。
每个操作序列上维护两个东西：
我们考虑对 \(l,r\) 进行合并，有：
我们跑一遍万欧，输出答案的 \(sum\) 即可。
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define double long double
#define DEBUG
using namespace std;
typedef long long ll;
const long long N=1e16;
ll T=1;
struct node{
ll y,sum;
node() : y(0), sum(0) {};
node operator *(node b){
node a=*this,c;
c.y=a.y + b.y;
if(a.y &1) c.sum = a.sum - b.sum;
else c.sum = a.sum + b.sum;
return c;
}
}U,R,res;
node qpow(node a,ll n){
node res;
while(n){
if(n&1) res = res * a;
a=a*a,n>>=1;
}return res;
}
ll div(ll a,ll b,ll c,ll d){
return ((double)1.0*a*b+c)/d;
}
node calc(ll p,ll q,ll r,ll n,node U,node R){
if(!n) return node();
if(r >= q) return qpow(U,r/q) * calc(p,q,r%q,n,U,R);
if(p >= q) return calc(p%q,q,r,n,U,qpow(U,p/q) * R);
ll m = div(p,n,r,q);
if(!m) return qpow(R,n);
return qpow(R,(q-r-1)/p) * U * calc(q,p,(q-r-1)%p,m-1,R,U) * qpow(R,n-div(q,m,-r-1,p));
}
pair <ll,ll> sbt(ll x){
ll a=0,b=1,c=1,d=0;
ll ra,rb;
ll tmp=sqrt(x);
if(tmp*tmp==x) return MP(tmp,1);
while(1){
ll e=a+c,f=b+d;
if(f>N) break;
if(e*e < f*f*x) a=e,b=f;
else c=e,d=f;
ra=e,rb=f;
}
return MP(ra,rb);
}
ll n,r;
int main(){
scanf("%lld",&T);
U.y=1;R.sum=1;
for(int Case=1;Case<=T;Case++){
cin>>n>>r;
pair<ll,ll> qr=sbt(r);
// cout<<qr.first<<"/"<<qr.second<<endl;
node res=calc(qr.first,qr.second,0,n,U,R);
printf("%lld\n",res.sum);
}
return 0;
}
- PE372 光锥
参考了 beginendzrq 的题解，_ANIG_ 的提示，Qcfff 写的代码。我抄抄抄抄抄抄
给定 \(m,n\)，求：
保证 \(\dfrac{n}{m}\le 500\)。
我们枚举 \(t=\left\lfloor\dfrac{y^2}{x^2}\right\rfloor\)，有：
看一下它的几何含义：
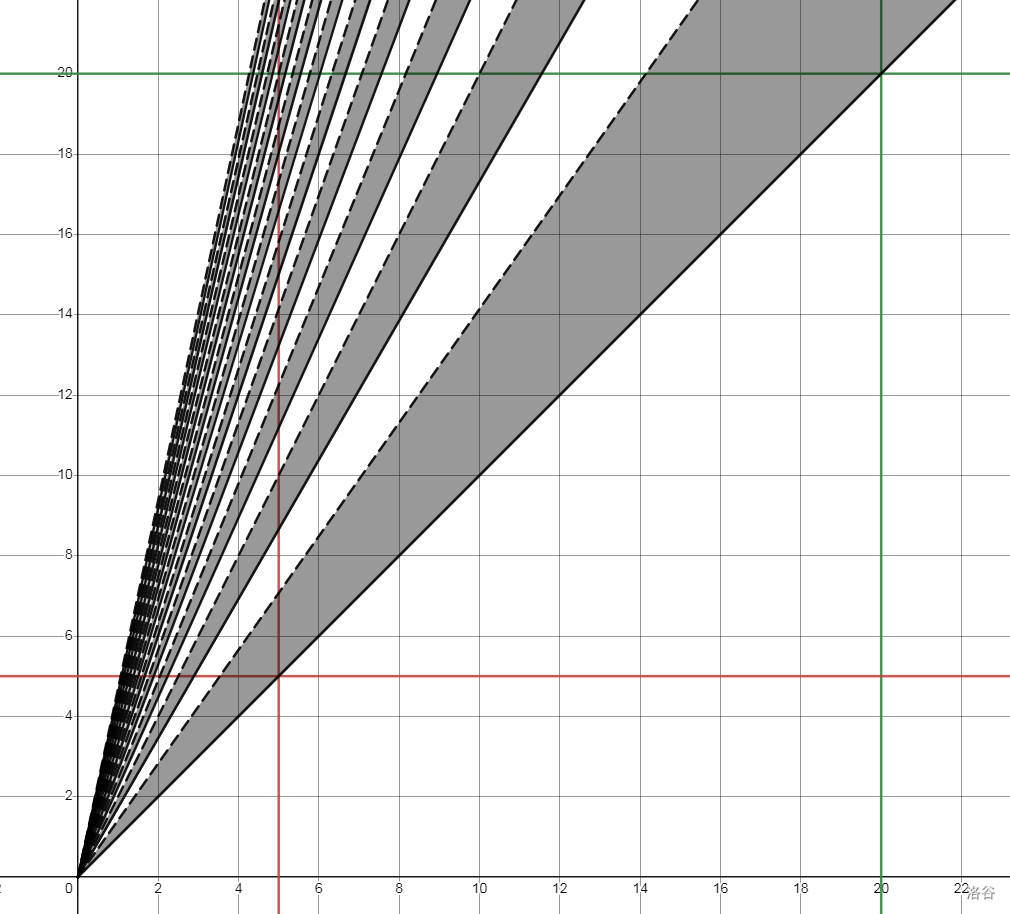
我们要求红绿线围成的正方形里，黑色阴影中的整点数量。
\(t\) 其实是在枚举斜率，每条直线都是一个以 \(\sqrt t\) 为斜率的直线。
我们可以考虑求出每条直线与正方形上边，左边围成的三角形中有多少个点。
以 \(y=\sqrt 2x\) 为例：
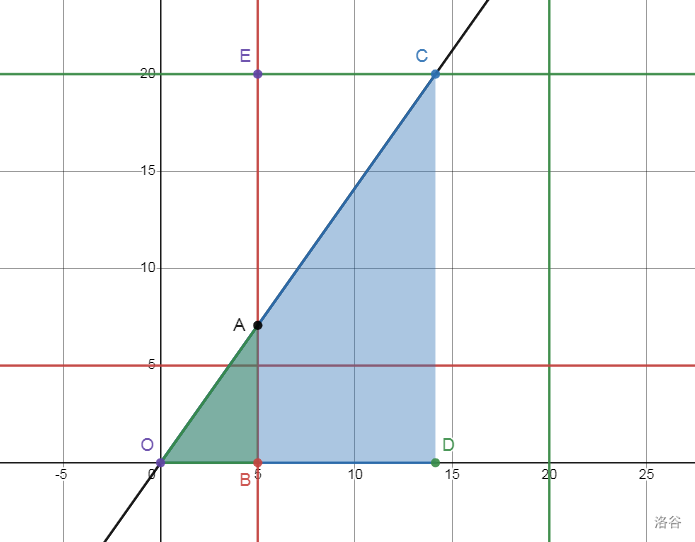
我们分别用万欧求出 \(\triangle OAB\) 中整点个数，记为 \(u\)，再求出 \(\triangle OCD\) 内的整点个数，记为 \(v\)。
\(u-v\) 即为蓝色梯形 \(ABCD\) 中整点个数。
我们再用大长方形 \(BECD\) 中的整点个数，减去 \(u-v\)，就能得到 \(\triangle AEC\) 中的整点个数。
当然我们需要考虑线段 \(AC\) 上的整点个数。
当 \(t\) 不为平方数，上述做法完全可以。
当 \(t\) 为平方数，我们万欧时会计算 \(AC\) 上的整点，而用长方形一减就减没了。于是我们还需要加上直线上的整点数。
具体看代码：
for(int k=1;k<=lim;k++){
ll now=0;
pair <ll,ll> tmp=sbt(k);
ll l=m,r=(double)n/sqrt((double)k);
now += calc(tmp.first,tmp.second,0,r,U,R).sumy;
now -= calc(tmp.first,tmp.second,0,l,U,R).sumy;
now = (r - l ) * (n) - now;
ll qk=sqrt(k);
if(qk*qk==k){
now += (r-l);
}
if(k%2==1) res += now;
else res -= now;
}printf("%lld\n",res);
r 是点 \(C\) 的横坐标，即解方程 \(\begin{cases}y=\sqrt t x\\y=n\end{cases}\) 得 \(x=\dfrac{n}{\sqrt t}\)。
应该很直观了。我们万欧时套个 SB 树板子，把根号变成分数就能算了。
另外，特别鸣鸣鸣鸣鸣鸣鸣鸣鸣鸣鸣鸣谢 Qcfff 想出的做法和实现的代码，我都是抄他的，他真的我哭死呜呜呜
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const long long N=1e15;
ll m,n;
struct node{
ll x,y,sumy;
node() : x(0) , y(0), sumy(0) {};
node operator *(node b){
node a=*this,c;
c.x=a.x + b.x;
c.y=a.y + b.y;
c.sumy = a.sumy + b.sumy + a.y * b.x;
return c;
}
}U,R,res;
node qpow(node a,ll n){
node res;
while(n){
if(n&1) res = res * a;
a=a*a,n>>=1;
}return res;
}
ll div(ll a,ll b,ll c,ll d){
return ((long double)1.0*a*b+c)/d;
}
node calc(ll p,ll q,ll r,ll n,node U,node R){
if(!n) return node();
if(r >= q) return qpow(U,r/q) * calc(p,q,r%q,n,U,R);
if(p >= q) return calc(p%q,q,r,n,U,qpow(U,p/q) * R);
ll m = div(p,n,r,q);
if(!m) return qpow(R,n);
return qpow(R,(q-r-1)/p) * U * calc(q,p,(q-r-1)%p,m-1,R,U) * qpow(R,n-div(q,m,-r-1,p));
}
pair <ll,ll> sbt(ll x){
ll a=0,b=1,c=1,d=0;
ll ra,rb;
ll tmp=sqrt(x);
if(tmp*tmp==x) return MP(tmp,1);
while(1){
ll e=a+c,f=b+d;
if(f>N) break;
if(e*e < f*f*x) a=e,b=f;
else c=e,d=f;
ra=e,rb=f;
}
return MP(ra,rb);
}
int main(){
scanf("%lld%lld",&m,&n);
ll lim=n*n/(m+1)/(m+1),res=0;
cout<<lim<<endl;
U.y=1,R.x=1;
for(int k=1;k<=lim;k++){
ll now=0;
pair <ll,ll> tmp=sbt(k);
ll l=m,r=(double)n/sqrt((double)k);
now += calc(tmp.first,tmp.second,0,r,U,R).sumy;
now -= calc(tmp.first,tmp.second,0,l,U,R).sumy;
now = (r - l ) * (n) - now;
ll qk=sqrt(k);
if(qk*qk==k){
now += (r-l);
}
if(k%2==1) res += now;
else res -= now;
}printf("%lld\n",res);
return 0;
}
