耻辱柱一号
这里记录了 2023.11.26-2023.12.29 期间打的共 32 场 CF 比赛。
但是仍然有很多没写总结,比如第二场到第七场,以及最后的两场「baoyang vs qcf」。先咕着,有空写。
Part 0.场内切题数量统计
第一场「CF1845,Round151」
切三题,ABC。
第二场「CF1841,Round150」
原因:
C:自己写的代码又臭又长,场内切不出来有很大原因是思路想复杂(虽然也能做)导致代码也复杂。
D:补了好久好久,怎么也没想到能把每两条相交的线段合并为一条线段,在转化为一个贪心:按右端点排序,按顺序枚举,能要就要。
E:栈好题,画画图做出来。
总结:三个题里做题时间最短的就是E题,但做题时长是否超出了比赛内的空余时间,我记不得了。
第三场「CF1697,Round130」
第四场「CF1681,Round129」
C:自己写的代码又臭又长,而且打这一场的时候只有一个半小时(当然时间够用的话也切不出来)。还是思路复杂,如果把a和b合并一下,cmp改成两个数的a相等时按照b排序,遍历一遍b是否有序其实就好了,输出方案的话就记录一下idx直接打印不就行了么,非要写的那么复杂
D:搜索,感觉场内应该能切出来但就是一直在做C题,就没去做
E:坏倍增,调了好久,场内绝对切不出来。
总结:还是应该看一遍题,找到哪个最简单去做哪个,不能在一个题上死磕
第五场「CF1709,Round132」
C:直到赛后也没想出来,问了qcf,把问题转化后仍然没做出来,看了题解的逆天做法后写了写过了,但仍然看不懂。
感觉那个把前L个填成
D:纯纯的水题
E:不会dsu on tree,问了cy才会。
总结:仍然是没看好难度,如果直接做D的话肯定能做出来,偏偏去做那个该死的C题,然后还做不出来。
第六场「CF1701,Round131」
切三题,ABC。
第七场「CF1716,Round133」
C:不仅是场内切不出来,补题时也在想一个倍增,结果数组大小应该是3,开成2导致TLE,一直改不出来都要爆炸了,没想到完全可以不用倍增,在正解中发现了TLE原因,才把两种做法都过去,太逆天了!!!
D:他么的一个类似单调队列优化多重背包的,把余数相同的状态做前缀和优化dp都想不出来,脑子不知道在干什么
E:没想到状态数很少,明明搜一遍就能出来的……
总结:三个题罪大恶极,做的时间一个比一个长,场内切不出来是脑子裂开了导致的
第八场「CF1832,Round148」
切三题,ABC。
第九场「CF1680,Round128」
切三题,ABC。
第十场「CF1849,Round152」
切四题,ABCD。
第十一场「CF1861,Round154」
C:一开始读错了题,题读对了之后开始做,想得太简单了,以至于一直错,发现稍微冷静一下应该就能找到做法,偏偏就没找到……
D:dp,补题的时候都做了好久,别提场内了
E:逆天题和逆天结论和逆天猜结论人
总结:补题时间都极长,感觉场内做不出来一是急了,二是真的做不出来
第十二场「CF1860,Round153」
切三题,ABC。
第十三场「CF1837,Round149」
切四题,ABCD(或者说4.5,因为场后马上切出了E)。
第十四场「CF1821,Round147」
切四题,ABCE。
第十五场「CF1792,Round142」
C:咋也没想到二分,硬是在那里想想想,想不出来。
D:好题,好分治,如果场内做的话大概率做得出来
E:逆天题,因数个数我和你拼了!!!
总结:急了,C想不出来纯粹是急了;难度分配不合理,应该做D再做C
第十六场「CF1783,Round141」
C:杀杀杀,场后补题还是杀杀杀,写的极为复杂……
D:简单dp。
E:就在写这个剪贴板的前一天才做出来,记忆犹新,整除分块过不去,正解还想不到,很离谱。
总结:应该先做D题
第十七场「CF1882,Codeforces Round 899」
切三题,ABC
第十八场「CF1739,Round136」
切三题,ABC。
第十九场「CF1721,Round134」
切四题,ABCD。
第二十场「CF1661,Round126」
C:逆天提,分讨讨论不出来,还浪费时间硬想。
D:简单枚举
E:还没做
总结:应该先做D题。
第二十一场「CF1814,Round146」
切三题,ABC。
第二十二场「CF1809,Round145」
原因:跑神了!!!你在干什么啊!!!!!!!!
第二十三场「CF1796,Round144」
原因:单纯时间不够用啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊!!!!!!!!!!!!!!!!!!!!!
第二十五场「CF1767,Round140」
切三题,ABD。
第二十六场「CF1766,Round139」
切三题,ABC。
第二十七场「CF1749,Round138」
切四题,ABCD。
第二十八场「CF1743,Round137」
切四题,ABCD。
第二十九场「CF1728,Round135」
第三十一场「baoyang vs qcf round 1」
切三题,ABD。
C题纯纯大水题为什么不做啊啊啊啊!!!被qcf生吃了!!!
第三十二场「baoyang vs qcf round 2」
切两题,AB
孬坛B题,逆天构造,被狠狠地诈骗。
为什么C题的st表寄掉了啊啊啊啊啊啊啊啊!!!
Part 1.第一场~第十场
第一场-CF1845
超级大分讨,慢慢分类慢慢做就出来了。
仍然是分讨,慢慢分类慢慢做就出来了。
记
然后从
咕咕咕咕咕咕咕咕
咕咕咕咕咕咕咕咕
第二场-CF1841-第七场
第八场-CF1832
如果原串从第
排个序,算个前缀和,枚举
把序列
当时做的时候连如何把序列划分成上述的段都不会写了。
代码底力和基本功还是太低了!还是得多练练!菜就多练练!
思考时间过长+冷宫常住人口。
非常好题目,爱来自河的南方。
想了好久原问题,不会做;试了试
回来之后试了试,通过考虑
然后又试了试
于是就试了
具体地说,先把
若
若
此时
若此时
否则就把
然后试着优化,提前预处理出
就可以做成
思考时间过长+冷宫常住人口
非常不好评价的组合数dp,借助了蓝书上的一个递推式做出来的
然后记
然后就做完了。
第九场-CF1680
区间相交就是相交处的最左端,不交就是
找到一个最小的矩形,能够包围所有的机器人,若该矩形的左上角是机器人就 YES,否则就NO。
先把字符串最前面和最后面的
把剩余的部分看做连续的
耻辱原因是写得太复杂了,以至于自己本人隔几天就看不懂了。
思考时间过长+冷宫常住人口+未补
思考时间过长。
又是传奇场,耻辱柱三连。
考虑了一个贪心,然后测了几组没毛病,交了,挂了,测试点输出来发现假了。
然后开始考虑一个dp,考虑了一个
所谓收割就是从某个
然后就分别让第一行和第二行在上,然后跑一遍这个dp(转移式极其抽象,有一群魔术数字,不写出来了)。
很抽象地过去了。
第十场-CF1849
如果
否则的话所有夹心都能用,面包用不完,输出
当可以开始杀死某一只怪物时,所有的怪物肯定都已经残血了(能一刀秒),那就把所有怪物的血量 模
字符串哈希,用 set 存哈希值,这个题只用
好像并不是很耻辱,但思考时间不短
做法就是找到好几个有数的段,对于每个段:
存在2就意味着该段染一下后两边的0都能染
不存在2就意味着该段只能然左右两个0之一
然后从左往右贪心地往左染就行了
思考时间过长
乱用启发式合并发现需要写八个二分,后来想了想发现只要四个二分,但是太逆天了!不会写!
于是想到了一个线段树的做法:枚举一个
我们维护一个数组
考虑
先考虑
考虑
经过一番思考可以发现
对于以
而对于 以
再考虑
考虑
经过一番思考可以发现
对于以
而对于 以
经过以上讨论,发现
part 2.第十一场~第二十场
第十一场-CF1861
所以判断一下
(以上做法是伟大的 Qcf 告诉我的,我是把所有两位质数存进 map,枚举两个位置做的)
如果存在一个位置
场内切不出来真的是太孬坛了。
读错题了,以为是1升序0降序,做了好久好久,发现死掉了。
一定要读准题啊!读明白了再做题!!!!!
不难发现序列一定是由一段有序段和一段无序段拼起来,于是用两个变量记录一下有序段和无序段的位置,一通模拟即可(不展开写了,因为写这篇博客时已经看不懂我写的代码了)。
思考时间过长
仍然是晚上读错题了,以为x>=0,想了一个早读的假做法,结果一会机房发现消愁了
记
考虑转移:
不方便慢慢解释了,而且这个状态本身就很迷惑,这个转移式也很迷惑……
思考时间过长+冷宫常住人口
神了这场比赛,CDE都被我钉在耻辱柱上
考虑了
结果寄掉了,连
后来思考了好久,发现了一个好玩的东西:当一个串贡献为
于是考虑
首先
对于
考虑有哪些重复的可能性,令
所以对于每个
这里解释一下为什么要多乘一个
这里列一下总转移式:
第十二场-CF1860
如果
否则就输出
大分讨,不展开写了,太难受了。
对于第
我们把必胜点记为
所以我们在值域上建两颗树状数组,直接维护就行了。
思考时间过长+冷宫常住人口+未补
思考时间过长+冷宫常住人口+未补
第十三场-CF1837
如果
把
如果
如果原序列本身合法或逆合法,就输出
否则一定能把原序列分成两部分,一部分是正合法,另一部分是逆合法。
染个色标记一下就行了。
假设当前是第
考虑当前内定的会不会使它们之间互相争斗,以判断无解。
把这一轮还没有被内定的这些人填进去,答案累乘一下就OK了。
第十四场-CF1821
首位的
乘起来就好了。
先找到一对
然后只要
最后输出
枚举这个剩余的字符是谁(
然后把原串分成几个交替的「由除了
把所有的操作次数取
思考时间过长+冷宫常住人口+未补
先思考对于一个给定的字符串,怎么删会使代价最小。
可以分治地考虑:记原串是第
假设当前是第
所以为了最小化代价,就要尽可能地使原串中,深度最大的合法段深度减小。
因为
每一次先找到一个最长的合法段,记为
这样进行
第十五场-CF1792
排个序,不停地查看
第一类直接开演,演完了都是优的。
第二类和第三类可以交替着演,这样可以各演
剩余的能演就演,演不了拉倒。
纯纯的孬坛(指我自己),就是一个贪心+二分,咋就想不出来???
还被狠狠地诈骗,真的看不懂一个小时到底在想什么
做法:二分操作次数,假如当前二分值为
此时看一下这个序列有没有序,有序的话
12.20一稿:
浪费了四个小时,罪大恶极。
原因是蓝书上的一句话:一个整数
所以我就觉得
我甚至不对这个结论产生怀疑!!!!!甚至不去打个程序验证一下约数个数!!!!!!
12.21,AC后二稿:
早上想出正解了,以为错了就没写,看见qcf去问了,导致急了,马上就发现我想出来的是正解,飞快的写完了。
解法:既然知道约数个数只有
紧接着是一个极其巧妙的转换:把「最小行数」转化为「最大列数」,就方便进行 dp 转移了。
问题转化后就是:对于
初值:
形象地,把转移看做一个 DAG 图,对于一个因数
使用 bfs 进行转移:假设当前因数为
进行转移:
同时,我们让
突然意识到,其实我就是把有向图拓扑序遍历的过程说了一遍……
最后统计答案,对于
第十六场-CF1783
先从大到小排序,找到存不存在一个
而但凡存在一个这样的
填法就是按照
光是这一点我都想了半天怎么构造,然后想出来后傻乎乎地写了个深搜,让它旋转地绕圈地走,浪费大把时间。
知道这个之后我们完全可以这么走: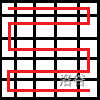 就行了……
就行了……
思考时间过长+想复杂了
曾经在这里发了电,太逆天了所以删了。
我试用了一个及其复杂的做法,就是先贪心,能杀就杀,如果还剩一发,只能再多杀一个人,我其实就知道了我一共能杀多少人。
找到那个和我杀的人数量相同的人,把他杀了就行;找不到就摆。
从12.22开始做,最开始想了个
具体来说是这样的:对于每个
若
若
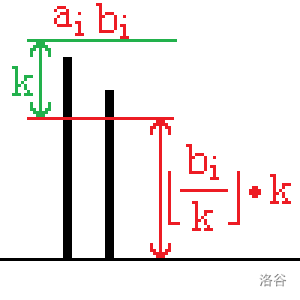
然后分母可以整除分块,每一块内的分母都相等,直接算就行了,但常数巨大且卡不掉,暴死。
然后就各种想,各种不会,一直想来想去想不出来咋做,极为焦虑地过完了这一周。
最接近答案的成果是推出了一个东西:
对于
去一下分母,就成了
然后就可以
第十七场-CF1882
最好是填一个
这破题当成图论做也真的是逆天。
删掉每个数会使哪些数连带着被删,用这个关系建有向图,从每个点开始 dfs,就行了。
感觉不如枚举,但不会枚举。
如果第一张是正数的话,可以先放着不管,总有一种取法,使这张牌之后的所有正数牌都可以取到。
否则,第三张牌及以后的正数牌总能取到,第一张和第二张要么都要,要么都不要,看那种价值更大就行。
小换根 dp。
通过手玩样例,发现一个贪心策略:对于一个节点
则可以先把 每个
然后先从
转移式:
开始换根!记
转移式:
具体的含义为:第一行:把
第二行:把
第三遍:记
计算式:
深搜搜一遍就行了。
第十八场-CF1739
枚举并 check 一下,没啥好说的。
模拟一遍
如果
枚举一遍后如果没有出现任何这样的问题,就唯一确定了。
假设
这个的正确性可以尝试手玩玩出来,写这篇博客时已经距离我玩出来的时候太远了,所以我也没办法解释这玩意的正确性了……
任何时候平局只有一种可能,所以 Bob 赢的方案数 就是
第十九场-CF1721
手玩几组,输出规律即可。
先写了广搜,但由于没有保证
所以其实只需要看一看激光会不会挡住路,挡住了就是
我们维护一个
对于每个
如果此时
考虑从高位到低位枚举,最开始序列被分成
对于每一段,找到
如果两者相等,就把这一位是
如果所有的段的这一位都满足如上条件,那么
不停地分就行了。
非常好题目,算是看了半个题解。意思是说kmp忘了咋写了,于是翻了翻蓝书。
先把
然后就是把询问排序后不停地分治,可以省略很多次重复计算
这样就可以高效地处理询问了!这个做法和曾经的 Fixed Prefix Permutations CF1792D 这道题非常像,用的是相同的思想!
第二十场-CF1661
每一对数都尝试交换,看换和不换那个更小。
因为
然后预处理一下
先寻找一个最终所有树相等的一个高度,记为
记录
对于每一个
-
如果
-
如果
为了用完剩余的
- 如果
我们可以每操作四次,
如果
如果
这剩下的一个
如果如果
剩下的
这种大情况下,总操作次数就是:
而关于
区间减等差数列,要求操作次数最小。
倒着考虑,维护一个
此时
这样枚举几遍就行了。
Part 3.第二十一场~第三十二场
第二十一场-CF1814
分类讨论,若
若
其他情况就是 YES 了。
最开始尝试把
然后马上就找到了hack:a=1,b=11。
然后尝试枚举
做完后拐回来一看,发现题目本质就是让你找一个
其实等同于求这个的最小值:
扔进 desmos 一看,我趣!对勾函数!
事实上,把上取整去掉,这就是个对勾函数,当
戴上了上取整咋办捏?充分发扬人类智慧可知正确决策距离
大水题,序列倒序排序一下,当前数让当前完成时间较少的那个机器完成,分类一下输出就行了。
为什么不和B题对调一下?
好题,写成题解了:CF1814E Chain Chips 题解。
第二十二场-CF1809
全相同为
曾经我在这里大骂一通这个题,后来发现没什么实质性作用,就删了。
明确一下,这题一共有两种填法:
第一种: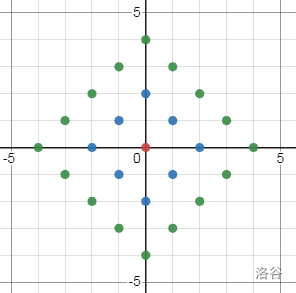
前
第二种: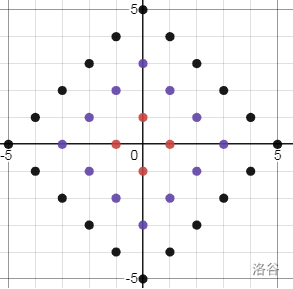
前
两种染法取
非常好构造题,先二分找到一个最大的
此时
先想一个弱化版问题:如果只有删数运算,怎么删花费最小。
枚举一个
段内的
而带上了交换操作后,仍然这样枚举,当枚举到
若
同理,此时若
统计一下每个
在每个
第二十三场-CF1796
把这个FB的字符串的前
第一次做这个题的时候我甚至还在枚举起点时
如果两个串有相同的长度为2的子段(记为 *S* 。
否则如果两个串第一位相同(记为 s1* 。
否则如果两个串最末位相同(记为 *s2 。
否则无解。
从最开始的
当这个集合的最小元素选
此时,我们考虑左端点最大为多少时,乘以
每一个这样的的区间都可以为
根据
考虑换完之后左端点最大为多少,显然是
每一个换成
最后输出答案为
差点就场切了,非常可惜。
for(int i=1;i<=n;i++){
for(int j=0;j<=min(k,(ll)i);j++){
ll tmp1=0,tmp2=0;
if(i>j) tmp1=a[i]-x + max(dp[i-1][j],0ll);
if(j>0) tmp2=a[i]+x + max(dp[i-1][j-1],0ll);
dp[i][j]=max(max(tmp1,tmp2),0ll);
if(n-i>=k-j)ans=max(ans,dp[i][j]);
}
}printf("%lld\n",ans);
有很多细节,因此没有场切
1.只有当
2.只有当
3.统计答案的时机很怪,当
放在最前头:金色传说!!!场内切了五个!!!
把
若
先把所有不覆盖
然后算出每个点被覆盖的次数,可以差分也可以直接遍历(毕竟
枚举除了
对于每一杯茶,二分查找出它被喝完的时那个人。
具体来说,对于第
然后使用一个 double 类型的差分数组,在
记
最后把差分数组求前缀和,第
看着吓唬人,实则纯纯的水题。
一共有
而因为保证了染蓝色和染红色的数量相同,所以可以给某
此时染色给答案的贡献为
此时问题就转化成了每个三角形选出一条边,使得选出的边之和最小。显然,选法就是每个三角形选出其中三条边的最小值。
而对于某个三角形,如果有多条最小值边,则可以选择任意一条,所以此时对答案的贡献为
总答案就是
这是我在这么多场比赛第一次把一个 dp 分成左贡献和右贡献。
记
记
外层循环枚举
碰到第
所以总转移式就是:
统计答案:
好!!!!!!!!
第二十五场-CF1767
当这个三角形是直角三角形,且直角是横平竖直时,输出NO。
那就枚举某一个顶点是直角顶点,根据坐标判断一下就行了。
把
这样遍历一遍之后的
这题没补,先写一下现有的思路,方便以后再补。
首先把所有
这些段从
每一个
此时若
然后不会了!!!
记
讨论
当且仅当存在一个
如何判断相交不相交?
他们需要多少个人呢?假如前
然后 dp 地统计答案就好了。
第二十六场-CF1766
用前缀和预处理一下
枚举,把当前出现过的长度为二的子串扔进一个 map 里。然后查找当前
枚举
乱搞一下就行了。
显然,如果当前
如果
对于剩余的情况,令
这意味着我们要找到
A后二编:事实上,我们只需要枚举
如何快速找到
第二十七场-CF1749
知道
我最开始甚至在链表模拟……
原理就是所有的
为了让
二分答案,假设当前答案为
因为
假设当前是第
第一个人从当前没有被删除的数中,找到最大的
第二个人给当前没有被删除的数中,最小的数加上
模拟一遍,看第一个人能否删完
如果考虑孬序列的个数不好考虑的话,正难则反,考虑不孬的序列个数,记为
考虑一下不孬的序列实质是什么,显然就是满足这样的序列:对于每个
将
所以当序列长度为
此时我们就可以表示答案了:
第二十八场-CF1743
第一位放
不读题导致的,以为每个板子都可以往左或往右,浪费大把时间。
把原序列划分为多个连续的
对于第
数据随机,所以乱搞就行。
找到最左边第一个
分别把
第二十九场-CF1728
输出最大值所在位置。
显然答案最大就是
如果
如果
转化题意:给定两个可重集合,是用最少的操作次数,使得两个集合相等。
先把
对于不匹配的,用操作把
对于剩下的,不为
赛后五秒钟切出来。如何评价?
首先可以明确一点,手玩几组发现Bob 无论如何也赢不了(至于为啥我也不知道)。所以 Bob 所能做的就是尽可能平局。
设
若
若
设
转移方程:
当
当
最后如果
第三十场-CF1671
把
把原序列划分为几个连续的斜率为一的段,对端的个数进行讨论。
只有一段显然可以;只有两段的话交点处的差
对于某个时刻来说,想要买更多的糖,肯定是挑价格最便宜的几包来买,所以随着日子的增多,购买方案只会不停地减少其中的最大值者。
所以可以先排个序,求个前缀和,对于每个前缀和计算
记最大的
这个东西枚举一遍就算出来了,这题就做完了。
记
然后考虑
三种方法对分数的影响分别是加上:
毕竟这两段不能同时占用 序列最前头或序列最后头,所以分类讨论一下就行了。
放在最前头:div.2 的比赛,A
非常简单 dp,记
如果以
每个节点的子树能否本质上相同,可以预处理:把每个节点的左右儿子交换成 左小右大,就可以直接通过两颗子树的前序遍历是否相等来判断是否本质相同了。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具