类欧,万欧,SB 树
一. 类欧几里得算法
复述题解:
我们记 \(f(a,b,c,n)=\sum\limits_{i=0}^{n}\Big\lfloor \dfrac{ai+b}{c} \Big\rfloor\,,\ g(a,b,c,n)=\sum\limits_{i=0}^{n}i\Big\lfloor \dfrac{ai+b}{c} \Big\rfloor\,,\ h(a,b,c,n)=\sum\limits_{i=0}^{n}{\Big\lfloor \dfrac{ai+b}{c} \Big\rfloor}^2\)
第零部分·概况
基本上就是先把 \(a\) 和 \(b\) 对 \(c\) 取模,看看对答案的贡献,然后再推推式子,推出来可以递归求解的一个过程。
我们令两个神秘数字:
第一部分·求解 \(f\)
取模部分
推式子部分
第二部分·求解 \(g\)
取模部分
推式子部分
第三部分·求解 \(h\)
取模部分
推式子部分
这里要用到一个神秘的东西:
终于!!!我写完了这刘拓世!!!我真的自己也不想再看它一眼了……
我们发现这三个函数的计算过程都是在递归,而且传下去的内容也一样,于是我们把这三个的计算扔进一个函数里,一同计算。
这样这个模板题就做完了,提交记录
以上便是我此时此刻对这玩意的全部理解,只会模板题。
2.万能欧几里得算法
强烈推荐这位大佬写的博客:apjifengc's blog,以及另一位大佬的博客:ix35_
本文思路与上述博客思路一致,不过举的例子换了一下,并加入一些自己的理解。
类欧几里得算法,是一类可以通过辗转相除的方式递归解决的问题,由于其复杂度分析与欧几里得算法一致,所以称为类欧几里得算法。其中,类欧最常见的形式是直线下整点数问题,即求 \(y=\left\lfloor\dfrac{px+r}{q}\right\rfloor\) 这个函数的相关问题,如 \(\sum y\),\(\sum y^2\),\(\sum xy\)。而传统的类欧推导方法多数繁琐复杂,式子长,难推导且难记。这时候,我们有一个算法,叫万能欧几里得算法,他将上述问题进行抽象化,并给出了这类问题的一个通用解法。不过,两者的思想是完全相同的。
我们不再过多赘述类欧几里得算法,这里直接开始介绍万能欧几里得算法,它的思想与上述算法思想一模一样,但用另一种方法抽象这个问题:
给定二维坐标系上的一次函数 \(y=\dfrac{px+r}{q}\)。我们维护一个向量 \(v\),考虑这个函数每次向右穿过网格的竖线时,给 \(v\) 乘上一个矩阵 \(R\);每次向上穿过网格的横线时,给 \(v\) 乘上一个矩阵 \(U\)。若恰好经过一个整点,那么先乘 \(U\) 再乘 \(R\)。若 \(x\in[1,n]\),求最后的向量 \(v\)。
例如求 \(\sum y\),我们可以维护矩阵 \([y,\sum y,1]\),考虑 \(U\) 和 \(R\) 分别是什么。
- 向上穿过网格时,\(y\) 会增加 \(1\),即:
- 向右穿过网格时,\(\sum y\) 会增加 \(y\),即:
我们全篇以这个函数举例子:\(y=\dfrac{4x+8}{3}\) 在 \(x\in[1,n]\) 下的整点数。
我们这里附赠一张图片。
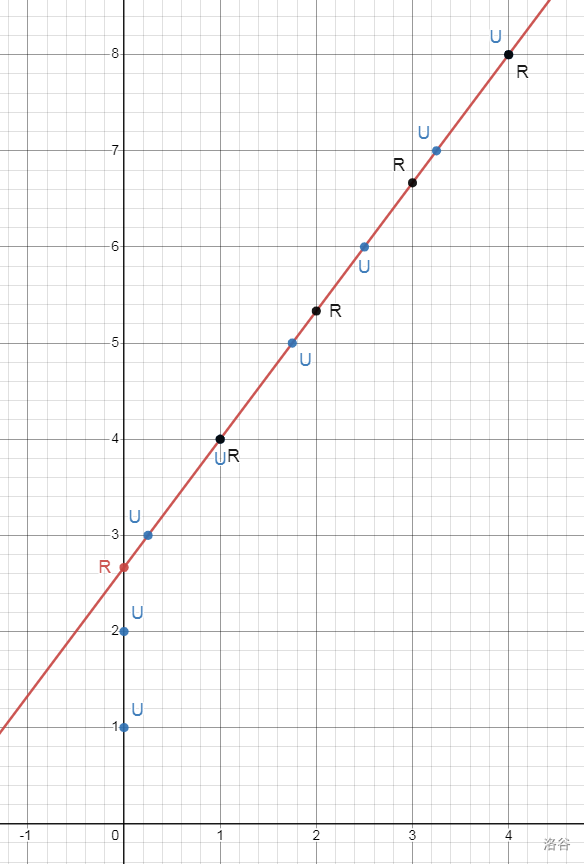
我们令开始 \(v=\begin{bmatrix}0&0&1\end{bmatrix}\),则最终的 \(v\) 应乘上:
可以参照图片上标出来的 \(U\) 和 \(R\) 来理解。
注意,我们这里标注出了一个红色的 \(R\),这个 \(R\) 并不在真正的对 \(v\) 的计算中,而是为了区分而标出来的第 \(0\) 个 \(R\),这个红色的 \(R {\color{red}\text{ 不存在}}\) 。
于是乎,我们要求的其实就是上面这个式子。
首先问题相当于在说,求在第 \(i\) 个 \(R\) 前面,一共(注意不是两个 \(R\) 之间)有 \(\left\lfloor\dfrac{pi+r}{q}\right\rfloor\) 个 \(U\),一共有 \(n\) 个 \(R\)(注意,这里第零个 \(R\) 不存在,标出来是为了表示前面\({\color{red}\text{存在 }}\left\lfloor\dfrac{p\cdot 0+r}{q}\right\rfloor\) 个 \(U\)),且最后一个为 \(R\) 的矩阵乘积。
我们可以考虑类比类欧的做法,解决这个问题。
我们定义函数 \(\operatorname{calc}(p,q,r,n,U,R)\) 为上述问题的答案。
例子中即为求 \(\operatorname{calc}(4,3,8,4,U,R)=UU{\color{red}R}UURURURUUR\)。
(1)
若 \(r\ge q\),那么就先把第 \(0\) 个 \(\color{red}R\) 前面的 \(\left\lfloor\dfrac{p\cdot 0+r}{q}\right\rfloor=\left\lfloor\dfrac{r}{q}\right\rfloor\) 个 \(U\) 乘起来。
放到例子中,表达的就是:
我们相当于把函数 \(y=\dfrac{4x+8}{3}\) 变成了 \(y=\dfrac{4x+2}{3}\),并且通过手玩,发现 \(\operatorname{calc}(4,3,2,4,U,R)\) 正好就是上式中 \(U^2\) 后面的东西,即:
我们形式化地,用 \(\operatorname{calc}\) 表达出上述意思:
例子中,表达了:
(2)
若 \(p\ge q\),那么每两个 \(R\) 之间至少有 \(\left\lfloor\dfrac{p}{q}\right\rfloor\) 个 \(U\)(包括第零个 \(\color{red}R\) 和第一个 \(R\) 之间),我们可以把这些 \(U\) 和它们后面的 \(R\) 合并。
我们以例子说明,例子中 \(\left\lfloor\dfrac{p}{q}\right\rfloor=\left\lfloor\dfrac{4}{3}\right\rfloor=1\),即每两个 \(R\) 之间至少有 \(1\) 个 \(U\),于是我们这样进行“分组”(合并):
然后我们令 \({\color{blue}R'}=U^{\lfloor\frac{p}{q}\rfloor}R\),例子中为 \(R'=UR\),带入,有:
这样合并后,原本的每个 \(R\) 前面剩下的一共的 \(U\) 的数量为:
这就意味着,我们会有函数 \(\operatorname{calc}(p\bmod q,q,r,n,U,{\color{blue}R'})\),正好对应了上面最终推出来的式子。
这就意味着,我们有(把 \({\color{blue}R'}=U^{\lfloor\frac{p}{q}\rfloor}R\) 带入):
例子中的具体体现为:
这下,我们就把函数 \(y=\dfrac{4x+2}{3}\) 转化成了 \(y=\dfrac{x+2}{3}\).
(3)
我们已经把所有的 \(r\ge q\),\(p\ge q\) 的情况,转化为 \(r<q\),\(p<q\) 的情况了。
接下来,我们要干一件大事:把 \(U\) 和 \(R\) 互换!
这里我们换一个例子,以便更好的理解一些弊端。
我们换成 \(y=\dfrac{x+1}{4}\)。
有图有真相,我们把图放出来:
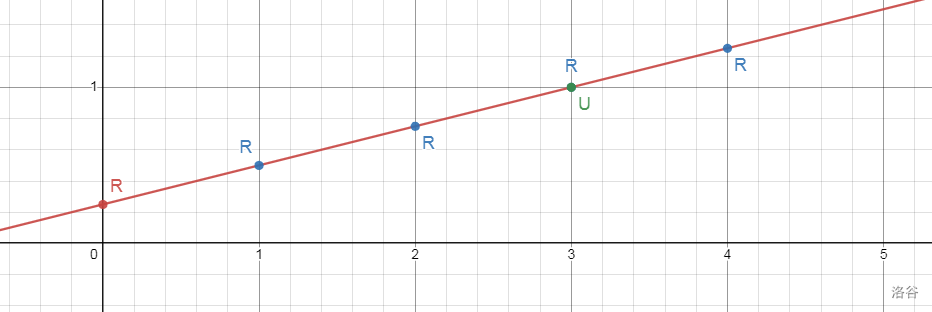
就能写出操作序列了:
考虑将 \(U\) 和 \(R\) 翻转后,我们需要一个 \(\operatorname{calc}(?,?,?,?,R,U)\) 来拟合这个操作序列。我们记翻转后的两种为 \(U',R'\)。
我们先考虑最后一共有多少个 \(U'\),显然就是现在的 \(R\) 的数量,为 \(m=\left\lfloor\dfrac{pn+r}{q}\right\rfloor\),我们这里记为 \(m\)。
我们考虑第 \(y\) 个 \(U'\) 前面有多少个 \(R'\),即为现在的第 \(y\) 个 \(R'\) 前面有多少个 \(U\),容易发现这等同于满足 \(y>\left\lfloor\dfrac{px+r}{q}\right\rfloor\) 的最大整数 \(x\)。推式子,可以得出:
于是乎,我们翻转后就变成了 \(\operatorname{calc}(p,q,r,n,U,R)\rightarrow\operatorname{calc}(q,p,-r-1,m,R,U)\),但显然这是不对的。
我们拿现有的例子来说:
这里出现了两个问题:首先是 \(r\) 为负数我们处理不了,其次是最后一个矩阵是 \(U'\) 不是 \(R'\),不符合定义。我们依次结局。
第一个问题
我们可以把原本的第一段 \(R^iU\),也就是翻转后的第一段 \(U'^iR'\) 单独拿出来处理。这一段的 \(R\) 的数量为 \(\left\lfloor\dfrac{q-r-1}{p}\right\rfloor\)。
第二个问题
我们可以把最后一段 \(R^i\),也就是翻转后的最后一段 \(U'^i\) 单独拿出来处理。这一段 \(R\) 的数量为原本的 \(R\) 的总数,即 \(n\),减去最后一个 \(U\) 前面的 \(R\) 的数量,即 \(\left\lfloor\dfrac{qm-r-1}{p}\right\rfloor\),合起来就是:
由于最前面去掉了 \(\left\lfloor\dfrac{q-r-1}{q}\right\rfloor\) 个 \(R\) 和一个 \(U\),我们现在第 \(x\) 个 \(U\) 前面一共的 \(R\) 的总数就成了:
此时还剩下 \(m-1\) 个 \(R\),所以有:
当然有边界情况,即当 \(m=0\),有:
用例子来体现,就是:
我们计算 \(m=\left\lfloor\dfrac{pn+r}{q}\right\rfloor=1\)
中间那部分就是:
正好啥也没有!
这样就OK了!!
接下来,写一下模板题的题解。
我们定义一个结构体 node 来存放一段操作序列维护的信息。
我们先明确一下,一个 \(U\) 和一个 \(R\) 的实际意义:
\(U\) 代表一种抬升,即把 \(y\) 坐标加一。
\(R\) 代表一种统计,或者说一种右移,即此时此刻,\(x\) 为当前值的 \(y\) 已经加到最高了,我们统计一次答案后使 \(x\) 加一,并使 \(y\) 坐标不变。
所以其实可以看成有一个点在坐标轴上,遇到 \(U\) 就上移,遇到 \(R\) 就右移,并统计答案。
下面我们均把「遇到一个 \(R\) 时」称为「统计时」。
我们令 \(y=\left\lfloor\dfrac{px+r}{q}\right\rfloor\),我们一个 node 中要维护以下六个信息:
\(X\),代表当前遇到过的 \(R\) 的个数,或者说我们正在填 \(x=X\) 这一列。每次统计时,\(X\leftarrow X+1\)。(先于后面所有变量进行)
\(Y\),代表当前遇到过的 \(U\) 的个数,或者说我们填的高度。每次遇到 \(U\) 时,\(Y\leftarrow Y+1\)。
\(\sum x\),每次统计时,\(\sum x\leftarrow\sum x+X\)。所以假如当前一共遇到了 \(k\) 个 \(R\),易发现这个变量其实就是: \(1+2+\dots+k=\dfrac{k(k+1)}{2}\)。
\(\sum y\),每次统计时,\(\sum y \leftarrow \sum y + Y\)。
\(\sum y^2\),每次统计时,\(\sum y^2 \leftarrow \sum y^2 + Y^2\)。
\(\sum xy\),每次统计时,\(\sum y^2\leftarrow\sum xy + xy\)。
我们单独一个 \(U\) 和单独一个 \(R\) 也是一个操作序列,我们需要定义它们的状态。
\(U\):\(Y=1\)。
\(R\):\(X=1\),\(\sum x=1\)。(因为单独一个 \(R\) 也是在啥也没有的基础上进行了一次统计,故它的这两个变量有值)
接下来。我们考虑两段操作序列合并时发生了什么。
以角标 \(l\) 和 \(r\) 来区分两者的变量。(未加角标就是合并后的值)
实现程序时应按照接下来六行公式的顺序进行操作。
我们把 node 之间的乘法重载为这个东西,然后跑一遍就好了。
注意这里求的是从 \(0\) 开始,而万能欧是从 \(1\) 开始,故最终还要加上 \(x=0\) 时的贡献。
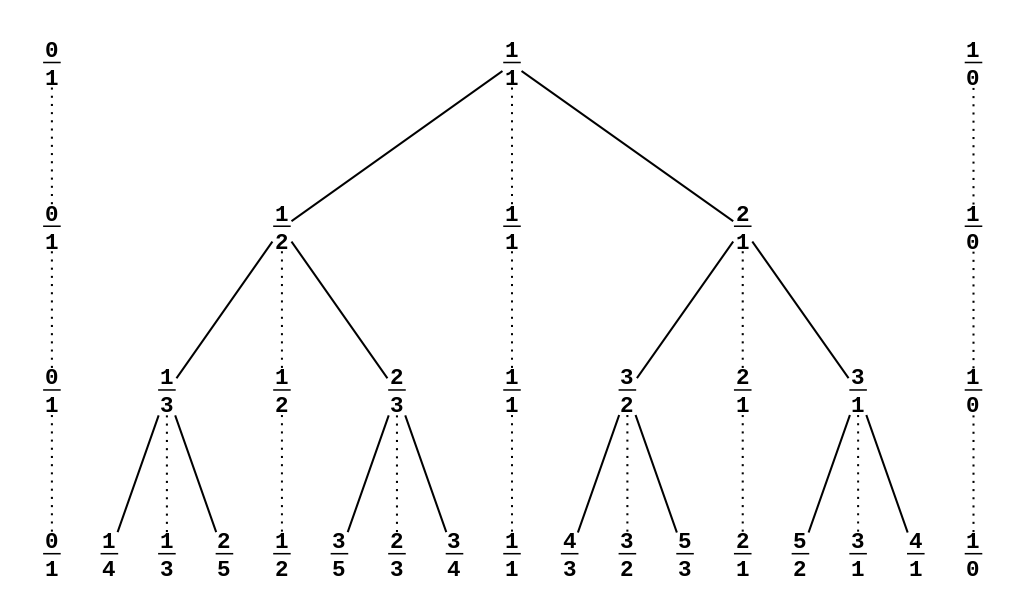
三.SB 树
全称 Stern–Brocot 树。
可以求一个逼近某正小数的最近有理数。
主要依据一个思想:
我们取:
然后依据此思想,二分查找即可。
这颗“树”长这个模样:(图来自oiwiki)
核心代码:
pair <ll,ll> fnd(double x){
ll a=0,b=1,c=1,d=0;
ll rese=0,resf=1;
double mx=x;
bool fl=0;
while(1){
double e=a+c,f=b+d,t=e/f;
if(e>m||f>n) break;
if(fabs(t - x) == mx) fl=1;
if(fabs(t - x) < mx){
rese=e,resf=f;fl=0;
mx=fabs(t-x);
if(mx==0) break;
}
if(t < x) a=e,b=f;
else c=e,d=f;
}
return make_pair(rese,resf);
}
四.例题
- P5172 Sum
给定 \(n,r\),求:
首先,我们用 SB 树找到一个最逼近 \(\sqrt r\) 的分数,设为 \(\dfrac{a}{b}\)。
于是原式变为:
这个东西的指数看起来和万欧很像,于是我们考虑使用万欧求这个东西。
每个操作序列上维护两个东西:
我们考虑对 \(l,r\) 进行合并,有:
我们跑一遍万欧,输出答案的 \(sum\) 即可。
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define double long double
#define DEBUG
using namespace std;
typedef long long ll;
const long long N=1e16;
ll T=1;
struct node{
ll y,sum;
node() : y(0), sum(0) {};
node operator *(node b){
node a=*this,c;
c.y=a.y + b.y;
if(a.y &1) c.sum = a.sum - b.sum;
else c.sum = a.sum + b.sum;
return c;
}
}U,R,res;
node qpow(node a,ll n){
node res;
while(n){
if(n&1) res = res * a;
a=a*a,n>>=1;
}return res;
}
ll div(ll a,ll b,ll c,ll d){
return ((double)1.0*a*b+c)/d;
}
node calc(ll p,ll q,ll r,ll n,node U,node R){
if(!n) return node();
if(r >= q) return qpow(U,r/q) * calc(p,q,r%q,n,U,R);
if(p >= q) return calc(p%q,q,r,n,U,qpow(U,p/q) * R);
ll m = div(p,n,r,q);
if(!m) return qpow(R,n);
return qpow(R,(q-r-1)/p) * U * calc(q,p,(q-r-1)%p,m-1,R,U) * qpow(R,n-div(q,m,-r-1,p));
}
pair <ll,ll> sbt(ll x){
ll a=0,b=1,c=1,d=0;
ll ra,rb;
ll tmp=sqrt(x);
if(tmp*tmp==x) return MP(tmp,1);
while(1){
ll e=a+c,f=b+d;
if(f>N) break;
if(e*e < f*f*x) a=e,b=f;
else c=e,d=f;
ra=e,rb=f;
}
return MP(ra,rb);
}
ll n,r;
int main(){
scanf("%lld",&T);
U.y=1;R.sum=1;
for(int Case=1;Case<=T;Case++){
cin>>n>>r;
pair<ll,ll> qr=sbt(r);
// cout<<qr.first<<"/"<<qr.second<<endl;
node res=calc(qr.first,qr.second,0,n,U,R);
printf("%lld\n",res.sum);
}
return 0;
}
- PE372 光锥
参考了 beginendzrq 的题解,_ANIG_ 的提示,Qcfff 写的代码。我抄抄抄抄抄抄
给定 \(m,n\),求:
保证 \(\dfrac{n}{m}\le 500\)。
我们枚举 \(t=\left\lfloor\dfrac{y^2}{x^2}\right\rfloor\),有:
看一下它的几何含义:
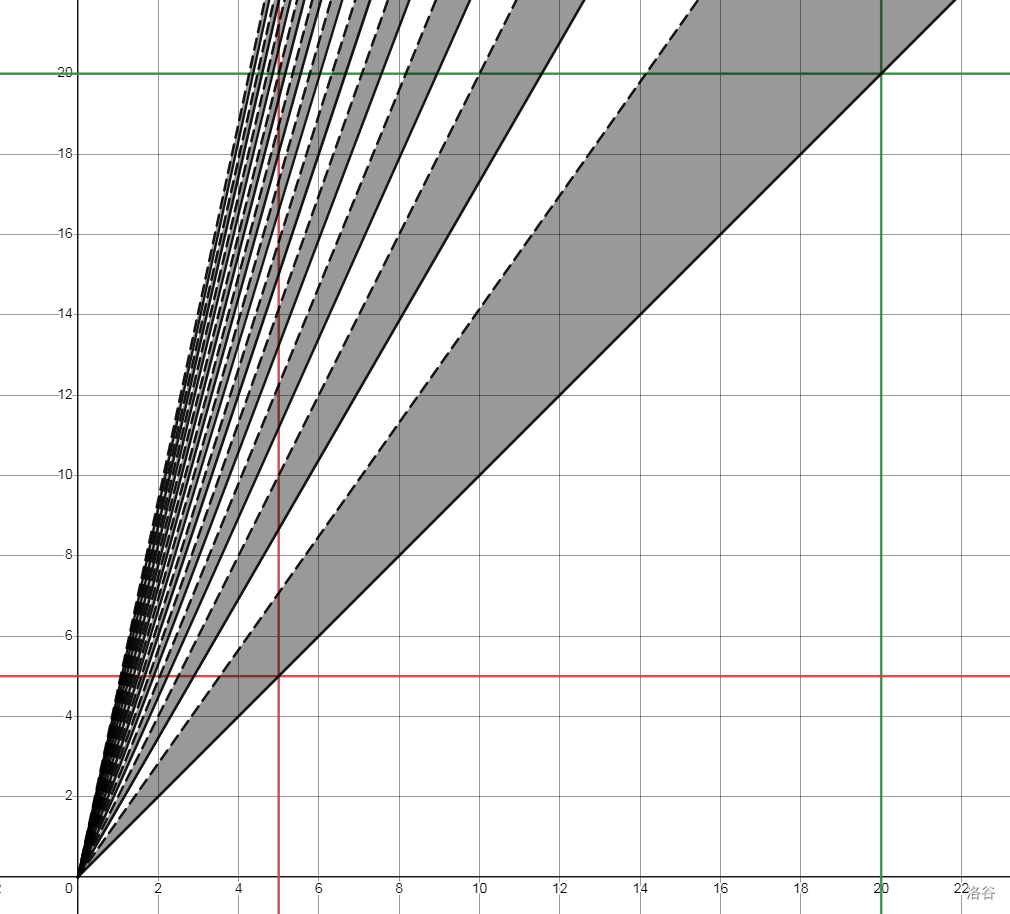
我们要求红绿线围成的正方形里,黑色阴影中的整点数量。
\(t\) 其实是在枚举斜率,每条直线都是一个以 \(\sqrt t\) 为斜率的直线。
我们可以考虑求出每条直线与正方形上边,左边围成的三角形中有多少个点。
以 \(y=\sqrt 2x\) 为例:
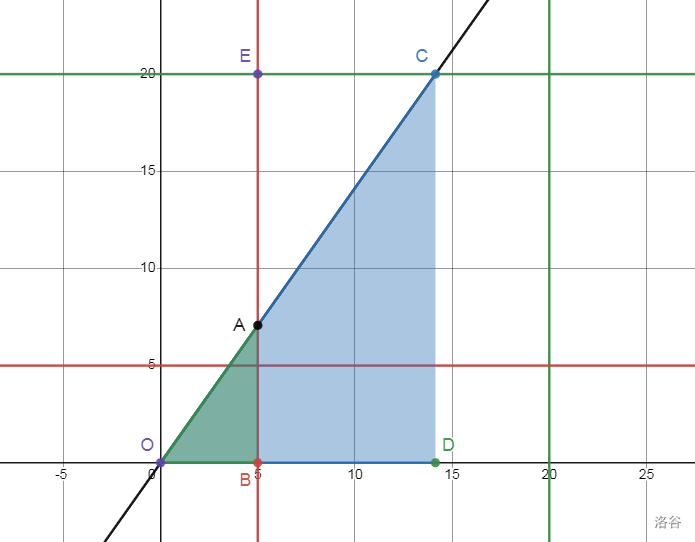
我们分别用万欧求出 \(\triangle OAB\) 中整点个数,记为 \(u\),再求出 \(\triangle OCD\) 内的整点个数,记为 \(v\)。
\(u-v\) 即为蓝色梯形 \(ABCD\) 中整点个数。
我们再用大长方形 \(BECD\) 中的整点个数,减去 \(u-v\),就能得到 \(\triangle AEC\) 中的整点个数。
当然我们需要考虑线段 \(AC\) 上的整点个数。
当 \(t\) 不为平方数,上述做法完全可以。
当 \(t\) 为平方数,我们万欧时会计算 \(AC\) 上的整点,而用长方形一减就减没了。于是我们还需要加上直线上的整点数。
具体看代码:
for(int k=1;k<=lim;k++){
ll now=0;
pair <ll,ll> tmp=sbt(k);
ll l=m,r=(double)n/sqrt((double)k);
now += calc(tmp.first,tmp.second,0,r,U,R).sumy;
now -= calc(tmp.first,tmp.second,0,l,U,R).sumy;
now = (r - l ) * (n) - now;
ll qk=sqrt(k);
if(qk*qk==k){
now += (r-l);
}
if(k%2==1) res += now;
else res -= now;
}printf("%lld\n",res);
r 是点 \(C\) 的横坐标,即解方程 \(\begin{cases}y=\sqrt t x\\y=n\end{cases}\) 得 \(x=\dfrac{n}{\sqrt t}\)。
应该很直观了。我们万欧时套个 SB 树板子,把根号变成分数就能算了。
另外,特别鸣鸣鸣鸣鸣鸣鸣鸣鸣鸣鸣鸣谢 Qcfff 想出的做法和实现的代码,我都是抄他的,他真的我哭死呜呜呜
点击查看代码
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
#define fr(a) freopen(a,"r",stdin)
#define fw(a) freopen(a,"w",stdout)
#define MP(a,b) make_pair(a,b)
#define DEBUG
using namespace std;
typedef long long ll;
const long long N=1e15;
ll m,n;
struct node{
ll x,y,sumy;
node() : x(0) , y(0), sumy(0) {};
node operator *(node b){
node a=*this,c;
c.x=a.x + b.x;
c.y=a.y + b.y;
c.sumy = a.sumy + b.sumy + a.y * b.x;
return c;
}
}U,R,res;
node qpow(node a,ll n){
node res;
while(n){
if(n&1) res = res * a;
a=a*a,n>>=1;
}return res;
}
ll div(ll a,ll b,ll c,ll d){
return ((long double)1.0*a*b+c)/d;
}
node calc(ll p,ll q,ll r,ll n,node U,node R){
if(!n) return node();
if(r >= q) return qpow(U,r/q) * calc(p,q,r%q,n,U,R);
if(p >= q) return calc(p%q,q,r,n,U,qpow(U,p/q) * R);
ll m = div(p,n,r,q);
if(!m) return qpow(R,n);
return qpow(R,(q-r-1)/p) * U * calc(q,p,(q-r-1)%p,m-1,R,U) * qpow(R,n-div(q,m,-r-1,p));
}
pair <ll,ll> sbt(ll x){
ll a=0,b=1,c=1,d=0;
ll ra,rb;
ll tmp=sqrt(x);
if(tmp*tmp==x) return MP(tmp,1);
while(1){
ll e=a+c,f=b+d;
if(f>N) break;
if(e*e < f*f*x) a=e,b=f;
else c=e,d=f;
ra=e,rb=f;
}
return MP(ra,rb);
}
int main(){
scanf("%lld%lld",&m,&n);
ll lim=n*n/(m+1)/(m+1),res=0;
cout<<lim<<endl;
U.y=1,R.x=1;
for(int k=1;k<=lim;k++){
ll now=0;
pair <ll,ll> tmp=sbt(k);
ll l=m,r=(double)n/sqrt((double)k);
now += calc(tmp.first,tmp.second,0,r,U,R).sumy;
now -= calc(tmp.first,tmp.second,0,l,U,R).sumy;
now = (r - l ) * (n) - now;
ll qk=sqrt(k);
if(qk*qk==k){
now += (r-l);
}
if(k%2==1) res += now;
else res -= now;
}printf("%lld\n",res);
return 0;
}


