决策树

一、决策树是一种基本的分类与回归方法。
二、决策树学习的三个步骤：特征选择、生成决策树、决策树修剪

 

三、特征选择：
特征选择的准则是信息增益或信息增益比 
1、信息增益
信息熵定义：

 

熵越大，随机变量的不确定性越大
当随机变量只取两个值，0，1时，X的分布为：

 

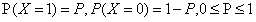
熵为

 

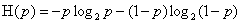
此时，熵H(p)随概率p变化的曲线如下图所示（单位比特）

 

当p=0或p=1时，H(p)=0,随机变量完全没有不确定性，当p=0.5时，H(p)=1，随机变量的不确定性最大
信息增益：g(D,A) = H(D) - H(D|A)

例1：下表是一个由15个样本组成的贷款申请训练数据，数据包括贷款人的4个特征（属性）：第1个特征是年龄，有3个可能值：青年，中年，老年；第2个特征是有工作，有两个可能值：是，否；第3个特征是有自己的房子，有2个可能值：是，否；第4个特征是信贷情况，有3个可能值：非常好，好，一般。表的最后一列是类别，是否同意贷款，取2个值：是，否。

ID	年龄	有工作	有自己的房子	信贷情况	类别
1	青年	否	否	一般	否
2	青年	否	否	好	否
3	青年	是	否	好	是
4	青年	是	是	一般	是
5	青年	否	否	一般	否
6	中年	否	否	一般	否
7	中年	否	否	好	否
8	中年	是	是	好	是
9	中年	否	是	非常好	是
10	中年	否	是	非常好	是
11	老年	否	是	非常好	是
12	老年	否	是	好	是
13	老年	是	否	好	是
14	老年	是	否	非常好	是
15	老年	否	否	一般	否

 

题：对上表拨给的数据集D，根据信息增益准则选择最优特征
首先计算经验熵H(D).

 

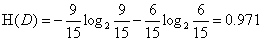
然后计算各特征对数据集D的信息增益，分别以A1,A2,A3,A4表示年龄、有工作、有自己的房子和信贷情况4个特征，则
（1）根据年龄特征计算信息增益

 

 

（2）根据工作特征计算信息增益

 

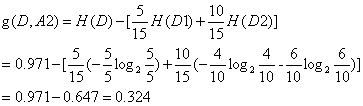
（3）根据有无房特征计算信息增益

 

（4）根据信贷特征计算信息增益

 

 

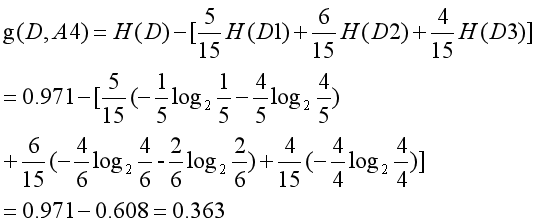
比较各特征的信息增益值，由于特征A3(有自己的房子)的信息增益值最大，所以选择特征A3作为最优特征。

 

 

例2 对上表的训练数据，利用ID3算法建立决策树。

利用上面的结果，由于特征A3(有自己的房子)的信息增益值最大，所以选择特征A3作为根结点的特征。它将训练数据集D划分为两个子集D1(A3取值为“是”)和D2(A3取值为“否”)。由于D1只有一个样本点，所以它成为一个叶结点，结点的类标记为“是”。

对D2则需要从特征A1（年龄），A2(有工作)和A4（信贷情况）中选择新的特征，计算各个特征信息增益：

 

（1）根据年龄特征计算信息增益

 

 

 

 

 

（2）根据工作特征计算信息增益

 

 

 

 

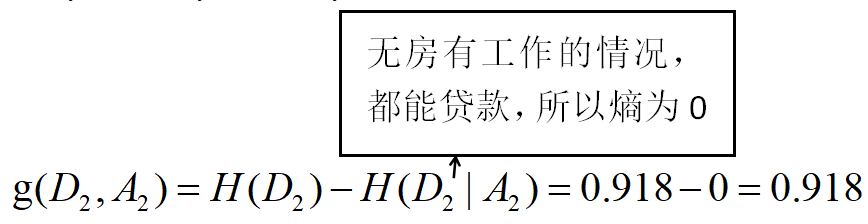
（4）根据信贷特征计算信息增益

 

 

 

信息增益比
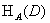特征A对训练数据集D的信息增益比定义为其信息增益g(D,A)与训练数据D关于特征A的值的熵之比，

其中，，n是特征A取值的个数。

 

 

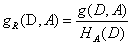
二、衡量数据不纯度指标
(1)、gini系数：值越小，不纯度越低，数据越纯，即数据越倾向于一个类别

 

(2)、Entropy（信息熵）：值越小，不纯度越低，数据越纯，即数据越倾向于一个类别
公式：

 

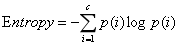
信息熵越低，数据越纯
二、信息增益 = 分叉前不纯度 - 分叉后的不纯度