一、欧氏距离(Euclidean Distance)
1、定义:两点间的直线距离
2、公式:
(1)、二维平面a(x1,y1),b(x2,y2)的欧式距离
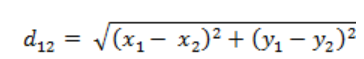
(2)、三维平面a(x1,y1,z1),b(x2,y2,z2)的欧式距离

3、代码实现:
以下python代码都依赖包numpy、math
#Euclidean 欧式距离算法,传入参数为两个点向量,返回值为欧式距离
def Euclidean(vec1,vec2):
npvec1,npvec2 = np.array(vec1),np.array(vec2)
return math.sqrt(((npvec1 - npvec2) ** 2).sum())
二、曼哈顿距离(Manhattan Distance)
1、定义:从曼哈顿的一个十字路口到另一个十字路口,行走距离显然不是两点间的直线距离,这个实际的行走距离即为“曼哈顿距离”,曼哈顿距离又称为“城市街区距离”

2、公式:
(1)、二维平面a(x1,y1),b(x2,y2)的曼哈顿距离

3、代码实现
def Manhattan(vec1,vec2):
npvec1, npvec2 = np.array(vec1), np.array(vec2)
return np.abs(npvec1 - npvec2).sum()
三、切比雪夫距离(Chebyshev Distance)
1、定义:国际象棋中,国王可以直行,横行,斜行,所以国王走一步可以移动到相邻8个格子中任一个,国王从格子(x1,y1)到格子(x2,y2)最少需要多少步,这个距离就叫切比雪夫距离。

2、公式:
二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离

3、代码:
def Chebyshev(vec1,vec2):
npvec1, npvec2 = np.array(vec1), np.array(vec2)
return max(np.abs(npvec1 - npvec2))
四、闵可夫斯基距离(Minkowski Distance)
1、定义:闵氏距离不是一种距离,而是一组距离的定义,是对多个距离度量公式的概括性的表述
2、公式:两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为
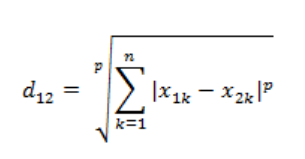
当p=1时,就是曼哈顿距离
当p=2时,就是欧式距离
当p=∞时,就是切比雪夫距离
3、代码:
def Minkowski(vec1,vec2,mode):
npvec1, npvec2 = np.array(vec1), np.array(vec2)
if mode == 1:
return np.abs(npvec1 - npvec2).sum()
elif mode == 2:
return math.sqrt(((npvec1 - npvec2) ** 2).sum())
else:
return max(np.abs(npvec1 - npvec2))
五、马氏距离
1、定义:马氏距离是基于样本分布的一种距离。物理意义就是在规范化的主成分空间中的欧氏距离。所谓规范化主成分空间就是利用主成分分析对一些数据进行主成分分解,再对所有主成分分解作归一化,形成新的坐标轴,由这些坐标轴张成的空间就是主成分空间。

2、公式:
有M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到μ的马氏距离表示为:
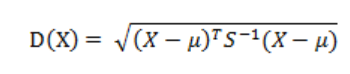
向量Xi与Xj之间的马氏距离定义为:

3、代码:
def Mahalanobis(vec1,vec2):
npvec1, npvec2 = np.array(vec1), np.array(vec2)
npvec = np.array([npvec1,npvec2])
sub = npvec.T[0] - npvec.T[1]
inv_sub = np.linalg.inv(np.cov(npvec1,npvec2))
return math.sqrt(np.dot(inv_sub,sub).dot(sub.T))
六、汉明距离
1、定义:两个等长字符串s1与s2的汉明距离为:将其中一个变为另外一个所需要作的最小字符替换次数
汉明重量:符串中非零的元素个数
2、代码
def Hamming(str1,str2):
i = 0
cnt = 0
while i < len(str1):
if str1[i] != str2[i]:
cnt = cnt + 1
i = i + 1
return cnt




