一、为什么要降维:
1、避免维数灾难,高维情况下容易产生过拟合
2、特征之间如果存在明显的相关性(也叫共线性),此时就需要降维
3、降维可以提取数据中的有效信息,去除噪音数据
4、降维可以降低数据的复杂性,减少模型的训练时间
5、可以方便对数据进行可视化处理,因为维数很高的话,无法可视化
二、PCA降维思想
寻找某个轴线,使得样本映射到该轴线后,能够有最大的可区分度,衡量可区分度的指标就是求方差,现在的问题是如何求得这个轴线,使方差最大。
用方差来定义样本间的间距,方差越大表示数据越稀松,方差越小则表示数据分布越密集,下图即方差公式。
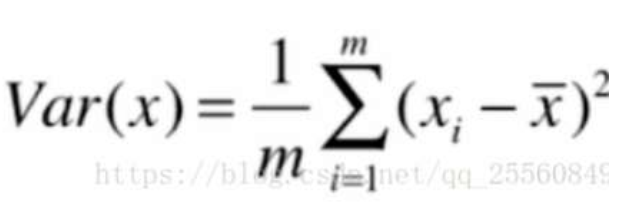
在求解最大方差前,为方便计算,可先对数据进行去均值处理。

去均值后,求最大方差公式可以减少计算的复杂度。
求满足最大方差的轴线可用梯度上升法求解。
PCA和LDA都是降维算法,他们的主要区别是:
PCA为无监督方法,主要是主成分分析方法,Principal Component Analysis, 简称PCA。
PCA可以降到任意维度。
LDA是有监督方法,主要是线性判别分析法,Linear Discriminant Analysis ,简称LDA。
LDA最多只能降到数据类别 -1



