Topological Entropy and Chaos
Topological Entropy and Li-Yorke Chaos
"Topological entropy of maps on the real line"
Let
on
A subset
We summarize some properties of the topological entropy below.
Theorem 1. Let
(a) Let
(a1) If the map
(a2) If the map
(a3) If the map
(b) Suppose that
(c) For any integer
(d) Let
(e) If
(f) Let
(g) If
(h) Let
(i) If
(j)
A dynamical system (X,f) is called minimal if X does not contain any non-empty, proper, closed $f$-invariant subset.
In such a case we also say that the map f itself is minimal.
The following conditions are equivalent:
-$(X,f)$ is minimal,
-every orbit is dense in $X$,
-$\omega_f(x)=X$ for every $x\in X$.
Definition of topological entropy on matric space
For continuous maps on a metric space
By Theorem 1(i) we have
where
Explanation/interpretation (3):
Any compact strictly
Conversely, any
Therefore,
i.e., (3) holds.
Remark.
由上述定义, 为了计算
- 找集合
- 再对每一个
- 最后取它们的上确界得到ent(
值得注意的是:如果我们认为
方,
We start by studying some properties of the new definition of topological entropy, which is summed up in the next result.
Theorem 2 Let
(a) Let
(a1) If the map
(a2) If the map
(a3) If the map
(b) ent(
(c) Let
(d) Let
(e) Let
(f) The conclusion that if
(g) Let
(h) Let
(i) Let
(j) ent(
Proof.
(a)
Since
(a1) If
(a2)
If
(a3) It is immediate consequence of (a1) and (a2).
(b)
We prove ent(
On the other hand, for any
Hence,
and
(c)
We prove that if
By a symmetrical reasoning, we prove that ent(
(d)
We prove that if
Let
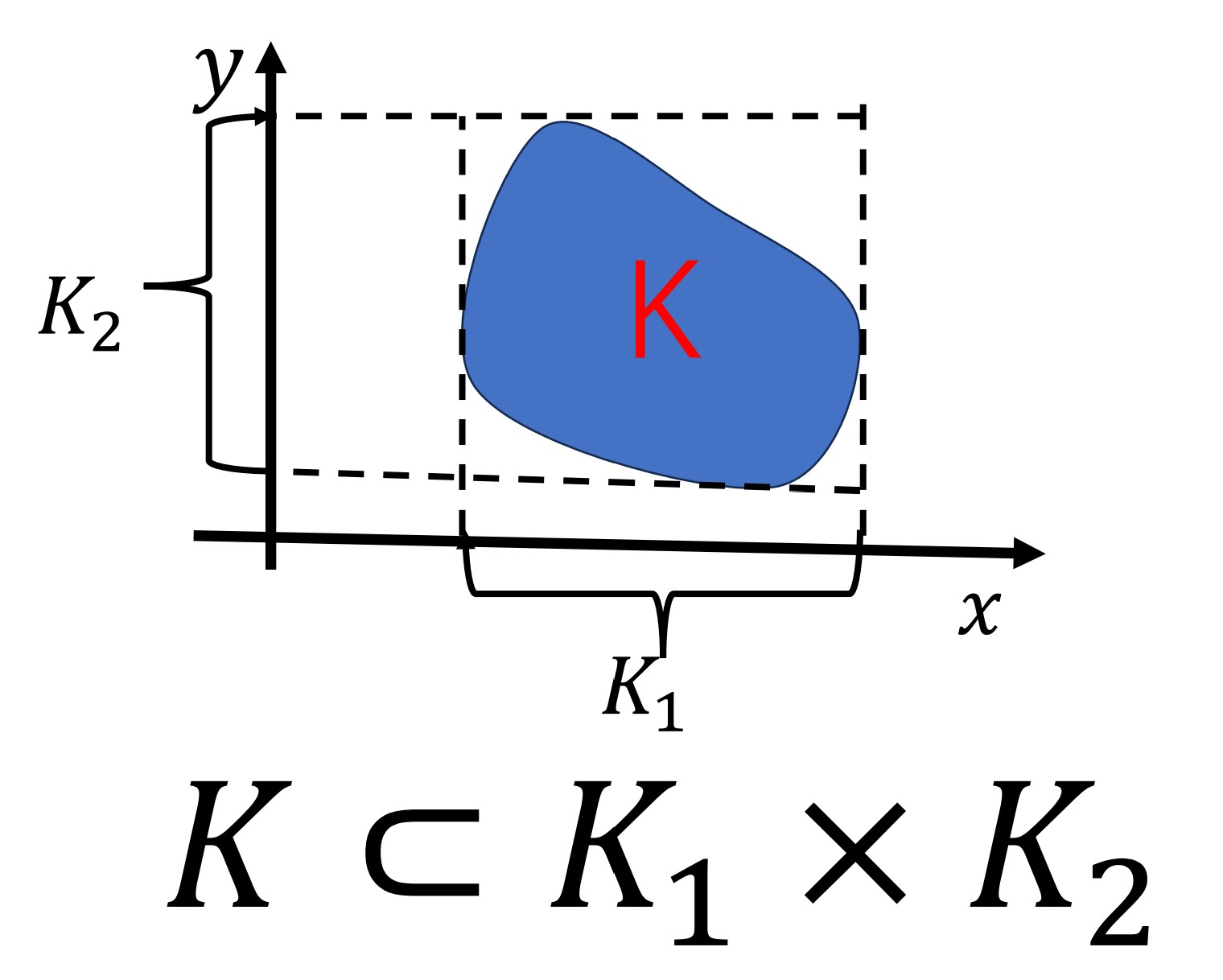
For
Therefore,
and
On the other hand, let
and
By Th1(a2)
Then
(e)
We prove that if
Thus
(f)
We prove that the conclusion that if
(
Let
For example:

Let
It is clear that both sets are invariant by
Therefore, ent(
(g)
Let
compact in
(h)
We prove that if
Since
(i)
We prove that if let
For any
(j)
We prove that
where
there exist positive integer
satisfy the exchange diagram
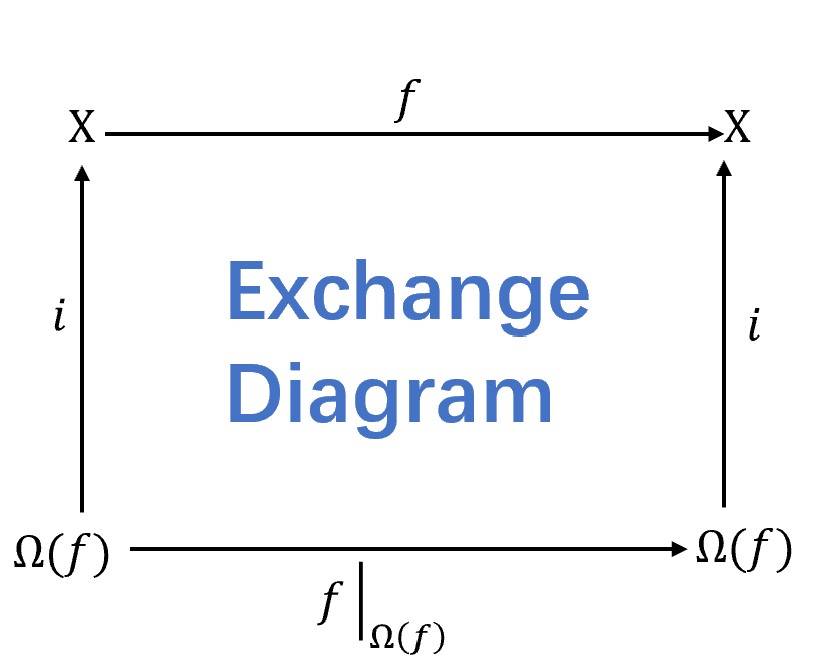
Since
We prove the converse inequality. For any
So
Moreover,
参考文献:
R.L. Adler, A.G. Konheim, M.H. McAndrew, Topological entropy, *Trans. Amer. Math. Soc.* **114** (1965) 309–319.
- R. Bowen, Entropy for group endomorphism and homogeneous spaces, *Trans. Amer. Math. Soc.* **153** (1971) 401–414.
- J. S. Cánovas, J. M. Rodríguez, Topological entropy of maps on the real line, *Topology Appl.*, **153**(2005), 735--746.
- T-Y. Li, J. A. Yorke, Period three implies chaos, *Amer. Math. Monthly*, **82**(1975), 985--992.
- J. Milnor, W. Thurston, On iterated maps of the interval, *Dynamical Systems*, Lecture Notes in Mathematics, vol. **1342**, ed. A. Dold and B. Eckmann, Springer, Berlin, 1988: 465--563.
- M. Rees, A minimal positive entropy homeomorphism of the 2-torus, *J. London Math. Soc.*, **23** (1981) 537–550.
(https://londmathsoc.onlinelibrary.wiley.com/doi/epdf/10.1112/jlms/s2-23.3.537)
- X. Ye, D-function of a minimal set and an extension of Sharkovskiĭ's theorem to minimal sets, *Ergodic Theory Dynam. Systems,* **12**(1992), 365-376.
(https://www.cambridge.org/core/services/aop-cambridge-core/content/view/7737952BD34F742FC1118C8353DB3CE0/S0143385700006817a.pdf/d-function-of-a-minimal-set-and-an-extension-of-sharkovskiis-theorem-to-minimal-sets.pdf)
- http://www.scholarpedia.org/article/Minimal_dynamical_systems#Minimality_of_a_map_and_its_iterates (minimal system)



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 一个费力不讨好的项目,让我损失了近一半的绩效!
· 清华大学推出第四讲使用 DeepSeek + DeepResearch 让科研像聊天一样简单!
· 实操Deepseek接入个人知识库
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库