微分
继续上一节的内容http://www.cnblogs.com/baochuan/p/9047309.html，谈微分。
微分的核心理念就是将函数化繁为简，如把二次的函数简化为一次的函数。
首先，让我们看看几个有意思的case。
减肥
通过对一个人近几个月体重进行线性回归，得到如下图的曲线函数：
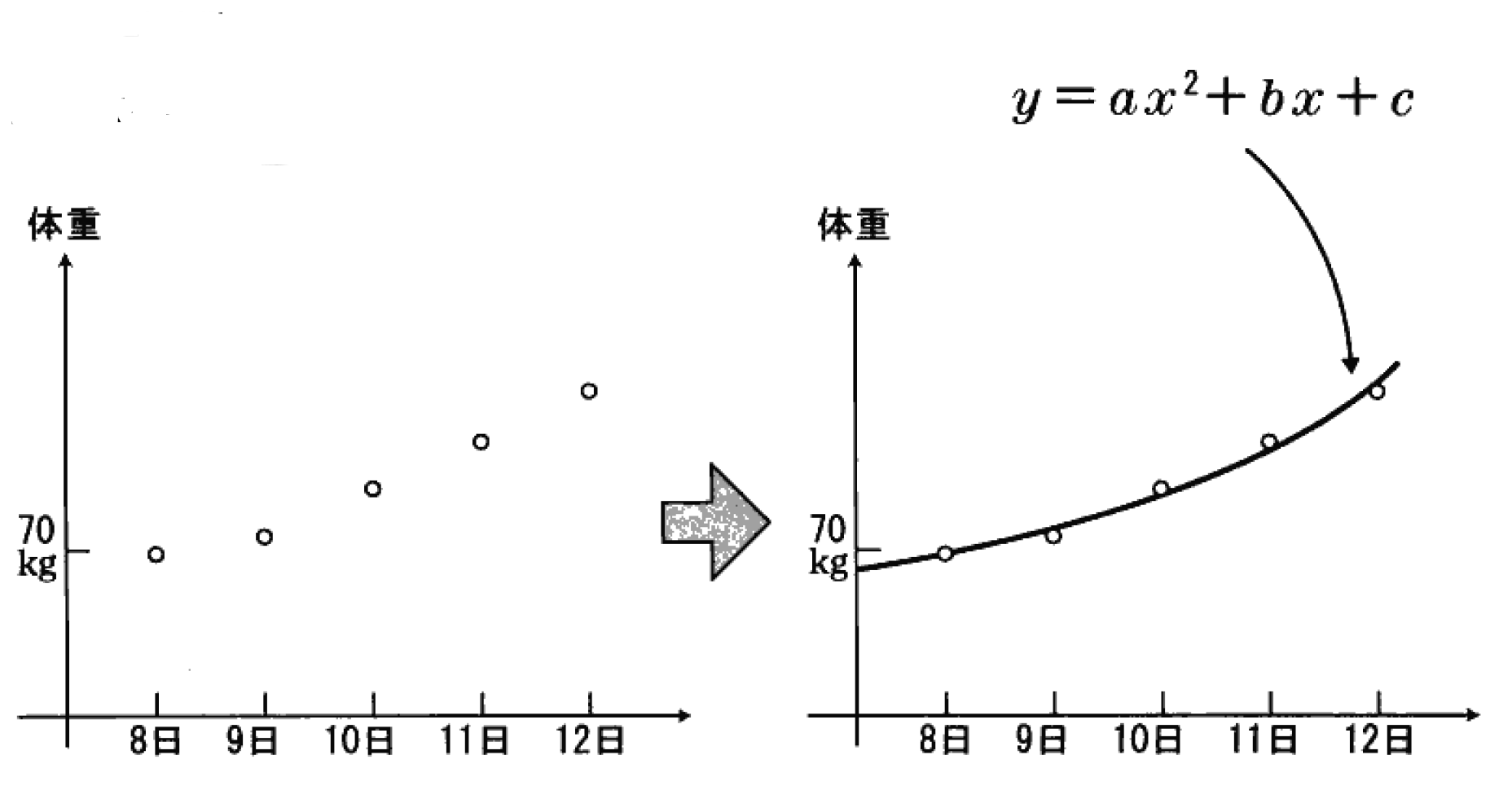
通过对a的设定，我们很容得出如下的结论：
当 a < 0(如：饮食控制、运动)的时候，体重会处于下降趋势，c我们暂定为当前这个人的初始体重。
当 a > 0(如：好吃懒做，毕竟摄入大于消耗吗）的时候，体重会处于上升趋势!
弯曲的道路
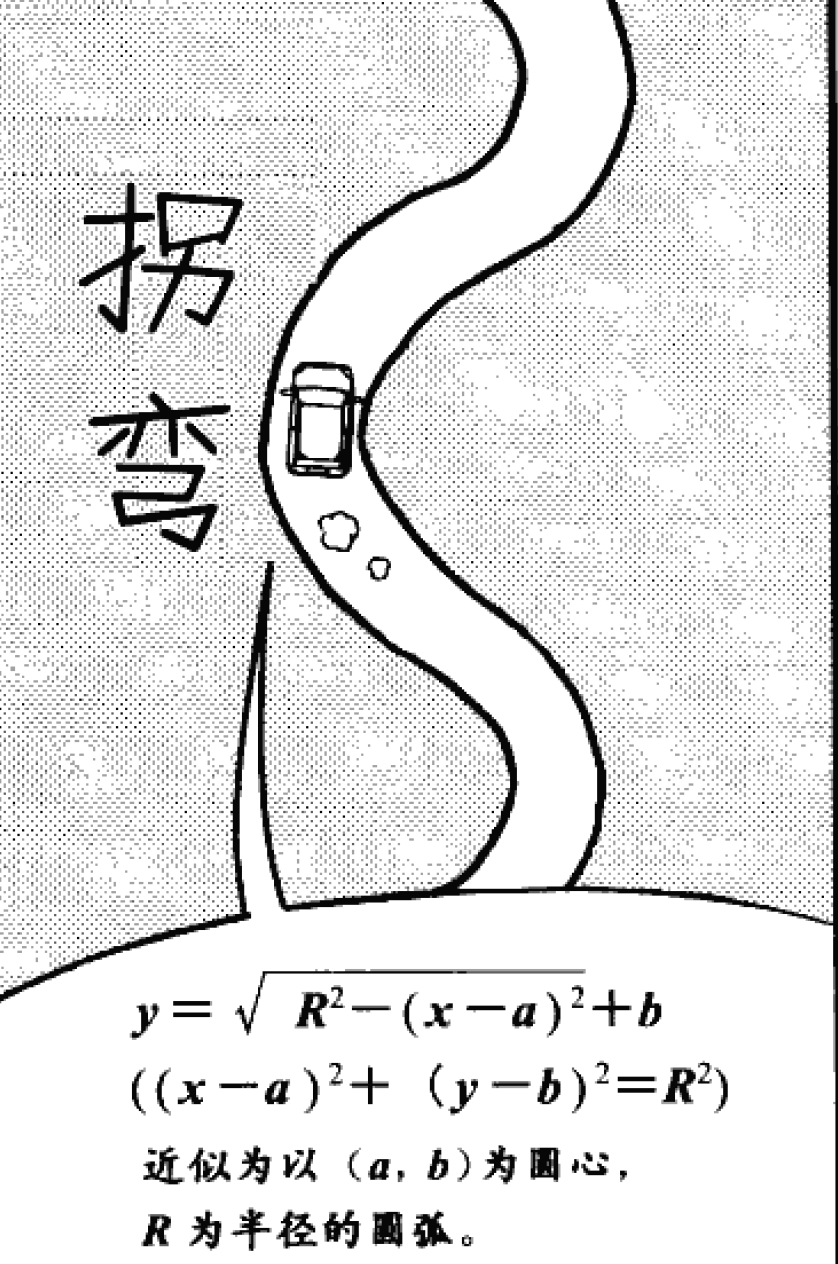
路上弯曲的地方都可以暂时看成半径为R的圆弧。我们可以发现半径越小，弯的越厉害。
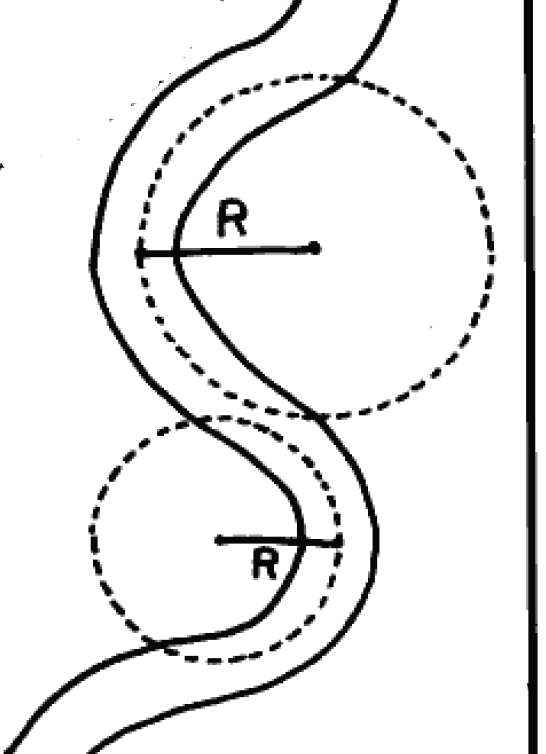
好了，说了这么多，那要说明什么呢？——函数在生活中随处可见。
现在让我们看看怎么做微分的。
说之前，接着举例：
比如，我现在在P点，坐标点为(2,4)，现在要去一家“意大利餐厅”吃饭。假设去的路程是弯曲的，上面说过，弯曲的路程我们可以看成圆弧。大概长这样。
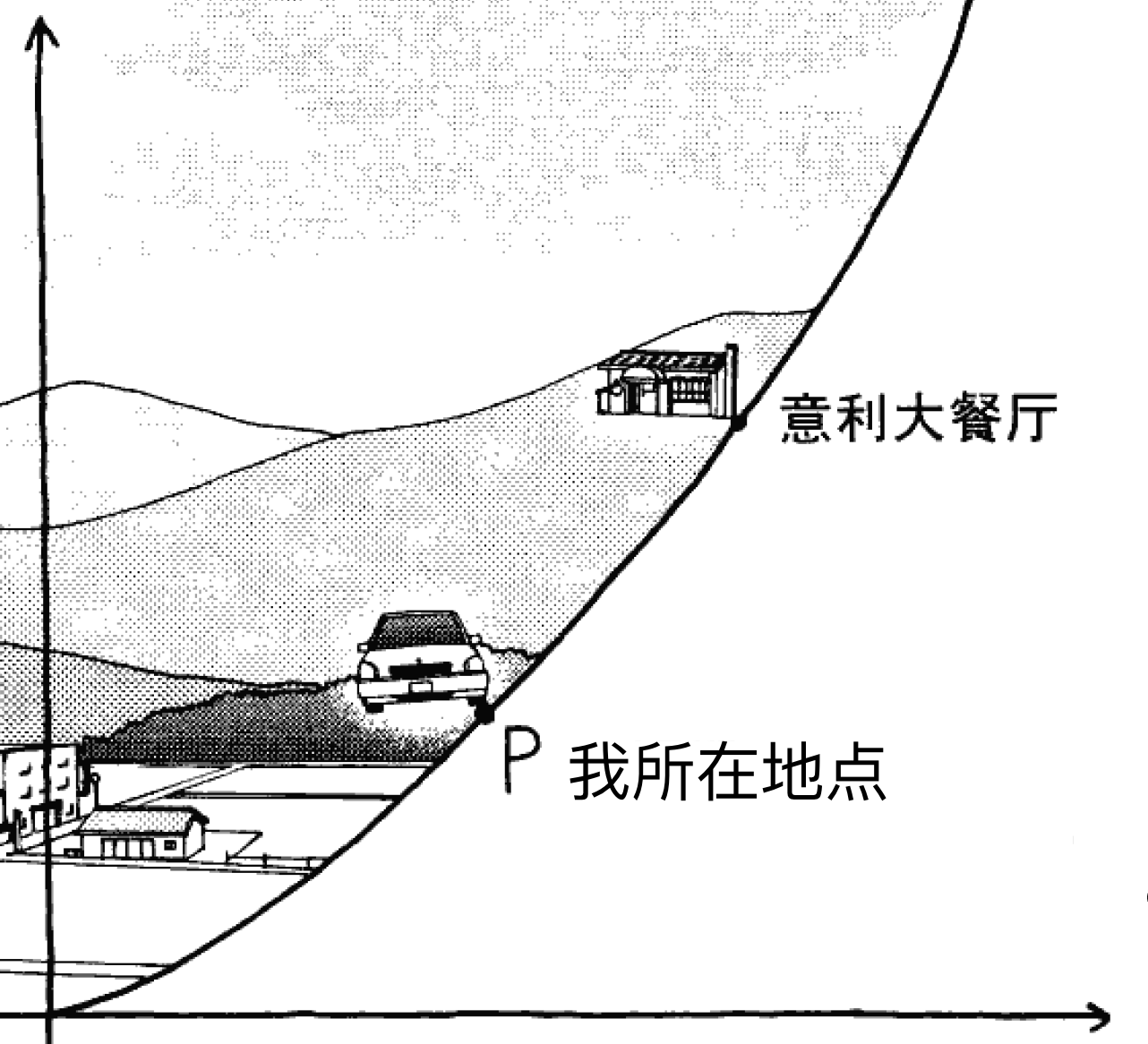
现在我要微分了哈！（化繁为简，把二次的曲线转成一次的直线）
来用一把大刀切出一条路出来！
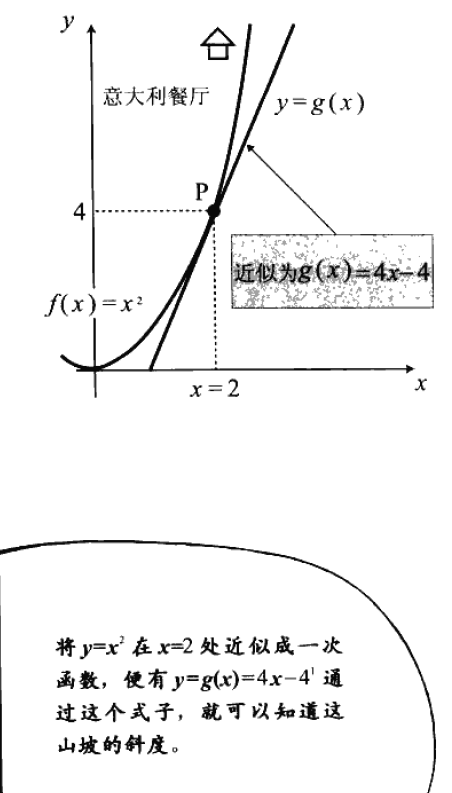
解释下:
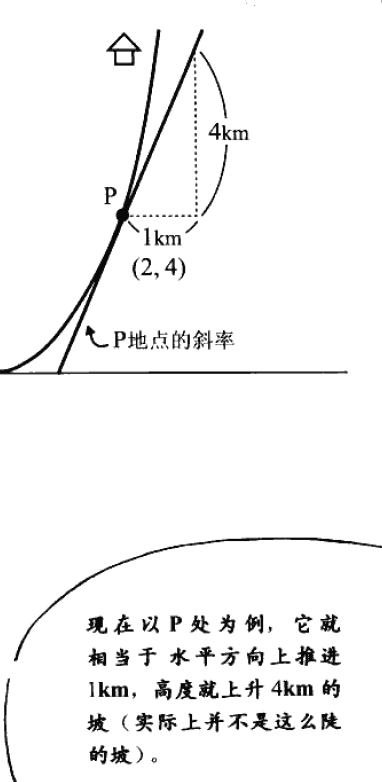
误差率
像上面那么切之后的直线 y=g(x)，跟原来曲线f(x)=x^2相比，毕竟是简化版的，肯定会有一定的误差，我们在实际使用中，我们得有一个忍耐度指标，这个指标我们使用误差率来衡量。实际操作的时候，在一定范围内，我们可以接受使用微分过的直线y=g(x)来替换曲线函数。
那什么是误差率呢？
最终我们可接受的范围如下：
有点对不住大家，我晚8点多开始写的，出于下班时间和篇幅考虑暂时写到这里，没来得及写微分的推到案例。明天接着来。
推荐
喜欢编程
