多线程算法

 

概述

 　

 概念解析：

　　串行算法：在任一时刻仅有一条指令被执行。

　　并行算法：能够在多处理器计算机上运行，并且允许多条指令同时执行。

　　并行计算机：拥有多个处理单元的计算机。并行计算机体系结构模型有多重：如共享存储（每个处理器可都可以直接访问存储器的任何位置），分布式存储（每个处理器的存储器是私有的，处理器之间的访问，通过发送显式消息）。——目前正在向共享存储的并行计算机体系结构模型发展。

　　静态线程：

　　　　应用场景：共享存储并行计算机编程。

　　　　机制：

　　　　　　1） 提供了一个“虚拟处理器”的软件抽象（即线程）。这些线程共享一个相同的存储器。——每个线程维护一个关联的程序计数器，并能与其他线程相互独立地执行代码。

　　　　　　2） 操作系统加载一个线程到处理器上执行，并且在其他的线程需要运行时再把它交换出来。

 

特别地，探讨动态多线程算法的完美模型，它适合算法的设计和分析，并且能再实际应用中有效实现。

 

　　动态多线程：是一类重要的并发平台。程序员只需描述应用中的并行性，这种并发平台包含一个调度器，能自动地进行负载平衡计算，大大减轻了程序员的负担。

　　　　特征：嵌套并行、并行循环。

　　　　 

动态多线程模型

 　 

重点关注：工作量、持续时间和并行度的度量标准，这些将用于分析多线程算法。

 

 case：斐波那契数列

　　　　　　1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144，...

　　　　　　线性递推数列

 单位阶跃函数如下：

 

代码1：

int FIB(n){

　　if n <= 1

　　　　return 1;
　　else

　　　　return FIB(n - 1) + FIB(n - 2);
}

 

问题剖析： 

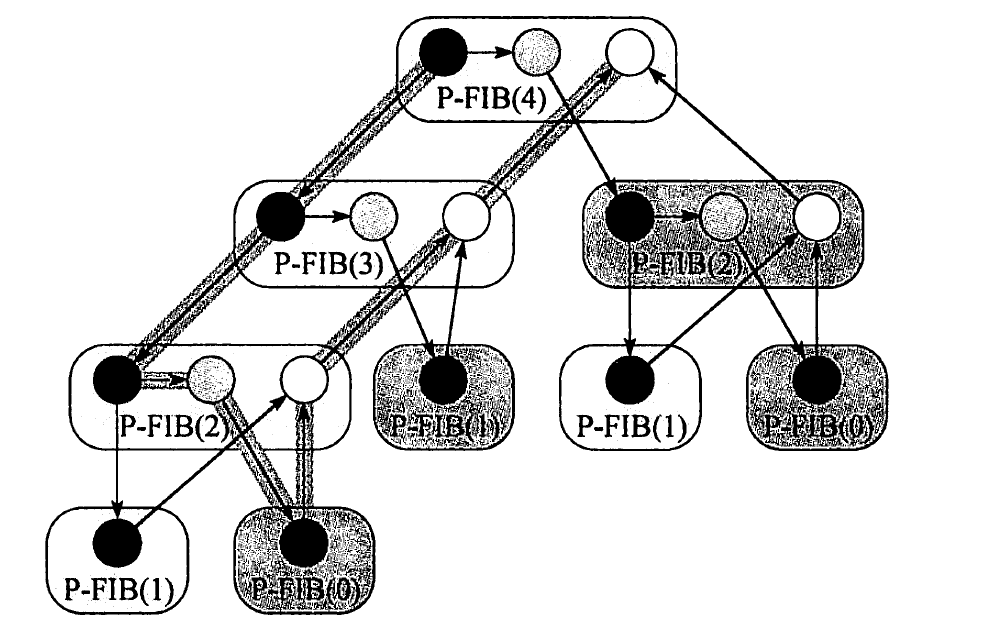
　　当n > 1, 比如2的时候， FIB(0) 会被调用两次。如果是更大的值，必然会出现一个结果重复调用的工作。如下图：

 

 

时间复杂度为：T(n) = Θ(Ø^n)，是以的指数增长，这个过程用来计算斐波那契数列是个相当慢的方法。——得出结论：低效的方法。

 

 代码2（升级版）：采用动态多线程来重写FIB过程，利用代码1中FIB(n-1)和FIB(n-2)彼此独立的特点，可以采用并行计算的方式升级过程。

 

int P-FIB(n)
    if n <= 1
        return n;
    else
        int x = spawn P-FIB(n - 1)
        int y = P-FIB(n - 2)
        sync
        return x + y

 

 关键字spawn的作用：嵌套并行调用。父进程派生子进程，与P-FIB(n - 2)并行执行。

 关键字sync作用：同步语句。执行完sync之后，一个过程（父进程）才能安全地使用其派生子过程（子进程）的返回值。sync表明，过程在执行sync后面的语句前，必须等到它的所有派生子过程计算完成。

 

分析：

时间复杂度由代码1的 T(n) = T(n-1) + T(n-2) 升级为T(n) = max(T(n-1), T(n-2)) ;

 

这里我们要理解一个重要的图分析：有向无环图

 公式：G=（V，E)

 ——V，代表定点（指令）；

 ——Ε ，代表边（指令间的依赖关系）；

　　----如：(μ, ν) ∈  Ε 表示指令 μ必须在 ν之前执行。

 

 

多线程进行矩阵相乘

 　 

 

 

　　　 

多线程归并排序

 　 

    

    

推荐