算法设计与应用作业
CCNU算法设计作业,仅供参考0.0
自己动手,丰衣足食QAQ更新全看心情
Task-1
1.输入一个自然数(<90000), 分别用递归法和非递归法求其二进制表示.
# -*- coding: utf-8 -*-
# @Time : 2019/10/10 21:29
# @Author : BaoBao
# @Mail : baobaotql@163.com
# @File : binary.py
# @Software: PyCharm
#recursion
def recursion(n):
result = ''
if n == 0:
return result
else:
result = recursion(n//2)
return result + str(n%2)
num_a = int(input("input a decimal number : "))
if num_a >= 90000:
print("error!")
else:
print(recursion(num_a))
#non-recursion
def non_recursion(n):
s = ''
while n > 0:
s = str(n%2) + s # 取余后更新 s
n = n//2 # 取整后更新 n
return s
num_b = int(input("input another decimal number : "))
if num_b >= 90000:
print("error!")
else:
print(non_recursion(num_b))
运行截图:
考虑边界情况

随机数情况

2. 分别用递归法和非递归法求Fibonacci数列的前1000位,并比较计算时间的差异.
# -*- coding: utf-8 -*-
# @Time : 2019/10/11 0:25
# @Author : BaoBao
# @Mail : baobaotql@163.com
# @File : Fibonacci.py
# @Software: PyCharm
import time
#recursion
def fib_recursion(n):
if n == 1:
return 1
elif n == 2:
return 1
else:
return fib_recursion(n-1) + fib_recursion(n-2)
num_a = int(input("input a number : "))
tic = time.process_time()
if num_a==0:
print("error!")
else:
print(fib_recursion(num_a))
toc = time.process_time()
print("time : "+ str(1000*(toc-tic)))
#non_recursion
def fib_loop(n):
a = 0
b = 1
c = 0
for i in range(n):
c = a + b
a = b
b = c
return a
num_b = int(input("input a number : "))
tic = time.process_time()
if num_b==0:
print("error!")
else:
print(fib_loop(num_b))
toc = time.process_time()
print("time : " + str(1000 * (toc - tic)))
#another method
class Fibonacci(object):
'''
斐波那契数列迭代器
'''
def __init__(self,n):
'''
:param n: int 指的是生成数列的个数
'''
self.n = n
#保存当前生成的数列的第几个数据 生成器中性质,记录位置,下一个位置的数据
self.current = 0
self.a = 0
self.b = 1
def __next__(self):
'''
:return:当前使用next()函数调用时,就会获取下一个数
'''
if self.current<self.n:
self.a,self.b = self.b,self.a+self.b
self.current +=1
return self.a
else:
raise StopIteration
def __iter__(self):
'''
:return: 迭代器的__iter__返回自身即可
'''
return self
if __name__ == '__main__':
num_c = int(input("input a number : "))
fib = Fibonacci(num_c)
for n in fib:
print(n)
运行截图:
![]()
![]()
![]()
![]()
当计算第1000个数的时候会报错,超过最大递归深度。但是经过其他随机测试可得codes并无错误,但是该怎么解决还在思考中。尝试进行第999个数的计算可行,计算时间超长。
利用datatime模块可以计算并比较递归与非递归的时间差异。
e.g. input a number:35 //已经时间放大1000倍便于观察比较。
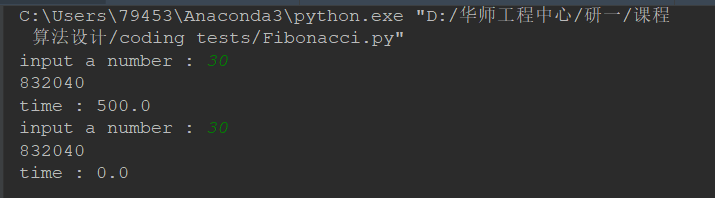
/*后记*/老师要求只求出第50个斐波那契数即可,其实50层迭代的斐波那契数的计算也需要非常多的时间。以30层斐波那契数的计算时间为5s为基础。第50个斐波那契数的计算时间是第30个数的计算的1048,576倍。i7-7700HQ大概需要计算145小时。(当然可能是我计算失误,不是这个时间)

3.用递归算法完成如下问题:有52张牌,使它们全部正面朝上,第一轮是从第2张开始,凡是2的倍数位置上的牌翻成正面朝下;第二轮从第3张牌开始,
凡是3的倍数位置上的牌,正面朝上的翻成正面朝下,正面朝下的翻成正面朝上;第三轮从第4张牌开始,凡是4的倍数位置上的牌按上面相同规则翻转,
以此类推,直到第一张要翻的牌超过52为止。统计最后有几张牌正面朝上,以及它们的位置号.
# -*- coding: utf-8 -*-
# @Time : 2019/10/11 18:42
# @Author : BaoBao
# @Mail : baobaotql@163.com
# @File : card.py
# @Software: PyCharm
#non_recursion
s = [0]*52
print("initial state : ",s,"\n")
for i in range(1,52):
for j in range(i,52):
if((j+1)%(i+1)==0):
if(s[j]==0):
s[j]=1
else:
s[j]=0
print("ending state : ",s,"\n")
vec = [x+1 for x in range(52) if s[x]==0]
print("index : ",vec,"\n")
#recursion
s = [0]*52
print("initial state : ",s,"\n")
def turn_card(n):
if(n>52):
return
else:
for j in range(n,52):
if ((j + 1) % (n + 1) == 0):
if (s[j] == 0):
s[j] = 1
else:
s[j] = 0
turn_card(n+1)
turn_card(1)
print("ending state : ", s, "\n")
vec = [x+1 for x in range(52) if s[x]==0]
print("index : ",vec,"\n")
运行截图:

4.一个射击运动员打靶,靶一共有10环,连开6枪打中45环的可能性有多少种? (每一枪最少是0环,最多是10环)
# -*- coding: utf-8 -*-
# @Time : 2019/10/12 11:29
# @Author : BaoBao
# @Mail : baobaotql@163.com
# @File : shooting.py
# @Software: PyCharm
times = 0
def shooting(n,sum):
global times
if n<0:
return
elif (45 - sum)>(10*(n)):
return
elif (sum == 45) and (n == 0):
times += 1
return
for i in range(11):
shooting(n - 1,sum + i)
shooting(6,0)
print('there are %d possibilities'%times)
运行截图:

5.在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,输出所有摆法。
# -*- coding: utf-8 -*- # @Time : 2019/10/12 17:00 # @Author : BaoBao # @Mail : baobaotql@163.com # @File : queens.py # @Software: PyCharm def is_rule(queen_tup, new_queen): """ :param queen_tup: 棋子队列,用于保存已经放置好的棋子,数值代表相应棋子列号 :param new_queen: 被检测棋子,数值代表列号 :return: True表示符合规则,False表示不符合规则 """ num = len(queen_tup) for index, queen in enumerate(queen_tup): if new_queen == queen: # 判断列号是否相等 return False if abs(new_queen - queen) == num - index: # 判断列号之差绝对值是否与行号之差相等 return False return True def arrange_queen(num, queen_tup=list()): """ :param num:棋盘的的行数,当然数值也等于棋盘的列数 :param queen_tup: 设置一个空队列,用于保存符合规则的棋子的信息 """ for new_queen in range(num): # 遍历一行棋子的每一列 if is_rule(queen_tup, new_queen): # 判断是否冲突 if len(queen_tup) == num - 1: # 判断是否是最后一行 yield [new_queen] # yield关键字 else: # 若果不是最后一行,递归函数接着放置棋子 for result in arrange_queen(num, queen_tup + [new_queen]): yield [new_queen] + result for i in arrange_queen(8): print(i)
运行截图(部分):

Task-2
迷宫问题:设有8*8的方格迷宫,入口和出口分别在左上角和右上角,迷宫格子中分别有0和1,1代表不能走,
迷宫走的规则如图。当迷宫给出后,找到一条从入口到出口的通路。

源代码:
-*- coding: utf-8 -*- # @Time : 2019/10/19 10:26 # @Author : BaoBao # @Mail : baobaotql@163.com # @File : mzae.py # @Software: PyCharm import numpy as np maze =np.array ([ [0, 0, 0, 0, 0, 0, 1, 0], [1, 0, 1, 1, 1, 1, 1, 0], [0, 1, 0, 0, 1, 0, 0, 1], [0, 0, 1, 1, 0, 1, 0, 1], [0, 1, 0, 0, 0, 1, 1, 0], [0, 1, 1, 1, 1, 1, 0, 1], [0, 0, 1, 1, 1, 0, 1, 1], [1, 1, 0, 0, 1, 0, 0, 0], ]) p = np.array([1, 1, 1, 1, 1, 1, 1, 1]) q = np.array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1]) a = np.insert(maze, 0, values=p, axis=1) b = np.insert(a, 9,values=p, axis=1) c = np.insert(b, 0, values=q, axis=0) d = np.insert(c, 9, values=q, axis=0) print("初始化迷宫:") print(d)#为解决越界问题 初始化迷宫 dirs = [lambda x, y: (x + 1, y), lambda x, y: (x - 1, y), lambda x, y: (x, y - 1), lambda x, y: (x, y + 1), lambda x, y: (x + 1, y - 1), lambda x, y: (x + 1, y + 1), lambda x, y: (x - 1, y - 1), lambda x, y: (x - 1, y + 1) ] def mpath(x1, y1, x2, y2): stack = [] #建立抽象栈 stack.append((x1, y1)) #加入初始点 d[x1][y1] = -1 #表示已经走过 while len(stack) > 0: curNode = stack[-1] if curNode == (x2, y2): print(stack) return True for dir in dirs: nextNode = dir(curNode[0], curNode[1]) if d[nextNode[0]][nextNode[1]] == 0 : #找到了下一个 stack.append(nextNode) d[nextNode[0]][nextNode[1]] = -1 # 标记为已经走过,防止死循环 break else: #八个方向都没找到 d[curNode[0]][curNode[1]] = -1 # 死路一条,标记下次不走 stack.pop() #回溯 print("没有路") return False mpath(1,1,8,8)
运行截图:

Task-3
1.利用动态规划算法求解编辑距离问题,给定两个字符串,求由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符
# -*- coding: utf-8 -*- # @Time : 2019/12/1 17:25 # @Author : BaoBao # @Mail : baobaotql@163.com # @File : Edit_Distance.py # @Software: PyCharm ''' 利用动态规划算法求解编辑距离问题 ''' def minDistance(word1, word2): ''' :param word1: 传入字符串word1 :param word2: 传入字符串Word2 :return: 返回距离矩阵元素 ''' m = len(word1) n = len(word2) if m == 0: return n if n == 0: return m dp = [[0] * (n+1) for _ in range(m+1)] #初始化表格[m+1, n+1] # 计算边界 for i in range(1, m+1): dp[i][0] = i for j in range(1, n+1): dp[0][j] = j for i in range(1, m+1): #计算dp for j in range(1, n+1): if word1[i-1] == word2[j-1]: dp[i][j] = dp[i-1][j-1] else: dp[i][j] = min(dp[i-1][j-1]+1, dp[i][j-1]+1, dp[i-1][j]+1) return dp[m][n] if __name__ == "__main__": dis = minDistance('www.ccnu.edu.cn', 'www.neu.edu.cn') print("The longest Edit Distance is :", dis)
运行截图
2.用动态规划算法求最长公共子序列问题.
# -*- coding: utf-8 -*- # @Time : 2019/12/1 17:32 # @Author : BaoBao # @Mail : baobaotql@163.com # @File : LCS.py # @Software: PyCharm import numpy as np def Longest_Common_Subsequence(a, b): ''' :param a:字符串a :param b:字符串b :return:length subseq ''' length = 0 subseq = '' cell = np.zeros(shape=(len(a), len(b))) for i in range(len(a)): for j in range(len(b)): if a[i] == b[j]: cell[i][j] = cell[i - 1][j - 1] + 1 if cell[i][j] > length: length = cell[i][j] subseq += a[i] else: cell[i][j] = max(cell[i-1][j], cell[i][j-1]) return length, subseq if __name__ == "__main__": a, b = Longest_Common_Subsequence('www.ccnu.edu.cn', 'www.neu.edu.cn') print('The length of longest common subsequence is:%d\nThe Longest Common Subsequence is:%s' % (a, b))
运行截图

算法分析在本人github上欢迎交流~~~
对你有帮助就支付宝请我喝可乐叭~~~




