扫描线学习笔记
第一次写qwq小小的记录一下
自己能看懂就行了
介绍
扫描线扫描线，字面意思就是用一根线扫描一下（雾
Oi Wiki上这个图很直观
我们可以根据扫描线被图形截得的线段来求一些东西，比如图形的面积并啦、周长并啦等等。具体看下面的。
面积并
比如我们想求一些矩形覆盖的面积。参考上面的图，我们可以把整块面积分割成那些彩色小矩形来求。也就是 \(\sum\) 截线段长度*相邻两条截线段的高度差。
相邻两条截线段的高度差很好求，那截线段长度怎么办捏
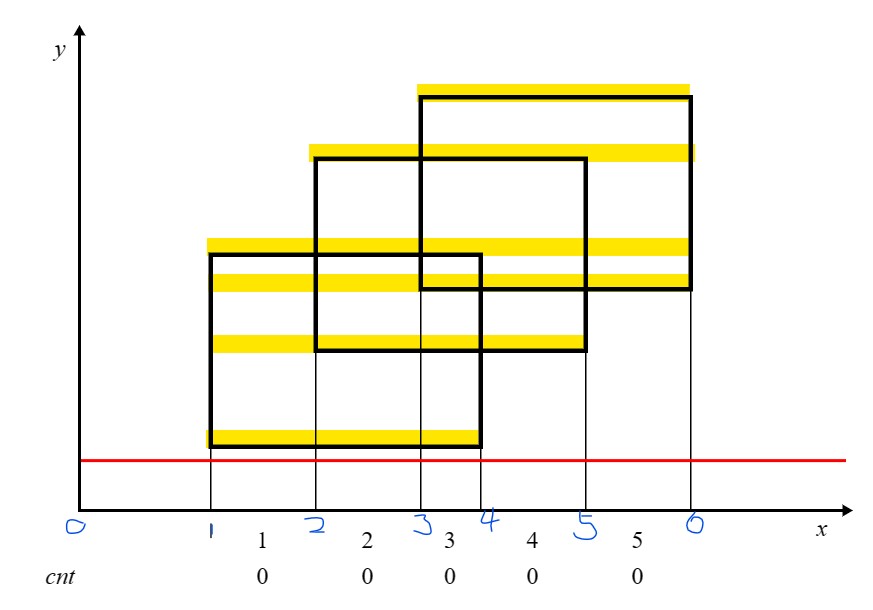
哦这些黄色的就是截线段，看见他想到了什么。
线段覆盖呀
模拟一下：
① 扫描线最先碰到的矩形的边是最下面的 \([1,4]\) ，我们把 \(cnt[1,4]\) 都加上 \(1\) 。这时只有 \([1,4]\) 是被覆盖的，所以第一根截线段长为 \(3\) 。
② 接着碰到了第二个矩形的边 \([2,5]\) ， 我们把 \(cnt[2,5]\) 都加上 \(1\) 。这次 \([1,5]\) 不为空代表被覆盖了，第二根截线段长为 \(4\)
……
④ 这回碰到了第一个矩形上面的边，它下面的边我们最开始已经加过了，所以现在要删掉，将 \(cnt[1,4]\) 都减掉 \(1\) 。现在不为空的仍为 \(1,6\) ，截线段长为 \(5\) 。
好像找到了规律。我们把一个矩形从下面的边叫做入边，扫到它的时候将区间每个数 \(+1\) ，把同一个矩形上面的边叫做出边，扫到它的时候将区间每个数 \(-1\) 。被覆盖的长度就是整个区间不为空的长度辣。
诶区间修改区间查询，我们拿线段树来维护一下就好了。
具体操作下面这个讲的很详细了。我不想打了
P5490 【模板】扫描线
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define lson(x) (x<<1)
#define rson(x) (x<<1|1)
using namespace std;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const int N=1e5+5;
struct Seg_tree{
int l,r,sum,cover;
}tr[8*N];
struct scanline{
int l,r,h,mark;
friend bool operator < (scanline x,scanline y){
return x.h<y.h;
}
}a[2*N];
int x[2*N],cnt;
void pushup(int i){
if(tr[i].l==tr[i].r){
if(tr[i].cover){tr[i].sum=x[tr[i].r+1]-x[tr[i].l];
}else{tr[i].sum=0;}
}else{
if(tr[i].cover){tr[i].sum=x[tr[i].r+1]-x[tr[i].l];
}else{tr[i].sum=tr[lson(i)].sum+tr[rson(i)].sum;}
}
}
void build(int l,int r,int i){
tr[i].l=l,tr[i].r=r;
if(l==r){return;}
int mid=(l+r)>>1;
build(l,mid,lson(i));build(mid+1,r,rson(i));
}
void update(int i,int l,int r,int k){
if(l<=x[tr[i].l]&&x[tr[i].r+1]<=r){tr[i].cover+=k;pushup(i);return;}
if(l<x[tr[lson(i)].r+1]){update(lson(i),l,r,k);}
if(r>x[tr[rson(i)].l]){update(rson(i),l,r,k);}
pushup(i);
}
signed main(){
int n;n=read();
int x1,y1,x2,y2;
for(int i=1;i<=n;i++){
x1=read();y1=read();x2=read();y2=read();
a[++cnt]=(scanline){x1,x2,y1,1};
x[cnt]=x1;
a[++cnt]=(scanline){x1,x2,y2,-1};
x[cnt]=x2;
}
sort(x+1,x+cnt+1);
sort(a+1,a+cnt+1);
int ans=0;
build(1,cnt-1,1);
for(int i=1;i<cnt;i++){
update(1,a[i].l,a[i].r,a[i].mark);
ans+=tr[1].sum*(a[i+1].h-a[i].h);
}
printf("%lld\n",ans);
return 0;
}
周长并
容易想到最简单朴素暴力的方法就是横着扫一遍再竖着扫一遍。
但是我们考虑能不能扫一次就解决横向变和纵向边呢
好哒我们开始从下往上扫，横边的总长就是 \(\sum abs(\) 上次截的线段长 \(-\) 这次截的线段长 \()\) 。理解的话平移法解决。
竖直方向上的长度我们把它看做这些彩色的小棍 显然不包括黄色
然后这些彩色的小棍和什么有关呢 就是看被截的这一行有几个端点，代表有几根小棍，一行的小棍长度是一样的等于相邻两条截线的高度差。
so 竖边总长 \(=\sum\) 端点数 \(*\) 高度。
线段树上维护一个 \(lp,rp\) 表示左右端点的覆盖情况。
P1856 [IOI1998] [USACO5.5] 矩形周长Picture
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define lson(x) (x<<1)
#define rson(x) (x<<1|1)
using namespace std;
const int N=5e3+5;
struct scanline{
int l,r,h,mark;
friend bool operator < (scanline x,scanline y){
return (x.h==y.h)?(x.mark>y.mark):(x.h<y.h);
}
}a[2*N];
struct Seg_tree{
int l,r,sum,num,len,lp,rp;
}tr[8*N];
int cnt,x[2*N];
void build(int l,int r,int i){
tr[i].l=l,tr[i].r=r;
if(l==r){return;}
int mid=(l+r)>>1;
build(l,mid,lson(i));
build(mid+1,r,rson(i));
}
void pushup(int i){
if(tr[i].l==tr[i].r){
if(tr[i].sum){tr[i].lp=tr[i].rp=1;tr[i].num=2;tr[i].len=x[tr[i].r+1]-x[tr[i].l];
}else{tr[i].lp=tr[i].rp=0;tr[i].num=0;tr[i].len=0;}
}else{
if(tr[i].sum){
tr[i].lp=tr[i].rp=1;tr[i].num=2;tr[i].len=x[tr[i].r+1]-x[tr[i].l];
}else{
tr[i].lp=tr[lson(i)].lp;tr[i].rp=tr[rson(i)].rp;
tr[i].len=tr[lson(i)].len+tr[rson(i)].len;
tr[i].num=tr[lson(i)].num+tr[rson(i)].num;
if(tr[lson(i)].rp&&tr[rson(i)].lp)tr[i].num-=2;
}
}
}
void update(int i,int l,int r,int k){
if(l<=x[tr[i].l]&&x[tr[i].r+1]<=r){tr[i].sum+=k;pushup(i);return;}
if(l<x[tr[lson(i)].r+1])update(lson(i),l,r,k);
if(r>x[tr[rson(i)].l])update(rson(i),l,r,k);
pushup(i);
}
signed main(){
int n;scanf("%lld",&n);
int x1,y1,x2,y2;
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2);
a[++cnt]=(scanline){x1,x2,y1,1};x[cnt]=x1;
a[++cnt]=(scanline){x1,x2,y2,-1};x[cnt]=x2;
}
sort(x+1,x+cnt+1);
sort(a+1,a+cnt+1);
int len=unique(x+1,x+cnt+1)-x-1;
build(1,len-1,1);
int ans=0,last=0;
for(int i=1;i<=cnt;i++){
update(1,a[i].l,a[i].r,a[i].mark);
ans+=abs(tr[1].len-last);last=tr[1].len;
ans+=tr[1].num*(a[i+1].h-a[i].h);
}
printf("%lld\n",ans);
return 0;
}
于是乎我们有了第一道紫题
