最佳归并树
无论是通过等分还是置换-选择排序得到的归并段,如何设置它们的归并顺序,可以使得对外存的访问次数降到最低?
1、例如,现有通过置换选择排序算法所得到的 9 个初始归并段,其长度分别为:9,30,12,18,3,17,2,6,24
(1)在对其采用 3-路平衡归并的方式时可能出现如下图所示的情况
(2)叶子结点表示初始归并段,各自包含记录的长度用结点的权重来表示;非终端结点表示归并后的临时文件

(3)假设在进行平衡归并时,操作每个记录都需要单独进行一次对外存的读写,那么归并过程需要对外存进行读或者写的次数为:(9 + 30 + 12 + 18 + 3 + 17 + 2 + 6 + 24) * 2 * 2 = 484(涉及到了两次归并,对外存的读和写各进行 2 次)
(4)从计算结果上看,对于上图中的 3 叉树来讲,其操作外存的次数恰好是树的带权路径长度的 2 倍。所以,对于如何减少访问外存的次数的问题,就等同于考虑如何使 k-路归并所构成的 k 叉树的带权路径长度最短
2、若想使树的带权路径长度最短,就是构造赫夫曼树,对于 k 叉树,只要其带权路径长度最短,亦可以称为赫夫曼树
(1)若对上述 9 个初始归并段构造一棵赫夫曼树作为归并树

(2)其对外存的读写次数为:(2 * 3 + 3 * 3 + 6 * 3 + 9 * 2 + 12 * 2 + 17 * 2 + 18 * 2 + 24 * 2 + 30) * 2 = 446
(3)通过以构建赫夫曼树的方式构建归并树,使其对读写外存的次数降至最低(k-路平衡归并,需要选取合适的 k 值,构建赫夫曼树作为归并树),所以称此归并树为最佳归并树
附加“虚段”的归并树
1、上述图中所构建的为一颗真正的 3叉树(树中各结点的度不是 3 就是 0),而若 9 个初始归并段改为 8 个,在做 3-路平衡归并的时候就需要有一个结点的度为 2
2、对于具体设置哪个结点的度为 2,为了使总的带权路径长度最短,正确的选择方法是:附加一个权值为 0 的结点(称为“虚段”),然后再构建赫夫曼树
(1)例如:若去掉权值为 30 的结点,其附加虚段的最佳归并树如下图所示
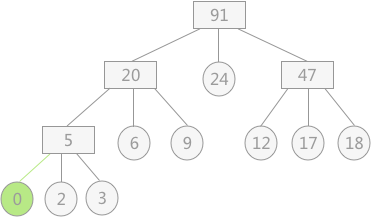
(2)虚段的设置只是为了方便构建赫夫曼树,在构建完成后虚段自动去掉即可
3、对于如何判断是否需要增加虚段,以及增加多少虚段的问题,有以下结论直接套用即可:在一般情况下,对于 k–路平衡归并来说,若 (m - 1) MOD (k - 1) = 0,则不需要增加虚段;否则需附加 k - (m - 1) MOD (k - 1) - 1 个虚段




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战