红黑树
介绍
1.红黑树是平衡二叉排序/搜索树的改进,插入、删除时不需要频繁的旋转
2.红黑树相比平衡二叉排序/搜索树多出了变色操作,且不需要判断左右子树的绝对高度差
与2-3-4树的关系
1、2节点:黑;3节点:上黑下红;4节点:中间黑,左右红
2、红黑树本质是2-3-4树,一个红黑树只对应一个2-3-4树,一个2-3-4树可能对应多个红黑树
3、2-3-4树节点的元素转化为红黑树的节点时,只有一个元素成为黑节点,因此在红黑树的任意节点到该节点的叶子节点路径上黑色节点个数一定是一样的
性质:
1.结点是红色或黑色
2.根是黑色
3.所有叶子节点都是黑色且为NULL结点,叶子结点不能忽略
4.每个结点必须有两个黑色的子结点(从每个叶子到根的所有路径上不能有两个连续的红色结点)
5.从任一结点到其每个叶子的所有简单路径都包含相同数目的黑色结点(黑色平衡)
新增节点
1.插入节点初始为红色
2.插入到空树时,插入节点变为黑色
3.插入节点的父节点为黑色时,直接插入
4.插入节点的父节点和叔节点为红色时,祖父节点必定为黑色,父节点、叔节点变为黑色,祖父节点变为红色;祖父节点按插入节点的情况(1、2、3、4、5)递归处理变色
5.父节点为红色,叔节点为黑色或为null,祖父节点必定为黑色
(1)插入节点、父节点、祖父节点成直线,父节点变为黑色,祖父节点变为红色,旋转祖父节点,使插入节点、祖父节点变成父节点的子节点
(2)插入节点、父节点、祖父节点成三角,旋转父节点,使父节点变成插入节点的子节点,此时插入节点、父节点、祖父节点成直线,按(1)处理
删除节点
1.删除红色节点
(1)红色节点要么两个子树,要么为叶子节点
(2)按照二叉排序树方法删除
2.删除黑色节点
(1)若节点有两棵子树,用其后继节点/前驱节点代替,判断后继节点/前驱节点的颜色,然后删除待删除节点,此节点必定最多只有一棵子树,转跳到步骤2或删除红色/黑色叶子节点
(2)若节点仅有左子树/右子树,子节点必定为红色,用子节点替换待删除节点,并改成黑色
3.删除黑色叶子节点
(1)若兄弟节点为红色,必有两个黑色子节点,父节点必定为黑色,父节点和兄弟节点互换颜色,父节点向待删除节点方向旋转,使待删除节点的兄弟节点变成黑色,转跳到步骤2或步骤3
(2)若兄弟节点为黑色,有一个红色近侄子节点,兄弟节点向近侄子节点的反方向旋转,并交换颜色,使兄弟节点变远侄子节点,近侄子节点变兄弟节点,转跳到步骤3
(3)若兄弟节点为黑色,有一个红色远侄子节点,兄弟节点和父节点互换颜色,远侄子节点变为黑色,父节点向删除节点方向旋转,然后删除待删除节点
(4)若父节点为红色,兄弟节点和兄弟节点的两个子节点(只能为null)都为黑色,父节点改成黑色,兄弟节点改成红色,然后删除待删除节点
(5)若父节点,兄弟节点和兄弟节点的两个子节点(只能为null)都为黑色的情况,兄弟节点改成红色,然后删除待删除节点,以父节点作为起始点再次调整
4.总结:判断类型的时候,先看待删除的节点的颜色,再看兄弟节点的颜色,再看侄子节点的颜色(先看远侄子再看近侄子),最后看父节点的颜色
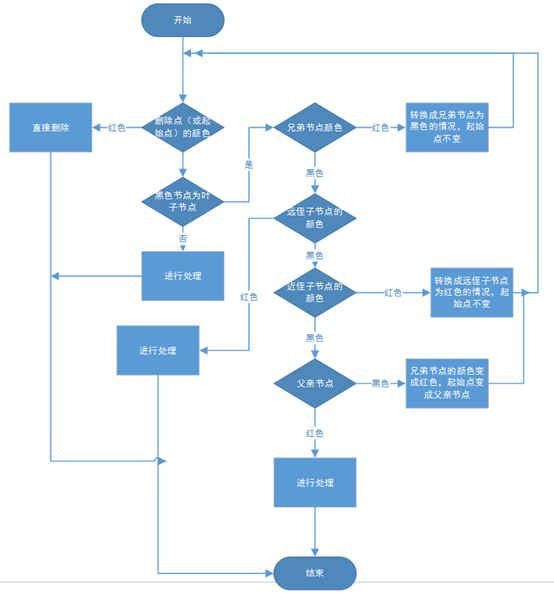
删除节点的思路来自:红黑树之删除节点 - 青儿哥哥 - 博客园 (cnblogs.com)
代码实现
注:删除节点的代码没有进行完整测试
public class RedBlackTree {
public static final boolean RED = false;
public static final boolean BLACK = true;
public Node root;
//删除节点,若有相同值的节点,删除找到的第一个节点
public void delete(int value) {
if (root == null) {
return;
}
Node node = root.search(value);//找待删除的结点node
if (node == null) {//没有找到
return;
} else if (node == root && !(node.left != null && node.right != null)) {//删除root且只有一棵子树
deleteRoot(node);//方法内已经调整结构
return;
}
if (node.left != null && node.right != null) {//待删除节点有两个棵子树
Node successor = successor(node);//获取node后继节点
node.value = successor.value;//后继节点覆盖node,待删除节点变为后继节点,转化为最多一颗右子树的情况
if (node.left == null && node.right == null) {
deleteLeaf(successor);//删除叶子节点
} else {
deleteSingleTree(successor);//删除节点只有一棵子树
}
} else {//待删除节点最多一棵子树
if (node.left == null && node.right == null) {
deleteLeaf(node);//删除叶子节点
} else {
deleteSingleTree(node);//删除节点只有一棵子树
}
}
}
//删除后修复结构
public void deleteFix(Node parent, Node bro) {
if (parent == null || bro == null) {
return;
}
if (bro.color == RED) {//兄弟节点为红色,必有两个黑色子节点,父节点必定为黑色
bro.color = BLACK;
parent.color = RED;
if (bro == parent.right) {//兄弟节点在右方
leftRotate(parent);
bro = parent.right;
}
if (bro == parent.left) {//兄弟节点在左方
rightRotate(parent);
bro = parent.left;
}
} else {//bro.color == BLACK,兄弟节点为黑色
if (parent.color == RED) {//若父节点为红色,兄弟节点和兄弟节点的两个子节点(只能为null)都为黑色
parent.color = BLACK;
bro.color = RED;
return;
} else if (parent.color == BLACK) {//若父节点,兄弟节点和兄弟节点的两个子节点(只能为null)都为黑色的情况
bro.color = RED;
if (parent.parent != null && parent == parent.parent.left) {
bro = parent.right;
} else if (parent.parent != null && parent == parent.parent.right) {
bro = parent.left;
}
parent = parent.parent;
deleteFix(parent, bro);
return;
}
if (bro == parent.right) {//兄弟节点在右方
if (bro.left.color == RED && bro.right.color == BLACK) {//只有一个红色近侄子节点
bro.left.color = BLACK;
bro.color = RED;
rightRotate(bro);
bro = parent.right;
}
if (bro.right.color == RED) {//有一个红色远侄子节点
boolean temp = parent.color;
parent.color = bro.color;
bro.color = temp;
bro.right.color = BLACK;
leftRotate(parent);
}
return;
}
if (bro == parent.left) {//兄弟节点在左方
if (bro.right.color == RED && bro.left.color == BLACK) {//只有一个红色近侄子节点
bro.right.color = BLACK;
bro.color = RED;
leftRotate(bro);
bro = parent.left;
}
if (bro.left.color == RED) {//有一个红色远侄子节点
boolean temp = parent.color;
parent.color = bro.color;
bro.color = temp;
bro.left.color = BLACK;
rightRotate(parent);
}
return;
}
}
}
//删除叶子节点
public void deleteLeaf(Node node) {
if (node.left == null && node.right == null) {
Node parent = node.parent;//前面排除了root的情况,parent一定不为空
Node bro = null;
boolean color = node.color;//记录删除叶子节点的颜色
if (node == parent.left) {
bro = parent.right;
node.parent.left = null;
} else if (node == parent.right) {
bro = parent.left;
node.parent.right = null;
}
if (color == BLACK) {//删除黑色叶子节点才调整
deleteFix(parent, bro);
}
}
}
//删除root,root最多一棵子树的情况
public void deleteRoot(Node node) {
if (node.left != null) {
root = node.left;
root.color = BLACK;
} else if (node.right != null) {
root = node.right;
root.color = BLACK;
} else {
root = null;
}
}
//删除只有一棵子树的节点,此节点必为黑色
public void deleteSingleTree(Node node) {
Node parent = node.parent;
Node bro = null;
if (node.right != null && node.left == null) {
node.right.color = BLACK;
node.right.parent = parent;
if (node == parent.left) {//node在父节点的left
bro = parent.right;
parent.left = node.right;
} else if (node == parent.right) {//node在父节点的right
bro = parent.left;
parent.right = node.right;
}
deleteFix(parent.parent, bro);
} else if (node.left != null && node.right == null) {
node.left.color = BLACK;
node.left.parent = parent;
if (node == node.parent.left) {//node在父节点的left
bro = parent.right;
parent.left = node.left;
} else if (node == parent.right) {//node在父节点的right
bro = parent.right;
parent.right = node.left;
}
deleteFix(parent.parent, bro);
}
}
//返回node后继节点
public Node successor(Node node) {
Node target = node.right;
if (target.left != null) {//parent的右子节点有左子节点
node = node.right;
target = target.left;
while (target.left != null) {//循环的查找左节点,直到找到最小值
node = node.left;
target = target.left;
}
node.left = target.right;//删除该最小值节点,此时target没有左右子节点或只有右节点
} else {//target.left == null,parent的右子节点没有有左子节点
node.right = target.right;//删除该最小值节点,此时target没有左右子节点或只有右节点
}
return target;
}
//返回node前驱节点
public Node precursor(Node node) {
Node target = node.left;
if (target.right != null) {//parent的左子节点有右子节点
node = node.left;
target = target.right;
while (target.right != null) {//循环的查找右节点 直到找到最大值
node = node.right;
target = target.right;
}
node.right = target.left;//删除该最大值节点,此时target没有左右子节点或只有左节点
} else {//target.right == null,parent的左子节点没有有右子节点
node.left = target.left;//删除该最大值节点,此时target没有左右子节点或只有左节点
}
return target;
}
//添加节点,若有相同值的节点,则插入相同值节点的尾部
public void add(Node node) {
if (root == null) {
root = node;
root.color = BLACK;
} else {
root.add(node);
root.addFix(node, this);
}
}
//左旋转
public void leftRotate(Node node) {
Node newNode = node.right;
node.right = newNode.left;
if (newNode.left != null) {
newNode.left.parent = node;
}
if (node.parent == null) {
root = newNode;
} else if (node.parent.left == node) {
node.parent.left = newNode;
} else {//node.parent.right == newNode
node.parent.right = newNode;
}
newNode.left = node;
newNode.parent = node.parent;
node.parent = newNode;
}
//右旋转
public void rightRotate(Node node) {
Node newNode = node.left;
node.left = newNode.right;
if (newNode.right != null) {
newNode.right.parent = node;
}
if (node.parent == null) {//newNode代替node成为新root
root = newNode;
} else if (node.parent.left == node) {
node.parent.left = newNode;
} else {//node.parent.right == newNode
node.parent.right = newNode;
}
newNode.right = node;
newNode.parent = node.parent;
node.parent = newNode;
}
}
class Node {
public int value;
public Node left;
public Node right;
public Node parent;
public boolean color;//节点初始默认为红色,false
public static final boolean RED = false;
public static final boolean BLACK = true;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
", color=" + color +
'}';
}
//添加非根节点后修复树结构
public void addFix(Node node, RedBlackTree redBlackTree) {
if (node == redBlackTree.root) {
node.color = true;
redBlackTree.root = node;
return;
}
Node parent = node.parent;
if (parent.color == BLACK) {//父节点为黑色,直接插入
return;
}
Node grand = parent.parent;//祖父若存在,必定为黑色
Node uncle;
if (grand != null) {
if (grand.left == parent) {
uncle = grand.right;//叔节点在父节点右方
} else {//grand.right == parent
uncle = grand.left;//叔节点在父节点左方
}
if (uncle == null || uncle.color == BLACK) {//叔节点为空或为黑色
if (grand.left == parent && parent.right == node) {//插入节点、父节点、祖父节点成三角
redBlackTree.rightRotate(parent);//右旋转父节点,使父节点变成插入节点的子节点,插入节点、父节点、祖父节点成直线
node.color = BLACK;
grand.color = RED;
redBlackTree.rightRotate(grand);//右旋转祖父节点,使父节点、祖父节点变成插入节点的子节点
} else if (grand.right == parent && parent.left == node) {//插入节点、父节点、祖父节点成三角
redBlackTree.leftRotate(parent);//左旋转父节点,使父节点变成插入节点的子节点,插入节点、父节点、祖父节点成直线
node.color = BLACK;
grand.color = RED;
redBlackTree.leftRotate(grand);//左旋转祖父节点,使父节点、祖父节点变成插入节点的子节点
}
if (grand.left == parent && parent.left == node) {//插入节点、父节点、祖父节点成直线
parent.color = BLACK;
grand.color = RED;
redBlackTree.rightRotate(grand);//右旋转祖父节点,使插入节点、祖父节点变成父节点的子节点
} else if (grand.right == parent && parent.right == node) {//插入节点、父节点、祖父节点成直线
parent.color = BLACK;
grand.color = RED;
redBlackTree.leftRotate(grand);//左旋转祖父节点,使插入节点、祖父节点变成父节点的子节点
}
} else {//叔节点为红色
uncle.color = BLACK;
parent.color = BLACK;
grand.color = RED;
addFix(grand, redBlackTree);//祖父节点按插入节点的情况向上递归处理变色
}
}
}
//添加节点
public void add(Node node) {
if (node == null) {
return;
}
if (node.value < value) {
if (left == null) {
left = node;
node.parent = this;
} else {
left.add(node);
}
} else if (node.value > this.value) {
if (right == null) {
right = node;
node.parent = this;
} else {
right.add(node);
}
} else {//若是相同节点,则不变
return;
}
}
//查找节点,value:节点的值;找到则返回该节点,否则返回null
public Node search(int value) {
if (value == this.value) {//找到该节点
return this;
} else if (value < this.value) {
if (this.left == null) {
return null;
} else {
return this.left.search(value);//向左子树递归查找
}
} else {//value >= this.value
if (this.right == null) {
return null;
} else {
return this.right.search(value);//向右子树递归查找
}
}
}
}
性质
1、所有基于红黑树的符号表实现都能保证操作的运行时间为对数级别(范围查找除外,它所需的额外时间和返回的键的数量成正比)
2、一棵大小为 N 的红黑树的高度不会超过 2 * lgN
3、一棵大小为 N 的红黑树中,根结点到任意结点的平均路径长度为 1.00 * lgN
4、在一棵红黑树中,以下操作在最坏情况下所需的时间是对数级别的:查找、插入、查找最小键、查找最大键、向下取整(找出小于等于该键的最大键)、向上取整(找出大于等于该键的最小键)、排名(找出小于指定键的键的数量)、选择(找出排名为 k 的键)、删除最小键、删除最大键、删除、范围查询




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战