二叉树
概念
1、二叉树:本身是有序树,树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2

(1)二叉树中,第 i 层最多有 2i - 1 个节点
(2)如果二叉树的深度为 k(第 1 层深度为 1),那么此二叉树最多有 2k - 1 个节点
(3)二叉树中,叶子节点数为 n0,度为 2 的节点数为 n2,则 n0 = n2 + 1
(4)对于一个二叉树来说,除了度为 0 的叶子节点和度为 2 的节点,剩下的就是度为 1 的节点(设为 n1),那么总节点 n = n0 + n1 + n2,同时,对于每一个节点来说都是由其父节点分支表示的,假设树中分枝数为 B,那么总节点数 n = B + 1,而分枝数是可以通过 n1 和 n2 表示的,即 B = n1 + 2 * n2,所以,n 用另外一种方式表示为 n = n1 + 2 * n2 + 1,两种方式得到的 n 值组成一个方程组,就可以得出 n0 = n2 + 1
2、满二叉树:如果二叉树中除了叶子节点,每个节点的度都为 2,则此二叉树称为满二叉树
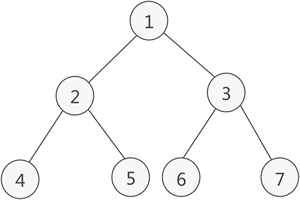
(1)满二叉树中第 i 层的节点数为 2i - 1 个
(2)深度为 k 的满二叉树(第 1 层深度为 1)必有 2k - 1 个节点 ,叶子数为 2k - 1
(3)满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层
(4)具有 n 个节点的满二叉树的深度为 log2(n + 1)
3、完全二叉树
(1)二叉树的深度为 k,除第 k 层外,其它各层 (1~k-1) 的节点数都达到最大个数,第 k 层所有的节点都连续集中在最左边,即在左边连续
(2)如果二叉树中除去最后一层节点为满二叉树,且最后一层的节点依次从左到右分布,则此二叉树被称为完全二叉树
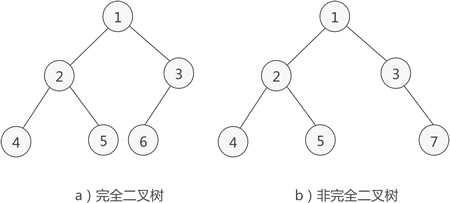
(3)注意:满二叉树是完全二叉树的特殊形态,满二叉树肯定是完全二叉树,而完全二叉树不一定是满二叉树
(4)n 个节点的完全二叉树的深度为 ⌊log2n⌋ + 1 = ⌈log2(n + 1)⌉,⌊log2n⌋ 表示取小于 log2n 的最大整数。例如,⌊log24⌋ = 2,而 ⌊log25⌋ 结果也是 2
(5)对于任意一个完全二叉树来说,如果将含有的节点按照层次从左到右依次标号,对于任意一个节点 i
当 i > 1 时,父亲结点为结点 [i / 2](i = 1 时,表示的是根结点,无父亲结点)
如果 2 * i > n(总结点的个数) ,则结点 i 肯定没有左孩子(为叶子结点);否则其左孩子是结点 2 * i
如果 2 * i + 1 > n ,则结点 i 肯定没有右孩子;否则右孩子是结点 2 * i + 1(6)已知叶子节点数为 n,则总节点为 2 * n
(7)已知总节点数为 n,若 n 为偶数,则叶子节点数为 n / 2,若 n 为奇数,则叶子节点数为 (n + 1) / 2
(8)对 n 个节点数的完全二叉树进行顺序编号,编号 i(1 <= i <= n)
当 i = 1 时,该节点为根,它无双亲节点
当 i > 1 时,该节点的双亲节点的编号为 i / 2
若 2 * i <= n,则有编号为 2 * i 的左叶子,否则没有左叶子
若 2 * i + 1 <= n,则有编号为 2 * i + 1的右叶子,否则没有右叶子(9)深度为 k 的完全二叉树(第 1 层深度为 1)至少有 2k - 1 个结点;至多有 2k - 1结点
树、森林、二叉树的转换
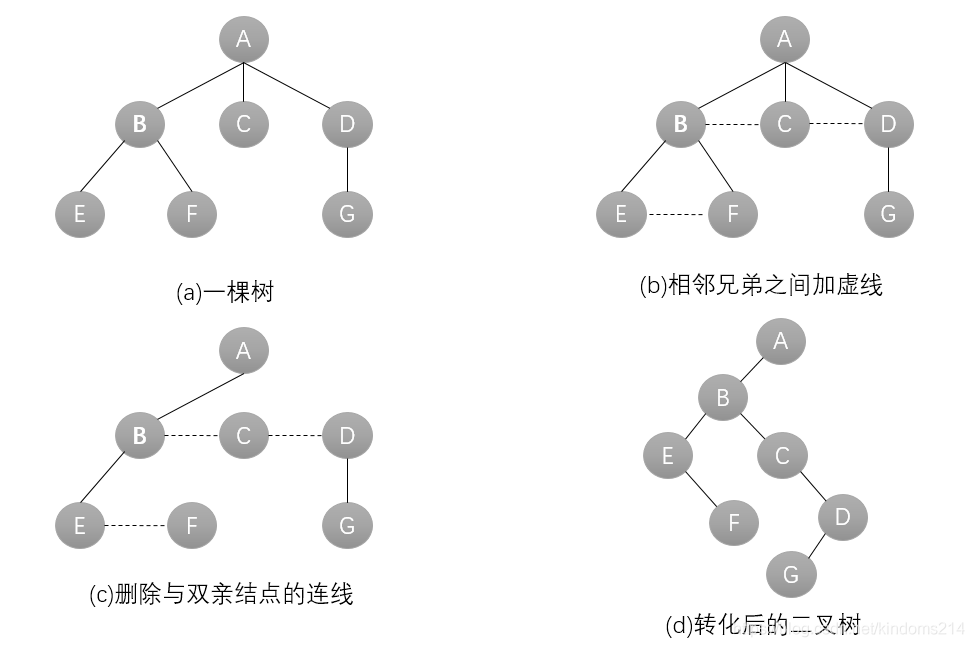
1、树转换为二叉树
(1)加线,在所有兄弟节点之间加一条连线
(2)抹线,对树中的每个节点,只保留它与第一个子节点(最左侧的子节点)之间的连线,删除它与其它子节点之间的连线
(3)旋转,以树的根节点为轴心,将整棵树顺时针转动 45°,使之结构层次分明
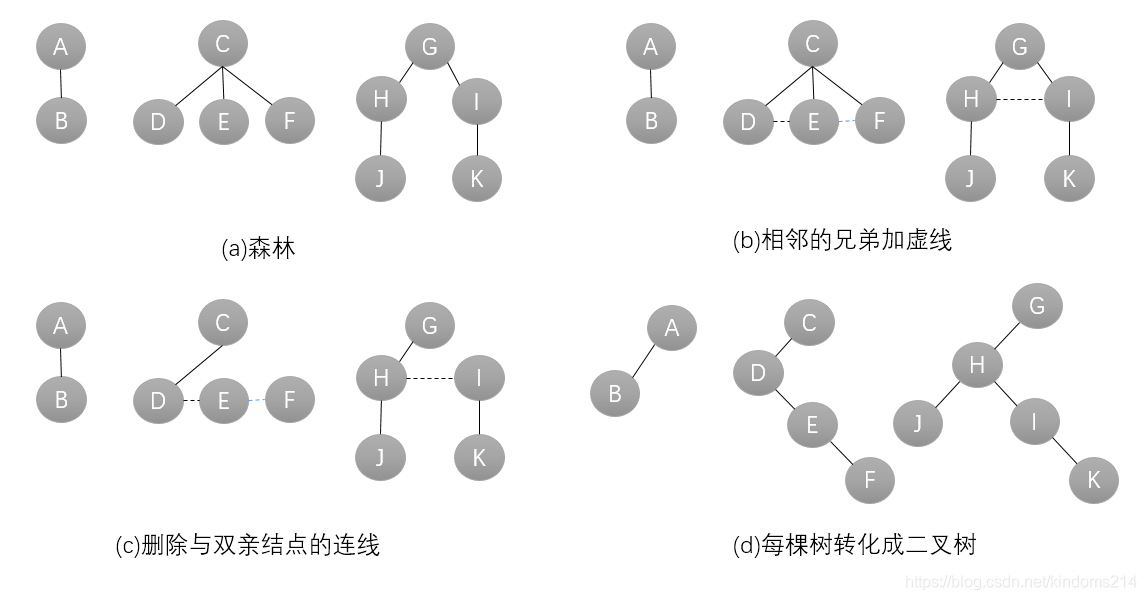
2、森林转换为二叉树
(1)先把每棵树转换为二叉树
(2)第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根节点作为前一棵二叉树的根节点的右子节点,用线连接起来
(3)重复(2),当所有的二叉树连接起来后得到的二叉树就是由森林转换得到的二叉树
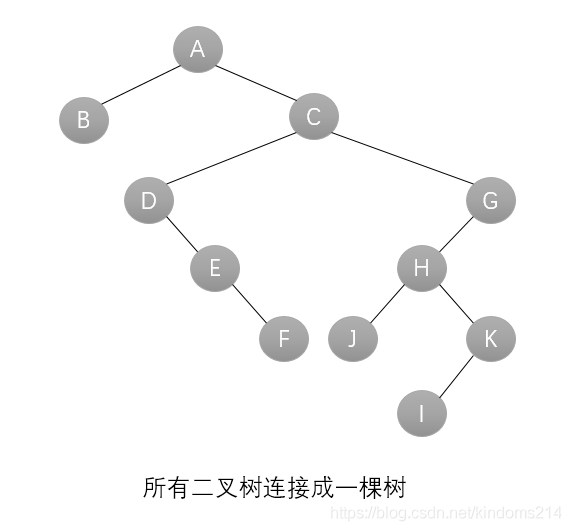
3、二叉树转换为树
(1)若某节点的左子节点存在,将左子节点的右子节点、右子节点的右子节点……都作为该节点的子节点,将该节点与这些右孩子节点用线连接起来
(2)删除原二叉树中所有节点与其右孩子节点的连线
(3)整理(1)和(2)两步得到的树,以该结点为轴心,逆时针转动 45°,使之结构层次分明
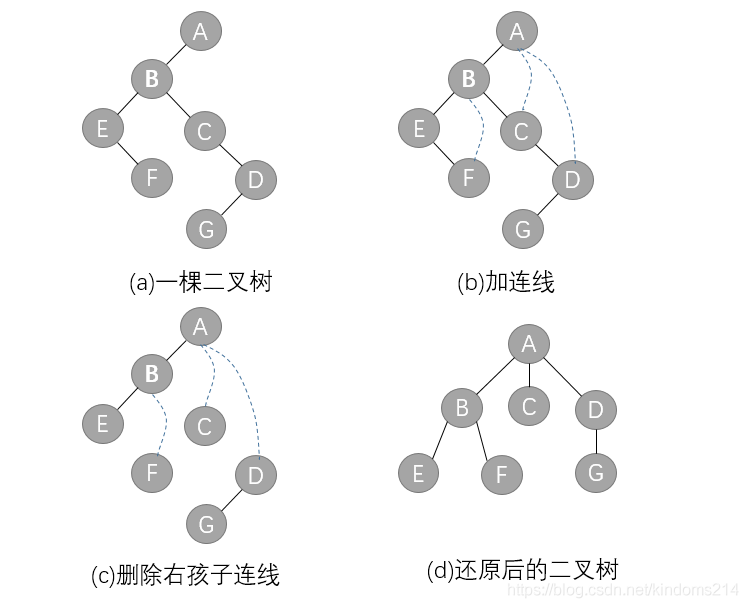
4、二叉树转换为森林
(1)从根节点开始,若右孩子存在,则把与右子节点的连线删除,再查看分离后的二叉树,若其根节点的右孩子存在,则连续删除,直到所有这些根结点与右孩子的连线都删除为止
(2)把分离后的每棵二叉树转换为树
(3)整理第(2)步得到的树,使之规范,这样得到森林
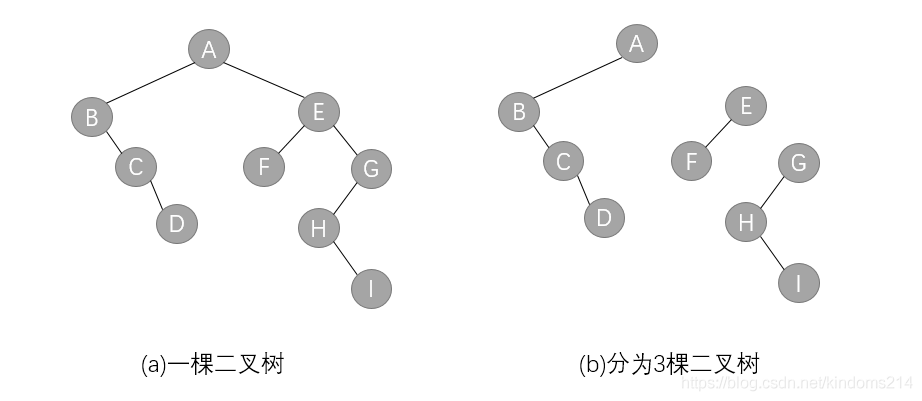
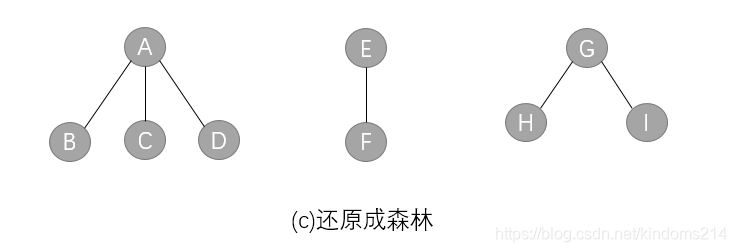
二叉树的遍历
1、前序遍历: 先输出父节点, 再遍历左子树和右子树
(1)输出当前节点(初始是root节点)
(2)若左子节点不为空,则递归继续前序遍历
(3)若右子节点不为空,则递归继续前序遍历
2、中序遍历: 先遍历左子树, 再输出父节点, 再遍历右子树
(1)若左子节点不为空,则递归继续中序遍历
(2)输出当前节点
(3)若右子节点不为空,则递归继续中序遍历
3、后序遍历: 先遍历左子树, 再遍历右子树, 最后输出父节点
(1)若左子节点不为空,则递归继续后序遍历
(2)若右子节点不为空,则递归继续后序遍历
(3)输出当前节点
二叉树的查找
1、前序查找
(1)判断当前节点是否为要查找的节点,若是,则返回当前节点
(2)若否,判断当前节点的左子节点是否为空,若左子节点不为空,则左递归前序查找,找到就返回节点,否则返回null
(3)若左子节点为空,判断当前节点的右子节点是否为空,若右子节点不为空,则右递归前序查找,找到就返回节点,否则返回null
2、中序查找
(1)判断当前节点的左子节点是否为空,若左子节点不为空,则左递归中序查找,找到就返回节点,否则返回null
(2)若左子节点为空,判断当前节点是否为要查找的节点,若是,则返回当前节点
(3)若否,判断当前节点的右子节点是否为空,若右子节点不为空,则右递归中序查找,找到就返回节点,否则返回null
3、后序查找
(1)判断当前节点的左子节点是否为空,若左子节点不为空,则左递归后序查找,找到就返回节点,否则返回null
(2)若左子节点为空,判断当前节点的右子节点是否为空,若右子节点不为空,则右递归后序查找,找到就返回节点,否则返回null
(3)判断当前节点是否为要查找的节点,若是,则返回当前节点,否则返回null
二叉树的删除
1、规定
(1)如果删除的节点是叶子节点, 则删除该节点
(2)如果删除的节点是非叶子节点, 则删除该子树
2、实现思路
二叉树中执行:
(1)先判断根节点root是不是待删除的节点,如果是,则删除根节点,否则开始执行递归
节点中执行:
(2)二叉树是单向的,判断当前节点的子节点是否需要删除节点,而不能去判断当前这个节点是不是需要删除节点
(3)判断当前节点的左节点是否为待删除的节点,如果是,this.left == null,然后返回,结束递归
(4)判断当前节点的右节点是否为待删除的节点,如果是,this.right == null,然后返回,结束递归
(5)否则继续执行左递归,左递归执行完后没有找到该节点,执行右递归,右递归执行完后没有找到该节点,说明二叉树中不存在该节点
代码实现
//定义BinaryTree二叉树
public class BinaryTree {
public Node root;
public void delete(int no) {//删除叶子节点或子树
boolean flag = false;//辅助变量,删除成功就设置为true,默认为false
if (root != null) {//判断树是否为空
if (root.no == no) {//如果只有一个root结点, 这里立即判断root是不是就是要删除结点
root = null;
} else {//进入递归
root.delete(no, flag);
}
} else {
System.out.println("空树,不能删除~");
}
}
//前序遍历
public void preList() {
if (this.root != null) {
this.root.preList();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
//中序遍历
public void infixList() {
if (this.root != null) {
this.root.infixList();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
//后序遍历
public void postList() {
if (this.root != null) {
this.root.postList();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
//前序查找
public Node preSearch(int no) {
if (root != null) {
return root.preSearch(no);
} else {
return null;
}
}
//中序查找
public Node infixSearch(int no) {
if (root != null) {
return root.infixSearch(no);
} else {
return null;
}
}
//后序查找
public Node postSearch(int no) {
if (root != null) {
return this.root.postSearch(no);
} else {
return null;
}
}
}
class Node {
public int no;
public String name;//视作data
public Node left;//默认null
public Node right;//默认null
public Node(int no, String name) {
this.no = no;
this.name = name;
}
@Override
public String toString() {
return "Node{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
public void delete(int no, boolean flag) {
if (flag) {//flag为true,删除成功,结束递归;flag为false,继续递归
return;
}
//如果当前结点的左子结点不为空,并且左子结点就是要删除结点,就将this.left = null; 并且结束递归
if (this.left != null && this.left.no == no) {
this.left = null;
flag = true;//删除成功
return;
}
//如果当前结点的右子结点不为空,并且右子结点就是要删除结点,就将this.right= null ;并且结束递归
if (this.right != null && this.right.no == no) {
this.right = null;
flag = true;//删除成功
return;
}
if (this.left != null) {//向左子树进行递归删除
this.left.delete(no, flag);
}
if (this.right != null) {//向右子树进行递归删除
this.right.delete(no, flag);
}
}
//前序遍历查找
public Node preSearch(int no) {
if (this.no == no) {//判断当前节点
return this;
}
Node node = null;
if (this.left != null) {//左递归
node = this.left.preSearch(no);
}
if (node != null) {//左子树找到
return node;
}
if (this.right != null) {//右递归
node = this.right.preSearch(no);
}
return node;//右子树找到或该节点不存在
}
//中序遍历查找
public Node infixSearch(int no) {
Node node = null;
if (this.left != null) {//左递归
node = this.left.infixSearch(no);
}
if (node != null) {//左子树找到
return node;
}
if (this.no == no) {//判断当前节点
return this;
}
if (this.right != null) {//右递归
node = this.right.infixSearch(no);
}
return node;//右子树找到或该节点不存在
}
//后序遍历查找
public Node postSearch(int no) {
Node node = null;
if (this.left != null) {//左递归
node = this.left.postSearch(no);
}
if (node != null) {//左子树找到
return node;
}
if (this.right != null) {//右递归
node = this.right.postSearch(no);
}
if (node != null) {//右子树找到
return node;
}
if (this.no == no) {
return this;
}
return node;//要查找的就是当前节点或节点不存在
}
//前序遍历
public void preList() {
System.out.println(this);//先输出父结点
if (this.left != null) {//递归向左子树前序遍历
this.left.preList();
}
if (this.right != null) {//递归向右子树前序遍历
this.right.preList();
}
}
//中序遍历
public void infixList() {
if (this.left != null) {//递归向左子树中序遍历
this.left.infixList();
}
System.out.println(this);//输出父结点
if (this.right != null) {//递归向右子树中序遍历
this.right.infixList();
}
}
//后序遍历
public void postList() {
if (this.left != null) {//递归向左子树后序遍历
this.left.postList();
}
if (this.right != null) {//递归向右子树后序遍历
this.right.postList();
}
System.out.println(this);//输出父结点
}
}




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战