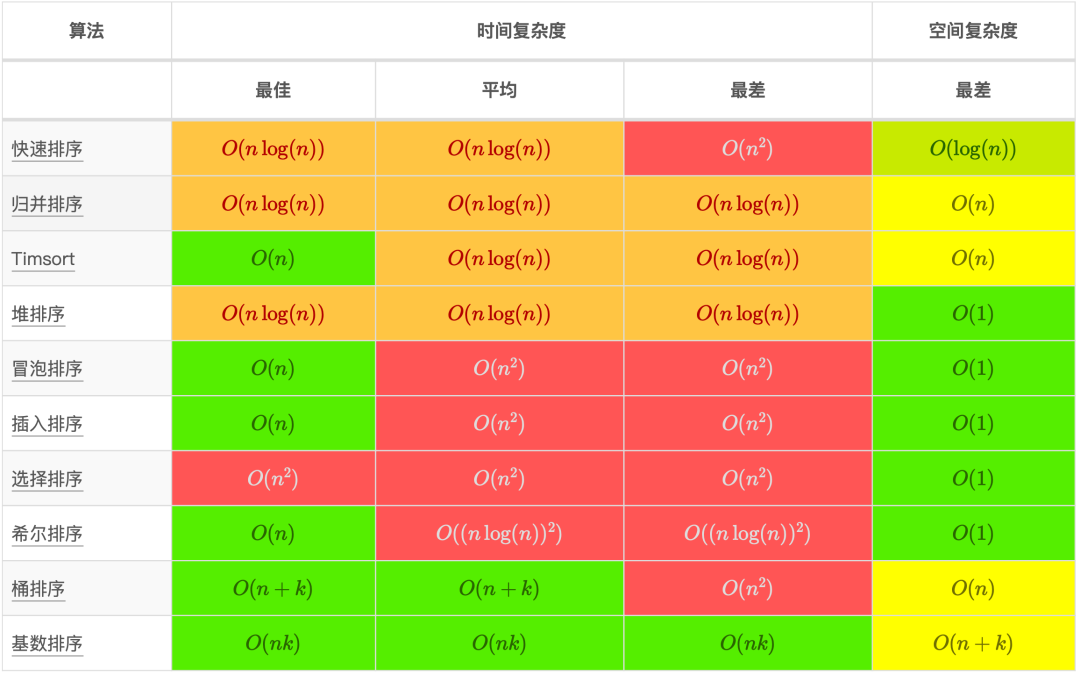
排序算法对比
1、稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面
2、不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面
3、k:“桶”的个数
4、In-place:不占用额外内存
5、Out-place:占用额外内存
补充
1、希尔排序
(1)希尔排序的平均时间复杂度和最坏时间复杂度与间距序列的选取有关,设间距序列为 H,以下两种选取方式均使得排序算法的复杂度降为 O(n2) 级别
(2) 命题 1:若间距序列为 H = {2k - 1 | k = 1, 2,..., ⌊log2n⌋}(从大到小),则希尔排序算法的时间复杂度为 O(n3 / 2)
命题 1:若间距序列为 H = {2k - 1 | k = 1, 2,..., ⌊log2n⌋}(从大到小),则希尔排序算法的时间复杂度为 O(n3 / 2)
(3)命题 2:若间距序列为 H = {k = 2P * 3q | p, g ∈ N, k <= n}(从大到小),则希尔排序算法的时间复杂度为 O(n * log2n)
(4)最差时间复杂度:O(n2)
2、与关键字的初始序序无关的是
(1)元素的移动次数:归并排序、基数排序
(2)元素的比较次数:选择排序、基数排序、折半插入排序
(3)时间复杂度:选择排序、堆排序、归并排序、基数排序
(4)排序趟数:除了快速排序,优化后的冒泡排序(标志位跳出外循环),其他的排序算法都是
3、每一次排序之后都能确定至少一个元素位置的排序方法包括
(1)选择排序:每次将最值放到头 / 尾
(2)冒泡排序:与选择排序相同,每一次排序确定一个最值
(3)快排:每一次排序确定 pivot 的位置
(4)堆排序:每一次排序时,都是将堆顶的元素和最后一个节点互换,然后调整堆,再将堆大小减 1,所以每一次排序确定堆顶元素
4、不能至少确定一个元素的位置的方法包括
(1)插入排序:不到最后一步求的都是相对位置
(2)Shell 排序:对简单插入排序的改进,不到最后一步,无法确定每个元素位置
(3)归并排序:局部有序,并不能确定任一元素在全局的位置
(4)计数排序、桶排序、基数排序:利用桶排序的思路,不是基于比较的排序,也无法在一次排序中确定某个元素的位置,因为每一次排序都是整体处理




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战