稀疏矩阵
稀疏矩阵(二维数组)
1、矩阵中分布有大量的元素 0,即非 0 元素非常少
2、稀疏矩阵的压缩存储,数据结构提供有 3 种具体实现方式:
(1)三元组顺序表
(2)行逻辑链接的顺序表
(3)十字链表
三元组顺序表(压缩存储稀疏矩阵)
1、记录数组一共有几行几列,有多少个不同的值
2、把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模
3、至少需要存储以下信息
(1)矩阵中各非 0 元素的值,以及所在矩阵中的行标和列标
(2)矩阵的总行数和总列数
4、例
(1)稀疏矩阵
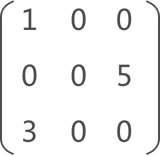
(2)存储的是三元组(即由 3 部分数据组成的集合),组中数据分别表示(行标,列标,元素值),这里矩阵的行标和列标都从 1 开始,省略一组(行数,列数,非 0 数据个数)

转换思路
1.稀疏矩阵转换三元组顺序表
(1)遍历原始稀疏矩阵,得到有效数据的个数sum
(2)创建三元组顺序表 sparseArr int[sum+1][3]
(3)将稀疏矩阵的有效数据存入到三元组顺序表中
2.三元组顺序表转换稀疏矩阵
(1)先读取三元组顺序表的第一行(下标为0的一维数组)
(2)根据第一行的数据,创建原始的稀疏矩阵 int[][] arr = new int[row][col]
(3)再读取三元组顺序表后几行的数据,并赋给原始的稀疏矩阵
3、代码实现
public class SparseArray {//假设二维数组中一维数组的长度一致
//二维数组转稀疏数组
public static int[][] dyadicToSparse(int[][] dyadicArray) {
int sum = 0;//二维数组非0数据个数
for (int i = 0; i < dyadicArray.length; i++) {
for (int j = 0; j < dyadicArray[i].length; j++) {
if (dyadicArray[i][j] != 0) {
sum++;
}
}
}
int[][] sparseArray = new int[sum + 1][3];
sparseArray[0][0] = dyadicArray.length;//二维数组行数
sparseArray[0][1] = dyadicArray[0].length;//二维数组列数
sparseArray[0][2] = sum;//记录非0数据个数
int count = 0;//记录是第几个非0数据
for (int i = 0; i < dyadicArray.length; i++) {
for (int j = 0; j < dyadicArray.length; j++) {
if (dyadicArray[i][j] != 0) {
count++;
sparseArray[count][0] = i;//非0数据的所在行
sparseArray[count][1] = j;//非0数据所在列
sparseArray[count][2] = dyadicArray[i][j];//非0数据的值
}
}
}
return sparseArray;
}
//稀疏数组转二维数组
public static int[][] sparseToDyadic(int[][] sparseArray) {
int dyadicArray[][] = new int[sparseArray[0][0]][sparseArray[0][1]];
for (int i = 1; i < sparseArray.length; i++) {
dyadicArray[sparseArray[i][0]][sparseArray[i][1]] = sparseArray[i][2];
}
return dyadicArray;
}
}
行逻辑链接的顺序表(压缩存储稀疏矩阵)
1、三元组顺序表每次提取指定元素都需要遍历整个数组,运行效率很低
2、行逻辑链接的顺序表在三元组顺序表的基础上提高了查找某一行非 0 数据的效率
(1)行逻辑链接的顺序表和三元组顺序表的实现过程类似,它们存储矩阵的过程完全相同,都是将矩阵中非 0 元素的三元组(行标、列标和元素值)存储在一维数组中
(2)但为了提高提取查找指定行非 0 元素的效率,前者在存储矩阵时比后者多使用了一个数组,专门记录矩阵中每行第一个非 0 元素在一维数组(三元组)中的位置
3、稀疏矩阵示意图

(1)将矩阵中的非 0 元素采用三元组的形式存储到一维数组 data 中(和三元组顺序表一样)

(2)使用数组 rpos(假设索引从 1 开始)记录矩阵中每行第一个非 0 元素在一维数组(三元顺序表)中的存储位置

(3)rpos[i] == j,表示矩阵第 i 行第一个非 0 元素在三元顺序表中的下标为 j
4、若查找矩阵中第 2 行所有的非 0 元素
(1)如果使用三元组顺序表,就必须从头遍历数组中的每个三元组,逐个进行判断
(2)如果使用行逻辑链接的顺序表,借助 rpos 数组可以直接获得数组第 2 行首个非 0 元素在数组中的位置,还可以获得第 2 行最后一个元素在数组中的位置,查找效率大大提升
十字链表(压缩存储稀疏矩阵)
1、对于压缩存储稀疏矩阵,无论是使用三元组顺序表,还是使用行逻辑链接的顺序表,归根结底是使用数组存储稀疏矩阵
2、介于数组“不利于插入和删除数据”的特点,以上两种压缩存储方式都不适合解决类似“向矩阵中添加或删除非 0 元素”的问题
3、例如,A 和 B 分别为两个矩阵,在实现“将矩阵 B 加到矩阵 A 上”的操作时,矩阵 A 中的元素会发生很大的变化,之前的非 0 元素可能变为 0,而 0 元素也可能变为非 0 元素。对于此操作的实现,之前所学的压缩存储方法就显得力不从心
4、存储方式采用的是“链表 + 数组”结构
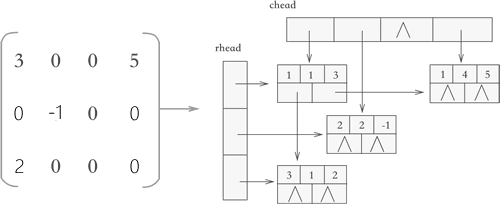
(1)使用十字链表压缩存储稀疏矩阵时,矩阵中各行各列的元素都用一条链表存储,与此同时,将所有行链表的表头存储到一个数组(rhead),将所有列链表的表头存储到另一个数组(chead)中
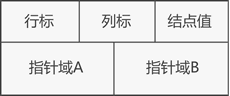
(2)两个指针域分别指向所在行的下一个元素和所在列的下一个元素




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战