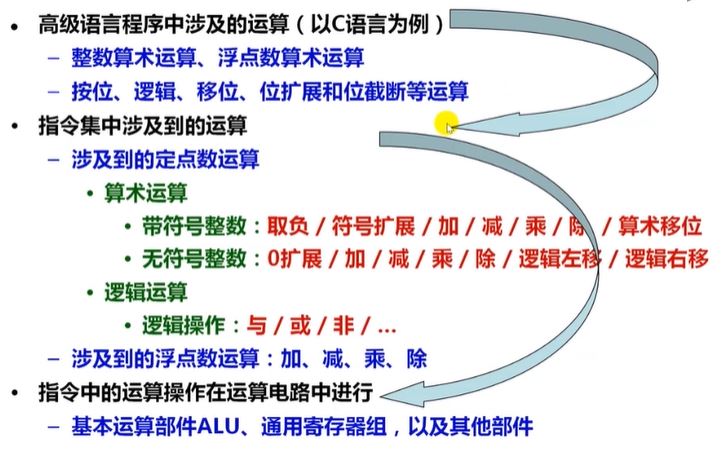
计算机组成原理学习（四）算数逻辑电路，各类运算

上篇链接：https://www.cnblogs.com/banmei-brandy/p/12299962.html

这一部分是比较好理解的，上学时都了解过。

 

---

 

1.与、或、非、异或门

 基本的逻辑运算没什么好记录的，注意符号长啥样。

异或门可以理解为输入的两个值相同则输出0，不同则输出1。

 

2.四个应用

（1）求反

非运算可以对某个特定位，或者全部反转。

（2）使特定的位复位

这里涉及到一个“掩码”的概念，就是1串01序列，和输入数据按位做与运算，因为与运算的特性，会将特定位复位（置为0）。

如对 1010 0110，使用掩码 0000 0111，则输出的结果是0000 0110。掩码中为0的部分会被复位，1的部分不变。

（3）对特定的位置位

和上面类似，是或运算的应用，掩码中为1的部分会被置位（设为1），0的部分不变。

如对 1010 0110，使用掩码 1111 1000，则输出的结果是1111 1110。

（4）使特定的位反转

异或运算的应用，掩码中为1的部分都会取反。

如对 1010 0110，使用掩码 1111 1000，输出的结果是0101 1110。

 

3.n位加法器

用基本逻辑部件构成加法器，A和B是输入的两个数，F是本位的计算结果，Cout是向高位的进位。串联在一起就构成n位加法器。

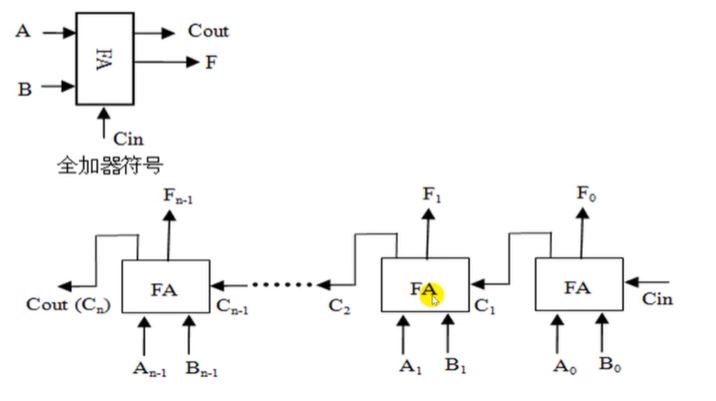
n位加法器可以输出标志信息。

如果要求做减法，减法就是A加上B的补码。求B的补码等于对B取反再加1，这些都可以用逻辑门电路实现。

和加法整合在一起，可以用一个控制信号Sub来决定是做加法还是减法。从图中可以看到Sub相当于求补码时取反后要加上的1。

 

 

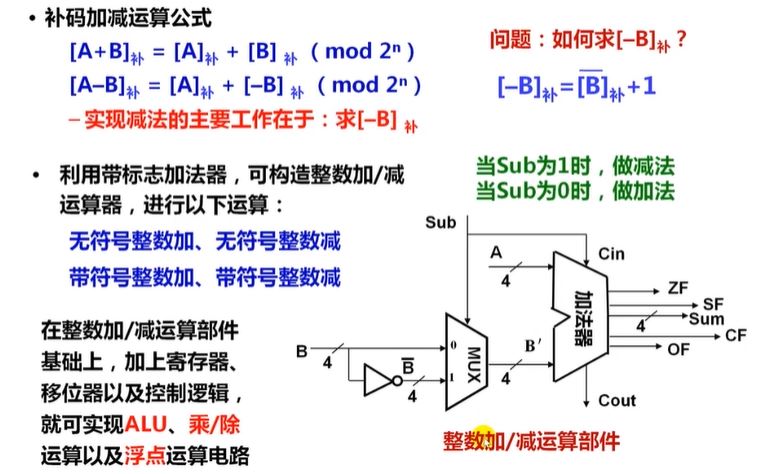
4.移位运算

逻辑移位，左移高位会被丢弃，低位自动补0；右移低位会被丢弃，高位自动补0。

循环移位，不管是左移还是右移都不会丢弃，而是补上尾巴的部分，相当于数据在旋转。如左移一位，最低位就会补上原来的最高位。

算数移位，区分无符号和带符号的数。对于无符号型值，算术移位等同于逻辑移位。而对于有符号型值 ，算术左移等同于逻辑左移，算术右移补的是符号位，正数补0，负数补1。

 

按位与运算，移位运算都用来提取数据（提取的数据不变，其它为0）。

自己换算一下，算数移位其实也可以用来在不改变符号的情况下，做倍数运算。因为差1位相差的就是2的倍数，右移一位正好就是缩小为1/2，左移就是放大到2倍。

 

何时会发生溢出？

无符号数使用逻辑移位，左移时如果移出了1，就会发生溢出。（相当于扩大两倍，然后因为受限于位数导致反而变小）

带符号数使用算数移位，和逻辑移位类似，高位移出时就可能溢出。移出去的符号位和新的顶上去的符号位不一致（比如原来1是负的，顶上去的是0，负数变成了正数），就发生了溢出。

 

5.位拓展，位截断运算

位拓展用于长度短的数据类型拓展到长的数据类型，比如short转int。无符号的会在前面补0，带符号的前面会补符号。

位截断用于长转短，因为将高位丢弃了，所以可能发生“溢出”。

课里给出的例子。

例子2。注意把 i 强转成short时，符号位就给丢掉了，变成负数。位拓展时补上符号位，值没有变化。

 

6.ALU构成

n位带标志的加法器是ALU的核心，ALU加上其它部件以后可以进行所有基本的算数运算和逻辑运算。控制信号决定做什么运算，来自控制器。

 

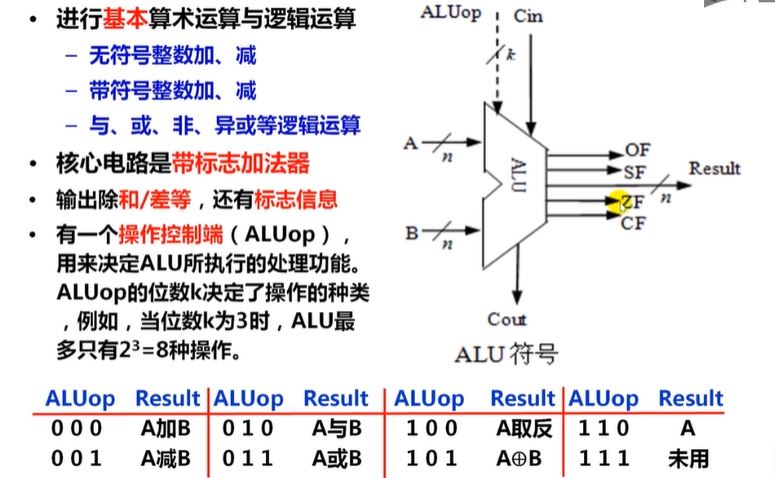
7.源码到电路的过程