计算机组成原理学习（三）整数比较，浮点数的表示

上篇链接：https://www.cnblogs.com/banmei-brandy/p/12299655.html

 

浮点数的表示可能是第一个劝退点，第一遍直接看视频看不懂，因为移码是在前面讲的，和后面没联系起来，讲到后面太快了一时半会理不清，看书却一下子明白了。

 

---

1.基于补码的整数比较

C语言程序中，数据后面带上个“u”或“U”可表示数据是无符号的，用无符号去解释数据。

下面的整数判断表达式会出现与常识相违背的结果。（32位机器，基于补码编码）

 

 

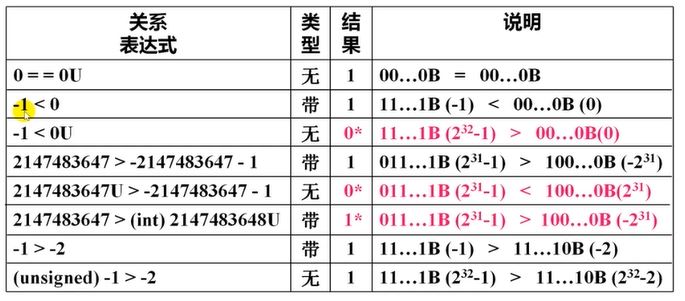
第一条，左边的0的机器数是32位的一串0，右边的机器数也是一串0，加上U用无符号解释一样是0，所以结果为真。

第二条，-1的机器数是32位全部为1，0是32位0，默认带符号比较，-1的机器数的真值为-1，所以比0小，结果为真。

第三条，0带了U，表达式会被解释为无符号来比较，-1机器数的真值变为2^32-1，远比0大，结果为假。

第四条，左边的机器数为首位为0、其余为1的序列，右边的机器数为首位为1，其余为0的序列，按带符号比较，左边真值为最大正数2^31-1，右边为最小负数-2^31，所以结果为真。

第五条，带了U用无符号比较，左边正数不受影响，真值仍然是2^31-1，右边真值变为2^31，所以结果为假。

第六条，左边真值一样不受影响，右边先是带符号，真值解释为2^31，又强转成int，即带符号，真值变成最小负数-2^31，所以结果为真。

第七条，带符号比较，左边真值为-1，右边真值为-2，结果为真。

第八条，左边强转成无符号，真值变成2^32 -1，右边也同理变成2^32 -2，所以结果为真。

 

发现，机器数按无符号去解释，相当于我们平时理解的字面意思，也就是不管编码方式，真值就是二进制正常换算成十进制的值。

 

2.浮点数的编码

实数是包括整数部分和小数部分的数，那啥叫“浮点数”？啥叫“定点数”？

此处的点指的是小数点。如果我用8位去存储实数，假如规定了第一位存符号，后3位存整数，最后4位存小数这种编码方式，那么很明显小数的精度只能到后四位，小数点是固定不变的，这叫“定点数”。

有一个科学计数法表示的十进制数

6.543*10^2

6.543是实数，小数点后面的543是尾数，10是幂，4是指数（阶数）。指数表示了小数点应该向右移动还是向左移动，因为是+2，所有向右移动2格，我们知道这个数字是654.3。这种小数可以移动的实数就叫“浮点数”。

浮点数实际上扩大了存储实数的精度的范围。

类比十进制，假如有二进制实数

1.0111 * 2^3

我们知道这个数是1011.1。

所以理论上说，我们知道尾数部分0.111，指数部分3，还有符号，就能把这个实数表示出来。

 

IEEE754规定计算机中浮点数分为三部分编码：S（Sign符号），E（Exponent指数）和M（Mantissa）。

 

 

S只有一位，0表示正，1表示负。

根据上面的类比，指数部分是有正负的，正表示小数点右移，负表示小数点左移，在计算机中本来也是按有符号数存储，但实际上E指数部分要注意，它是采用移码（也有书上叫余码）编码的，移码说白了就是在原码的基础上，把所有数统一加上一个偏置常数，目的是为了让所有负数和正数都变成正的。

比如有4位可以编码总共16个数字，只使用一个机器数表示0，那么它可表示-7到+8。

假如我们按把它们全部加上7的方式编码，那么它们就会变成0到15，全为正。之后解码时全部减去7即可。7就是偏置常数，也就是说偏置常数的意思就是能够让所有数统一为正的值，或者说与最小负数相加后为0的值。

之所以这样做，是为了对阶比较的方便。

 

 

我们学过十进制的科学计数法比较，就是把指数变成一样的，然后看实数部分就可以了。所以干脆存储时就让指数统一为正。

偏置常数 = 2^(编码位数-1) - 1

M尾数部分的第一位默认为1，是一个隐含部分，不会显示出来。剩下部分就是尾数。

 

3.IEEE标准

IEEE754规定了浮点数单精度和双精度的存储标准。

单精度用32位编码浮点数。S有1位，E有8位，M有23位（首位隐含）。

双精度用64位编码浮点数。S有1位，E有11位，M有52位（首位隐含）。

 

4.浮点数的解码

浮点数的机器数序列串如下，划分好S、E、M三部分后就很容易解码，

S是符号，E要减去一个偏置常数，尾数部分就是小数点后面的值，最后整合起来就行。

 

同理，要把一个十进制实数转换成机器数的步骤——

（1）把十进制数转换成二进制数

（2）二进制数规格化表示（方便区分出SEM三部分）

（3）符号S决定第一位；阶码为E加上偏置常数；M就是规格化表示后的浮点数的尾数部分。

 

5.特殊数的表示

浮点数除了0，,还能把正负无穷等特殊数表示出来。

（1）阶码为全0，尾码也为全0，可以表示为+/-0（看符号位）。

（2）阶码为全0，尾码为全0值，可以表示非规格化的数（之前规格化都是1.xxx*2^x的数，非规格化就是0.xxx*2^x的那一部分非常小的实数）。

（3）正常情况

（4）阶码为全1，尾码为全0，表示正无穷或者负无穷。常出现在一个浮点数除以0的情况。

（5）阶码为全1，尾码为非0，说明这不是一个数。比如sqrt(-4)这种对负数开根号的情况。