勾股定理

勾股定理的计算题型：(在Rt△ABC中,∠C=90º,AB=c,AC=b,BC=a).

一 、已知其中两边,求第三边,如下即为此类题型:

1.如下图，已知OA=OB，那么数轴上点A所表示的数是____________.

2.若直角三角形的两边长分别为3㎝,4㎝，则第三边长为＿＿＿＿＿＿．

3.如图将一根长24㎝的筷子，置于底面直径为5㎝，高为12㎝的圆柱形水杯中，设筷子露在杯子外面的长度是为h㎝,则h的取值范围是 。

4.已知：△ABC中，AB＝13，BC＝10，中线AD＝12.求证：AB＝AC

二、已知一边和一锐角：已知锐角为30º时，已知其相邻的直角边为最难；已知锐角为45º时，已知斜边为最难。难在设边，问题变为解方程，其他的情况都为简单的计算。

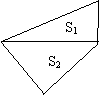
将一副三角板如图放置，上、下两块三角板的面积分别为S₁和S₂ ，则S₁：S₂= ．

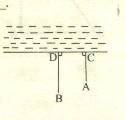
台风是一种自然灾害，它以台风中心为圆心，在周围数十千米范围内形成气旋风暴，有极强的破坏力，据气象观测，距沿海某城市A的正南方向240千米的B处有一台风中心，其中心风力为12级，每远离台风中心25千米，风力就会减弱一级，该台风中心现正以20千米/时的速度沿此偏东30°的方向往C移动，如图所示，且台风中心的风力不变，若城市所受风力达到或超过4级，则称受台风影响．

（1）该城市是否受台风的影响？请说明理由

（2）若会受到台风影响，那么台风影响城市的持续时间有多长？

（3）该城市受到台风影响的最大风力为几级？

如图所示，△ABC中，∠B=45º，∠C=30º，AB=，求：AC的长．

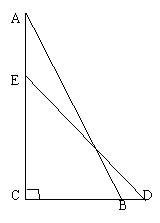
两建筑物水平距离BC=30，从A点测得D点的俯角为30°，测得C点的俯角为60°，求两建筑物的高度（结果保留根号）．

若△ABC中，AB=13,AC=15,高AD=12,则BC的长是（ ）

A.14     B.4    C.14或4    D.以上都不对

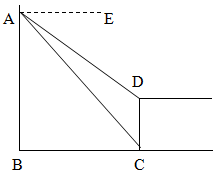
如图所示，一个梯子AB长5米，顶端A靠在墙AC上，这时梯子下端B与墙角C间的距离为3米，梯子滑动后停在DE的位置上，测得DB的长为1米，则梯子顶端A下落了 米。

如图，要在河边修建一个水泵站，分别向张村A和李庄B送水，已知张村A、李庄B到河边的距离分别为2km和7km，且张、李二村庄相距13km．

（1）水泵应建在什么地方，可使所用的水管最短？请在图中设计出水泵站的位置；

（2）如果铺设水管的工程费用为每千米1500元，为使铺设水管费用最节省，请求出最节省的铺设水管的费用为多少元？

 

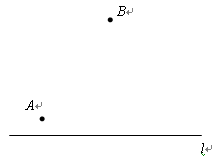
如图，一牧童在A处牧马，牧童家在B处，A、B处距河岸的距离AC，BD的长分别为500米和700米，且CD＝500米，天黑前牧童从A点将马牵到河边去饮水后，再赶回家，那么牧童最少要走＿＿＿＿＿米．

如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点分别按下列要求画三角形和平行四边形．

（1）使三角形三边长为3，，．

（2）使平行四边形有一锐角为45°，且面积为4．

据我国古代《周髀算经》记载，公元前1120年商高对周公说，将一根直尺折成一个直角，两端连结得到一个直角三角形，如果勾是三，股是四，那么弦就等于五。后人概括为“勾三、股四、弦五”.

（1）观察：3，4，5；5，12，13；7，24，25；……，小明发现这些勾股数的勾都是奇数，且从3起就没有间断过，当勾＝3时，股4＝(9-1)，弦5＝(9+1)；

当勾＝5时，股12＝(25-1)，弦13＝(25+1)；

――――――

请你根据小明发现的规律用n(n为奇数且n≥3)的代数式来表示所有这些勾股数的勾、股、弦，并猜想他们之间的相等关系（写二种）并对其中一种猜想加以证明；

(2)继续观察4，3，5；6，8，10；，8，15，17；……，可以发现各组的第一个数都是偶数，且从4起也没有间断过。请你直接用m(m为偶数且m≥4)的代数式来表示他们的股和弦.