图论——EK算法

概念

1. 基本概念
    1.1 流网络，不考虑反向边
    1.2 可行流，不考虑反向边
        1.2.1 两个条件：容量限制、流量守恒
        1.2.2 可行流的流量指从源点流出的流量 - 流入源点的流量
        1.2.3 最大流是指最大可行流
    1.3 残留网络，考虑反向边，残留网络的可行流f' + 原图的可行流f = 原题的另一个可行流
        (1) |f' + f| = |f'| + |f|
        (2) |f'| 可能是负数
    1.4 增广路径
    1.5 割
        1.5.1 割的定义
        1.5.2 割的容量，不考虑反向边，“最小割”是指容量最小的割。
        1.5.3 割的流量，考虑反向边，f(S, T) <= c(S, T)
        1.5.4 对于任意可行流f，任意割[S, T]，|f| = f(S, T)
        1.5.5 对于任意可行流f，任意割[S, T]，|f| <= c(S, T)
        1.5.6 最大流最小割定理
            (1) 可以流f是最大流
            (2) 可行流f的残留网络中不存在增广路
            (3) 存在某个割[S, T]，|f| = c(S, T)
    1.6. 算法
        1.6.1 EK O(nm^2)
        1.6.2 Dinic O(n^2m)
    1.7 应用
        1.7.1 二分图
            (1) 二分图匹配
            (2) 二分图多重匹配
        1.7.2 上下界网络流
            (1) 无源汇上下界可行流
            (2) 有源汇上下界最大流
            (3) 有源汇上下界最小流
        1.7.3 多源汇最大流

EK算法

算法流程

1.先进行bfs，找到一条可行的路径，并记录路径，算出到\(T\)的最大流量\(d[T]\)

2.倒着寻找刚才走过的可行的路径，利用我们记录的\(pre\)数组，从\(T\)开始，每次向前走一个点，即\(i=ver[pre[i] or 1]\)(i是当前所在的点，下同)，因为此时又多扩展的可行流是\(d[T]\),所以\(f[pre[i]]-=d[T],f[pre[i] \ or \ 1]+=d[T]\)

那么算法一定是会结束，因为一个图一定存在一个最大流

算法详细流程

【算法详解】

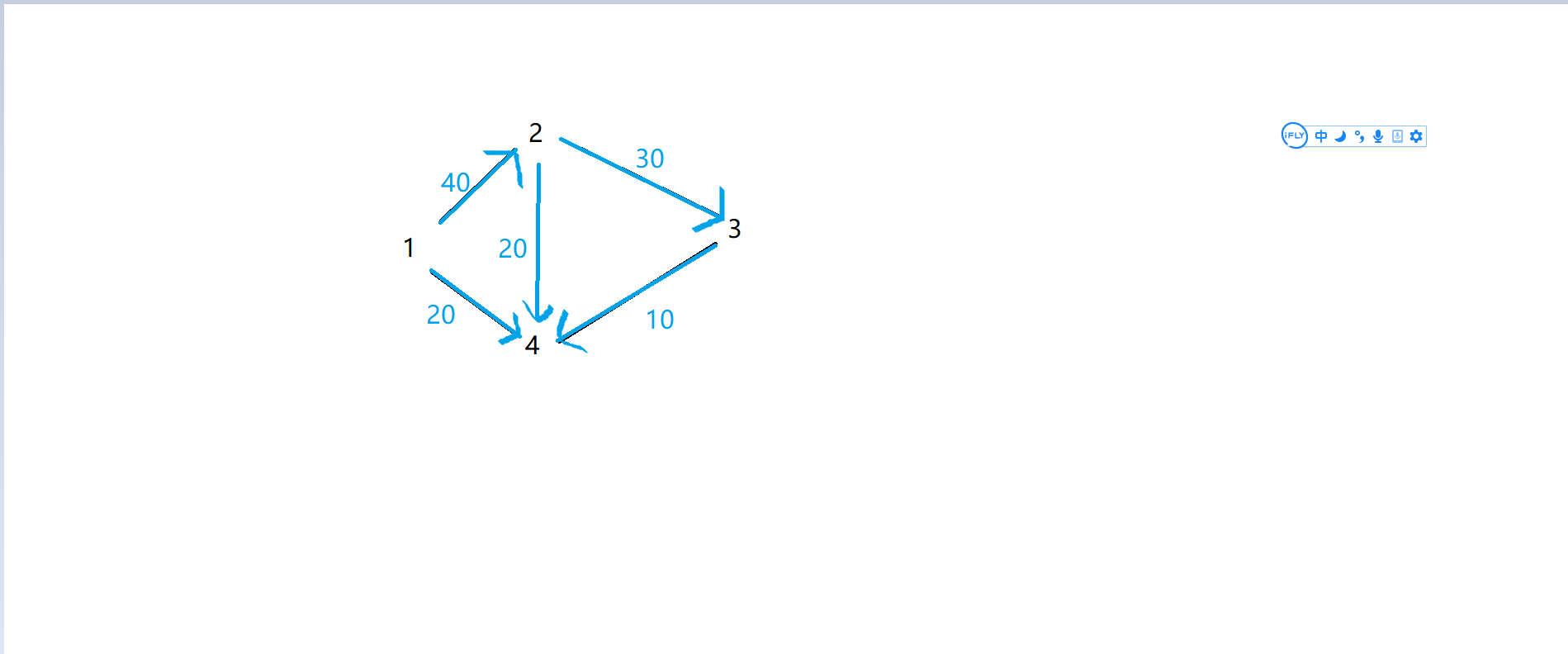
这么一个图，求源点1到汇点4的最大流。

第一轮迭代

将1加入队列，然后将\(st[1]\)设为访问过，把\(d[1]\)的容量设置为正无穷

然后以\(1\)为中心，进行扩展，首先到达\(4\)这个点，因为\(4\)这个点是汇点，所以直接返回此时的可行流\(20\)，将\(st[4]=1\)

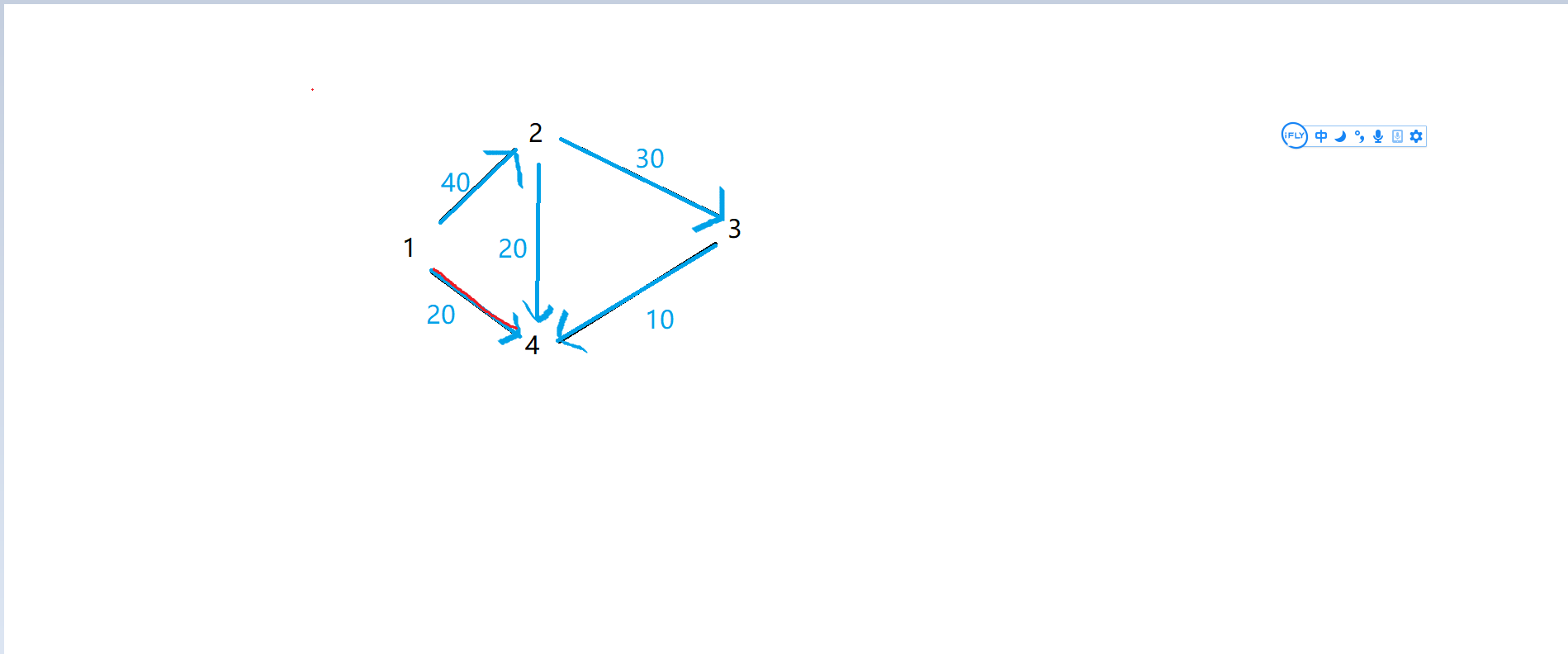
下面我们就需要倒着去寻找路径了，也就是下图中紫色的部分

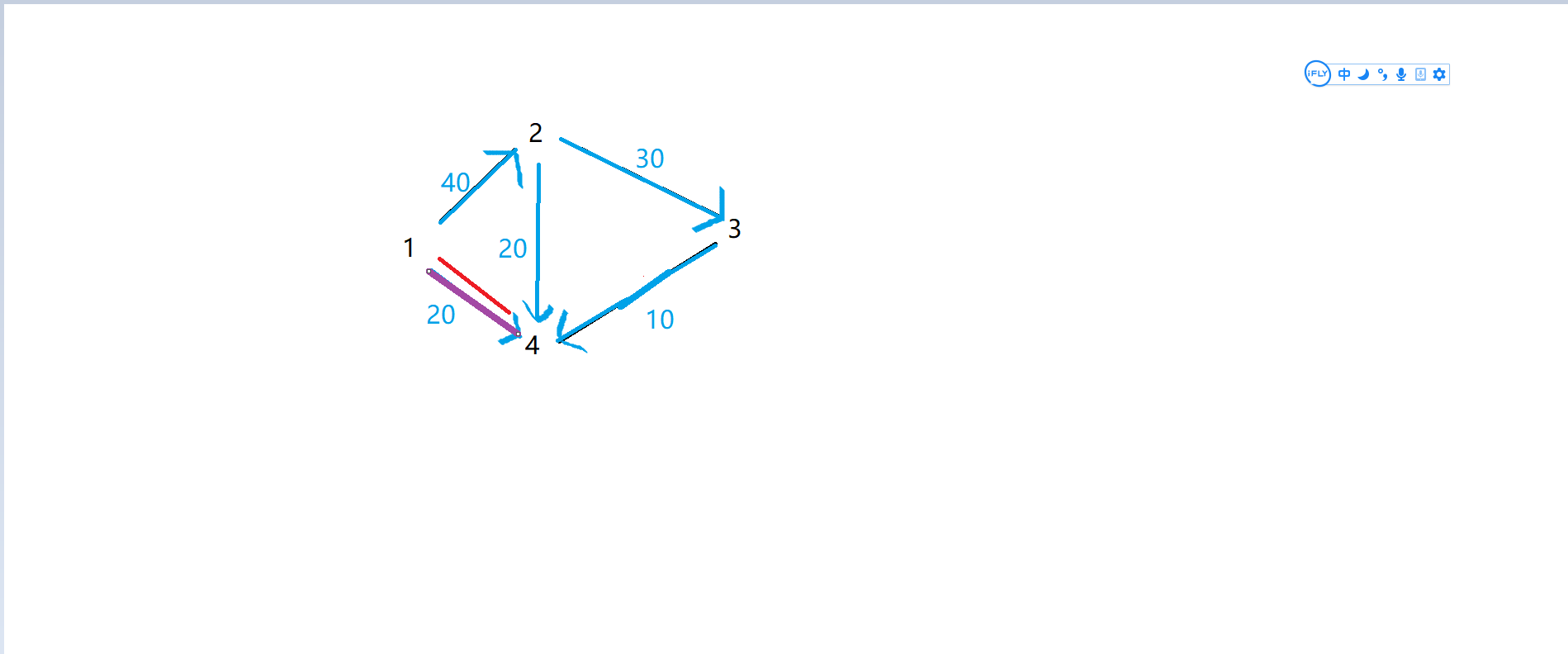
当前点在\(4\)处，\(pre[4]\)是从某个点经过编号为\(pre[4]\)的边，到达4的一个可行流

在这个图中，也就是\(1\)，从\(1——>4\)，此时\(f[从1到4]-=d[T]\)，变成0，\(f[从4到1]+=d[T]\)，变成20。

我们的最大流加上\(d[T]=20\)

接着进行第二轮迭代

首先清空\(st\)数组，将1加入队列，把\(st[1]\)设为1，\(d[1]\)设为正无穷。

以1为中心，向四周进行\(bfs\)，首先遇到4，虽然4没有被访问过，但是由于\(f[从1到4]=0\)，所以从1到4不是一个可行流，跳过4号点。然后遇到了\(2\)，\(2\)没有被访问过，并且\(f[从1到2]>0\)目前是一条可行流，进行拓展，把\(2\)加入队列，并记录路径\(pre[2]=\)从\(1\)到\(2\)的边的标号，\(1\)弹出队列

接着以\(2\)为中心，向四周进行\(bfs\)，首先遇到了\(4\)，\(4\)没有被访问过，并且\(f[从2到4]>0\)，直接返回此时的流量\(20\)，

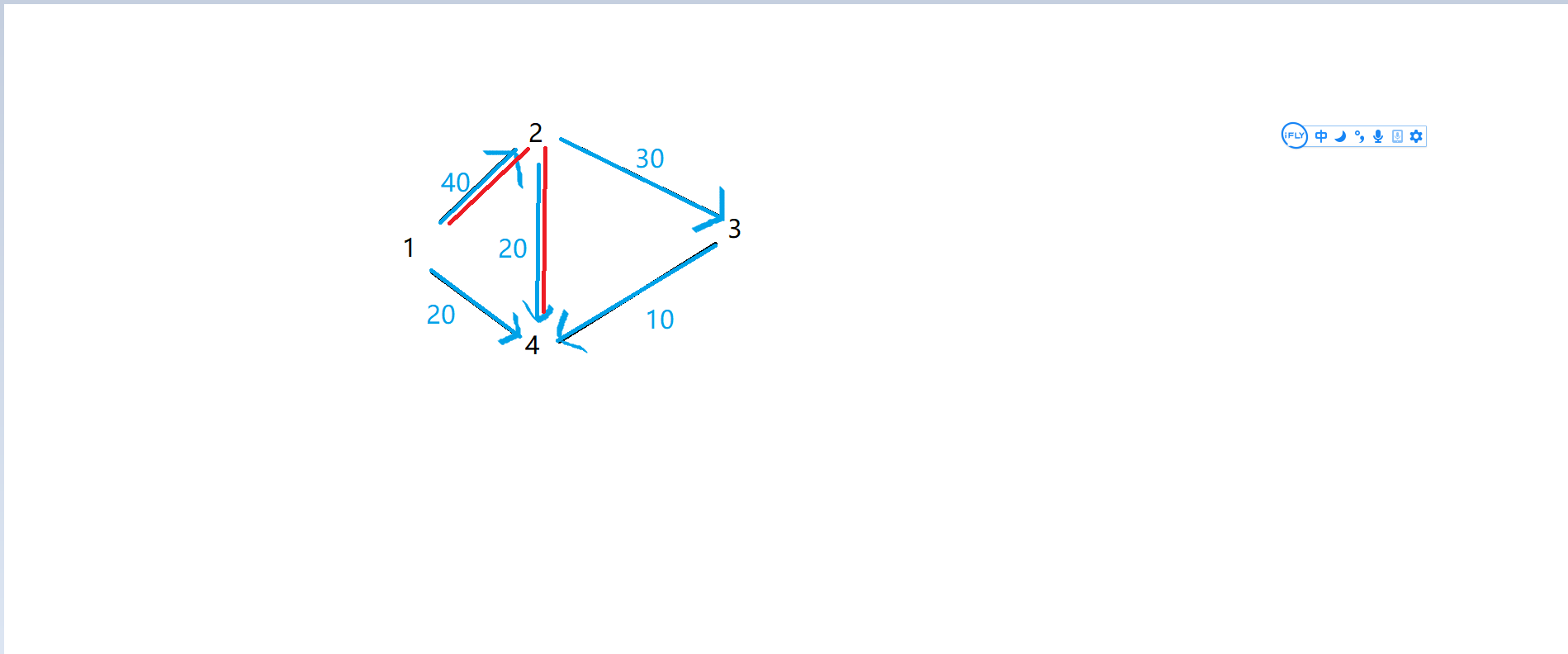
下面的过程跟上面的一样，当前的点在\(4\)处，根据\(pre\)数组找路径，可以知道是从2号点转移过来的，所以\(f[从2到4]-=d[T]\),\(f[从4到2]+=d[T]\)，从1到2的边流量也这样进行更新

如图所示

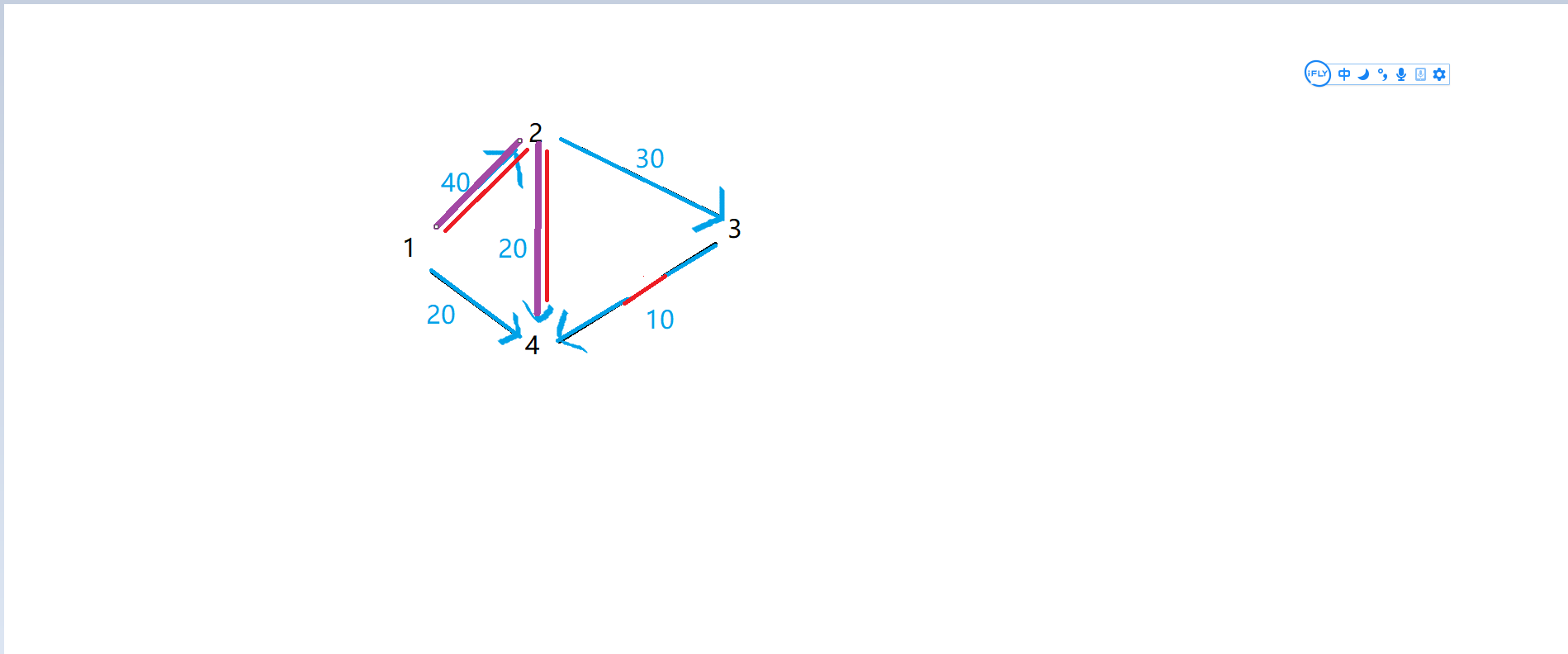
第三轮迭代同理，总是找到当前的可行流，然后更新经过路径上的\(f[ \ ]\)数组......

最后一定会结束迭代

代码

#include<bits/stdc++.h>
using namespace std;
const int N=200000;
int ver[N],head[N],ne[N];
int f[N],d[N];
int idx;
int S,T;
int n,m;
int st[N],pre[N];
#define INF 0x3f3f3f3f
void add(int a,int b,int c)
{
    f[idx]=c,ver[idx]=b,ne[idx]=head[a],head[a]=idx++;
    f[idx]=0,ver[idx]=a,ne[idx]=head[b],head[b]=idx++;
}

bool bfs()
{
    queue<int> q;
    q.push(S);
    d[S]=INF;
    memset(st,false,sizeof(st));
    st[S]=true;
    while(q.size())
    {
        int t=q.front();
        q.pop();
        for(int i=head[t];i!=-1;i=ne[i])
        {
            int j=ver[i];
            if(!st[j]&&f[i])
            {
                st[j]=1;
                d[j]=min(d[t],f[i]);
                pre[j]=i;
                if(j==T)return true;
                q.push(j);
            }
        }
    }
    return false;
}

int EK()
{
    int r=0;
    while(bfs())
    {
        for(int i=T;i!=S;i=ver[pre[i]^1])
        {
            f[pre[i]]-=d[T];
            f[pre[i]^1]+=d[T];
            
        }
        r+=d[T];
    }
    return r;
}
int main()
{
     scanf("%d%d%d%d", &n, &m, &S, &T);
  memset(head, -1, sizeof head);
  while (m--) {
    int a, b, c;
    scanf("%d%d%d", &a, &b, &c);
    add(a, b, c);
  }

  printf("%d\n", EK());
  return 0;
}