【排序法】C语言的排序法

二分插入法

直接插入法

带哨兵的直接排序法

希尔（Shell）排序法

二分插入法

void HalfInsertSort(int a[], int len)
{
     int i, j,temp;
     int low, high, mid;
     for (i=1; i
     {
          temp = a[i];
          low = 0;
          high = i-1;
          while (low <= high)
          {
               mid = (low + high) / 2;
               if (a[mid] > temp)  
               {
                high = mid-1;
               }
               else    
               {
                low = mid+1;
               }
          }      
          for (j=i-1; j>high; j--)
          {
           a[j+1] = a[j];
          }
          a[high+1] = temp;
     }
}

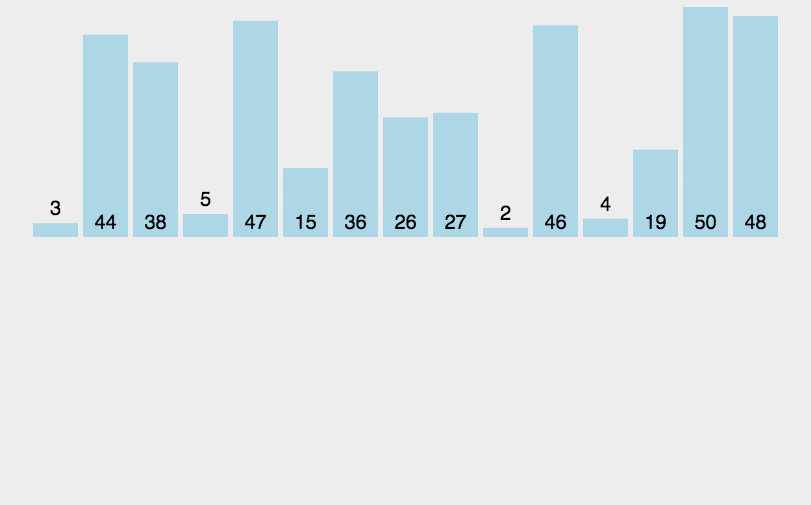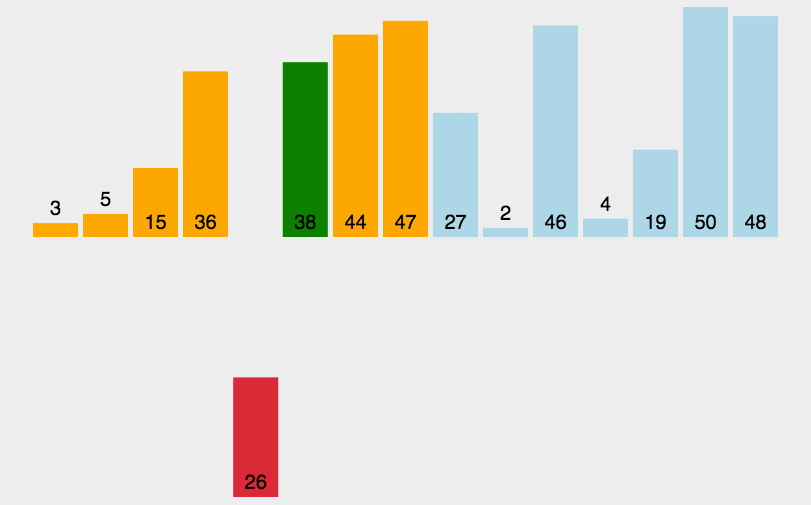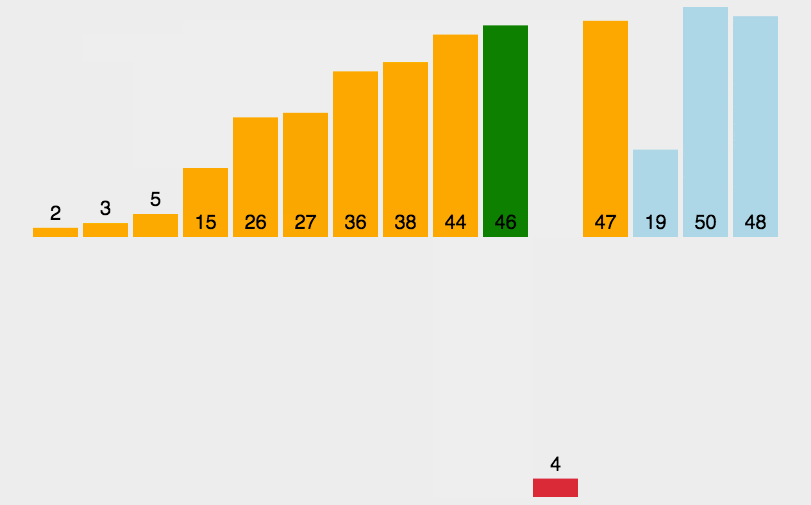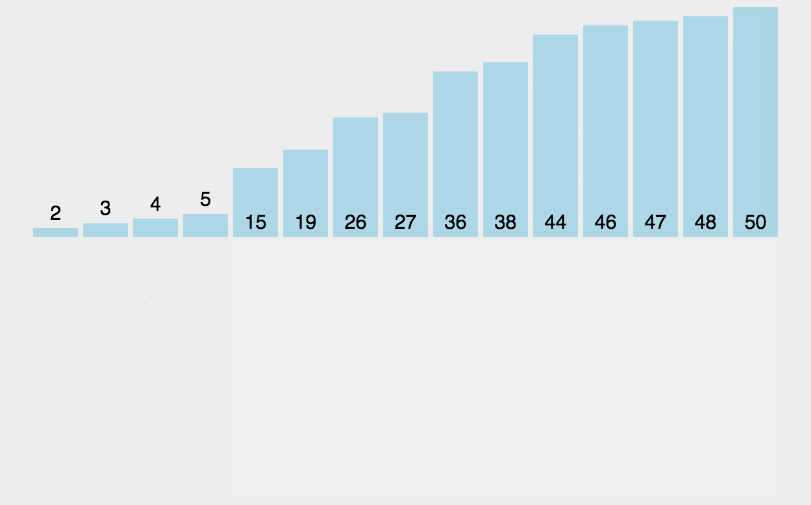
直接插入法

void InsertionSort(int input[],int len) 
{
     int i,j,temp;
     for (i = 1; i < len; i++) 
     {
          temp = input[i];  
          for (j = i - 1;j>-1&&input[j] > temp ; j--)
          {
               input[j + 1] = input[j];
               input[j] = temp;
          }
     }
}

带哨兵的直接排序法

void InsertionSortWithPiquet(int input[],int len) 
{
     int i,j;
     for (i = 2; i < len; i++)  
     {
          input[0] = input[i];
          for (j = i - 1; input[j] > input[0] ; j--) 
          {
               input[j + 1] = input[j];
               input[j] = input[0];
          }
     }
}

希尔（Shell）排序法

#include

void sort(int v[],int n)
{
     int gap,i,j,temp;
     for(gap=n/2;gap>0;gap /= 2)
     {
          for(i=gap;i
          {
               for(j=i-gap;(j >= 0) && (v[j] > v[j+gap]);j -= gap )
               {
                temp=v[j];
                v[j]=v[j+gap];
                v[j+gap]=temp;
               }
          }
     }
}

算法：请看【动画模拟演示】： https://www.bilibili.com/video/BV1p4411L7Yz?from=search&seid=7569363055106581620

冒泡法

void Bublesort(int a[],int n)
{
     int i,j,k;
     for(j=0;j<n;j++)
     {
          for(i=0;i<n-j;i++)
          {
               if(a[i]>a[i+1])  
               {
                    k=a[i];
                    a[i]=a[i+1];
                    a[i+1]=k;
               }
          }
     }
}

选择排序法


void Selectsort(int A[],int n) 
{
     int i,j,min,temp; 
     for(i=0;i
     {
          min=i; 
          for(j=i+1;j<=n;j++)  
          {
               if(A[min]>A[j])  
               {
                temp=A[i]; 
                A[i]=A[j]; 
                A[j]=temp;
               }
          }
    } 
}

快速排序

快速算法

配套动画：https://www.bilibili.com/video/BV1Tt411r75A?from=search&seid=6893000229545682949

void quickSort(int arr[], int left, int right)
{
    if (left > right)
    {
        return;
    }

    int i = left;
    int j = right;
    int pivot = arr[left];
    int tmp   = 0;

    while (i < j)
    {
        while (i < j && arr[j] >= pivot )
        {
            j--;
        }

        while (i < j && arr[i] <= pivot )
        {
            i++;
        }

        if(i < j)   //交换
        {
            tmp    = arr[i];
            arr[i] = arr[j];
            arr[j] = tmp ;
        }
    }

    arr[i] = pivot;

    quickSort3(arr, left, i - 1);
    quickSort3(arr, i + 1, right);
}

//交换的地方也可以用C++的 swap()
#include<algorithm>
swap(arr[i], arr[j]);

快速排序算法优化

隐忧：选取选第一个做pivot，对某些极端分布的数据组，快排效率是比较低的。

改进：最前，最后，中间选择三个元素，取其中的中位数做pivot。经过这样处理，至少保证极端分布是数组，我们选取的pivot不是最小或最大了。

快排还可以优化的，比如随机选取基准值位置而不是永远选第一个。对某些极端分布的数据组，快排效率是比较低的，如果能保证完全随机的话还好，快排的精髓就是选择pivot，这个用rand选和随机选三个数中的中位数是生产中采用的，我也写了个，采用的就是三个数中选择中位数的，

数组选取某个元素都是0(1)的，随机和从整个数组选三个复杂度都差不多，

我现在写的就是从前面选择三个元素，可能有些教材告诉你，从最前，最后，中间选择三个元素，有可能从最后选择三个元素，有可能就是随机选择的三个元素

这样处理之后比取第一个有什么好处

第一个有可能选择的是最小的，或者最大的，经过上面的处理是不是至少保证不会是最小最大了

快排还挺怕这种最大最小的极端情况的

堆排序

void HeapAdjust(int data[],int s,int m)
{ 
     int j,rc; 
     rc=data[s];    
     for(j=2*s;j<=m;j*=2)        
     {
          if(j
          if(rc>data[j]) break; 
          data[s]=data[j];  
          s=j; 
     } 
    data[s]=rc;    
}

void Heap_sort(int data[],int long_n)
{
     int i,temp; 
     for(i=long_n/2;i>0;--i)  
     {
      HeapAdjust(data,i,long_n);
     }
     for(i=long_n;i>0;--i)
     {
      temp=data[1];    
      data[1]=data[i]; 
      data[i]=temp;   
      HeapAdjust(data,1,i-1);
     }
}

动画演示：6分30秒开始：https://www.bilibili.com/video/BV1vt4y1y7wR?from=search&seid=11715982063368022420

清晰的讲解：https://www.bilibili.com/video/BV1Eb41147dK?from=search&seid=719612800024792001