【算法】图

与此同时，为了便于管理这些链表，通常会将所有链表的头节点存储到数组中（也可以用链表存储）。也正因为各个（顶点的）链表的头节点存储的是各个顶点，因此各链表在存储邻接点数据时，仅需存储该邻接点位于数组中的位置下标即可。

例如，存储图 1a) 所示的有向图，其对应的邻接表如图 1b) 所示：

邻接表存储有向图

图 1 邻接表存储有向图

拿顶点 V1 来说，与其相关的邻接点分别为 V2 和 V3，因此存储 V1 的链表中存储的是 V2 和 V3 在数组中的位置下标 1 和 2。

存储内容：

从图 1 中可以看出，存储各顶点的节点结构分为两部分，数据域和指针域。数据域用于存储顶点数据信息，指针域用于链接下一个节点，如图 2 所示：

图 2 邻接表节点结构

在实际应用中，除了图 2 这种节点结构外，对于用链接表存储网（边或弧存在权）结构，还需要节点存储权的值，因此需使用图 3 中的节点结构：

图 3 邻接表存储网结构使用的节点

图 1 中的链接表结构转化为对应 C 语言代码如下：

#define  MAX_VERTEX_NUM 20//最大顶点个数
#define  VertexType int//顶点数据的类型
#define  InfoType int//图中弧或者边包含的信息的类型
typedef struct ArcNode{
    int adjvex;//邻接点在数组中的位置下标
    struct ArcNode * nextarc;//指向下一个邻接点的指针
    InfoType * info;//信息域
}ArcNode;
typedef struct VNode{
    VertexType data;//顶点的数据域
    ArcNode * firstarc;//指向邻接点的指针
}VNode,AdjList[MAX_VERTEX_NUM];//存储各链表头结点的数组
typedef struct {
    AdjList vertices;//图中顶点的数组
    int vexnum,arcnum;//记录图中顶点数和边或弧数
    int kind;//记录图的种类
}ALGraph;

邻接表计算顶点的出度和入度

使用邻接表计算无向图中顶点的入度和出度会非常简单，只需从数组中找到该顶点然后统计此链表中节点的数量即可。

而使用邻接表存储有向图时，通常各个顶点的链表中存储的都是以该顶点为弧尾的邻接点，因此通过统计各顶点链表中的节点数量，只能计算出该顶点的出度，而无法计算该顶点的入度。

对于利用邻接表求某顶点的入度，有两种方式：

遍历整个邻接表中的节点，统计数据域与该顶点所在数组位置下标相同的节点数量，即为该顶点的入度；
建立一个逆邻接表，该表中的各顶点链表专门用于存储以此顶点为弧头的所有顶点在数组中的位置下标。比如说，建立一张图 1a) 对应的逆邻接表，如图 4 所示：

图 4 逆邻接表示意图

对于具有 n 个顶点和 e 条边的无向图，邻接表中需要存储 n 个头结点和 2e 个表结点。在图中边或者弧稀疏的时候，使用邻接表要比前一节介绍的邻接矩阵更加节省空间。

前向星和链式前向星

1、前向星

前向星是以存储边的方式来存储图，先将边读入并存储在连续的数组中，然后按照边的起点进行排序，这样数组中起点相等的边就能够在数组中进行连续访问了。它的优点是实现简单，容易理解，缺点是需要在所有边都读入完毕后下对所有边进行一次排序，带来了时间开销，实用性也较差，只适合离线算法。图一-2-4展示了图一-2-1的前向星表示法。

2、链式前向星（就是数组模拟链表）

链式前向星和邻接表类似，也是链式结构和线性结构的结合，每个结点i都有一个链表，链表的所有数据是从i出发的所有边的集合（对比邻接表存的是顶点集合），边的表示为一个四元组(u, v, w, next)，其中(u, v)代表该条边的有向顶点对，w代表边上的权值，next指向下一条边。

具体的，我们需要一个边的结构体数组 edge[MAXM]，MAXM表示边的总数，所有边都存储在这个结构体数组中，并且用head[i]来指向 i 顶点为起点的第一条边。

边的结构体声明如下：

struct EDGE 
{
  int u, v, w, next;
  EDGE() {}
  EDGE(int _u, int _v, int _w, int _next) 
  {
    u = _u, v = _v, w = _w, next = _next;
  }
}edge[MAXM];

初始化所有的head[i] = INF，当前边总数 edgeCount = 0

每读入一条边，调用addEdge(u, v, w)，具体函数的实现如下：

void addEdge(int u, int v, int w)
 {
     edge[edgeCount] = EDGE(u, v, w, head[u]);
     head[u] = edgeCount ++;
 }

这个函数的含义是每加入一条边(u, v)，就在原有的链表结构的首部插入这条边，使得每次插入的时间复杂度为O(1)，所以链表的边的顺序和读入顺序正好是逆序的。这种结构在无论是稠密的还是稀疏的图上都有非常好的表现，空间上没有浪费，时间上也是最小开销。

调用的时候只要通过head[i]就能访问到由 i顶点出发的第一条边（在数组中）的编号（位置），通过编号到edge数组进行索引可以得到边的具体信息，然后根据这条边的next （因为是倒序的，所以nexxt就是上一条边）域可以得到第二条边的编号，以此类推，直到next域为INF（这里的INF即head数组初始化的那个值，一般取-1即可）。

（https://www.cnblogs.com/DWVictor/p/10279526.html）

链式前向星

head[i]表示以i为起点的第一条边的存储位置。

next[i]表示与第i条边同起点的上一条边的存储位置。（存储和读出的顺序是相反的，所以next是上一条边）

用len[i]来记录所有以i为起点的边在数组中的存储长度.

e[i]表示第i条边的终点。

edge[i].to表示第i条边的终点,

edge[i].next表示与第i条边同起点的上一条边的存储位置,

edge[i].w为边权值.

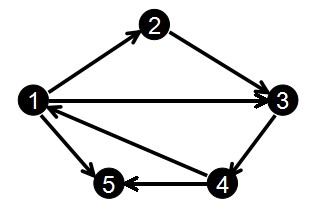
那么对于下图:

我们输入边的顺序为:

1 2

2 3

3 4

1 3

4 1

1 5

4 5

那么排完序后就得到:

1 //以1为起点的边的集合
1 2
1 3
1 5
  
2 //以2为起点的边的集合
2 3 
 
3 //以3为起点的边的集合
3 4 
 
4  //以4为起点的边的集合
4 1 
4 5

即：

编号: 1 2 3 4 5 6 7

起点u: 1 1 1 2 3 4 4

终点v: 2 3 5 3 4 1 5

得到:


head[1] = 1    len[1] = 3       //head[1]，既1为起点的第一条边（1，2）的位置，编号1

head[2] = 4    len[2] = 1

head[3] = 5    len[3] = 1

head[4] = 6    len[4] = 2      //head[4]，既4为起点的第一条边（4，1）的位置，编号6

但是利用前向星会有排序操作,如果用快排时间至少为O(nlog(n))

如果用链式前向星,就可以避免排序.

我们建立边结构体为:

struct Edge
{

     int next;
     int to;
     int w;
};

其中

edge[i].to表示第i条边的终点,

edge[i].next表示与第i条边同起点的下一条边的存储位置,

edge[i].w为边权值.

另外还有一个数组head[],它是用来表示以i为起点的第一条边存储的位置,实际上你会发现这里的第一条边存储的位置其实

在以i为起点的所有边的最后输入的那个编号. （从1开始数）

head[]数组一般初始化为-1,对于加边的add函数是这样的:

void add(int u, int v, int w)
{
    edge[cnt].w = w;

    edge[cnt].to = v;

    edge[cnt].next = head[u];

    head[u] = cnt++;
}

初始化cnt = 0,这样,现在我们还是按照上面的图和输入来模拟一下:

edge[0].to = 2;     edge[0].next = -1;      head[1] = 0;

edge[1].to = 3;     edge[1].next = -1;      head[2] = 1;

edge[2].to = 4;     edge[2],next = -1;      head[3] = 2;

edge[3].to = 3;     edge[3].next = 0;       head[1] = 3;

edge[4].to = 1;     edge[4].next = -1;      head[4] = 4;

edge[5].to = 5;     edge[5].next = 3;       head[1] = 5;

edge[6].to = 5;     edge[6].next = 4;       head[4] = 6;

很明显,head[i]保存的是以i为起点的所有边中编号最大的那个,而把这个当作顶点i的第一条起始边的位置.

这样在遍历时是倒着遍历的,也就是说与输入顺序是相反的,不过这样不影响结果的正确性.

比如以上图为例,以节点1为起点的边有3条,它们的编号分别是0,3,5 而head[1] = 5

我们在遍历以u节点为起始位置的所有边的时候是这样的:

for(int i=head[u];~i;i=edge[i].next)

那么就是说先遍历编号为5的边,也就是head[1],然后就是edge[5].next,也就是编号3的边,然后继续edge[3].next,也

就是编号0的边,可以看出是逆序的.

（链式前向星--最通俗易懂的讲解https://blog.csdn.net/sugarbliss/article/details/86495945）

图论-链式前向星-删边操作

struct edge{
	int fr,to,top,bot;//fr为起点, to为终点, top为边集栈中该边上方一边, bot为边集栈中该边下方一边 
}e[2000005];
int head[2005],ecnt=0;
inline void add_edge(int u, int v){
	e[++ecnt].fr = u;		//编辑起点 
	e[ecnt].to = v;			//编辑终点 
	e[ecnt].top = 0;		//因为新加入的边为栈顶，所以上方不存在边，设为0 
	e[head[u]].top = ecnt;	//原栈顶的上方设为该边
	e[ecnt].bot = head[u];	//该边的下方设为原栈顶 
	head[u] = ecnt;			//新栈顶为该边 
	return ;
}
inline void delete_edge(int now){//now为要删除的边的编号 
	int up=e[now].top, down=e[now].bot;
	if	(up == 0)	head[e[now].fr] = down;//栈顶改变 
	else	e[up].bot = down;	//上方边的下方改变 
	if	(down>0)	e[down].top = up;			//下方边的上方改变 
	return ;
}

posted on 2022-10-04 01:25 bdy 阅读(6) 评论(0) 编辑收藏举报

刷新页面返回顶部

UESTC

【算法】图

图的存储方法

邻接表存储法详解

前向星和链式前向星

链式前向星

图论-链式前向星-删边操作

导航

公告