并查集扩展
并查集扩展
目录
普通并查集
例题:
1.洛谷P1197 星球大战
链接:
[P1197 JSOI2008] 星球大战 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
类型:
普通并查集+反向加点
解析:
正面删边很难,考虑反向求解,先求删完所有要求点的所有连通块数量,然后再一个一个加入,将问题简化
代码:
const int N = 400005;
struct edges{
int v,ne;
}e[N << 1];
int h[N],idx = 0;
void add(int u,int v){
e[idx] = {v,h[u]};
h[u] = idx++;
}
int f[N];
int fd(int x){
if(x==f[x]) return x;
return f[x] = fd(f[x]);
}
int vis[N],ans[N];
int n,m;
void solve(){
memset(h,-1,sizeof h);
cin >> n >> m;
for(int i = 1;i<=n;i++) f[i] = i;
vector<int> b;
for(int i = 1;i<=m;i++){
int u,v;
cin >> u >> v;
u++,v++;
add(v,u);
add(u,v);
}
int k;
cin >> k;
int res = n - k;
for(int i = 0;i<k;i++){
int t;
cin >> t;
t++;
vis[t] = 1;
b.push_back(t);
}
for(int i = 1;i<=n;i++){
if(vis[i]) continue;
for(int j = h[i];~j;j=e[j].ne){
int v = e[j].v;
if(vis[v]) continue;
if(f[fd(i)] != f[fd(v)]){
res--;
f[fd(i)] = f[fd(v)];
}
}
}
ans[k+1] = res;
for(int i = k - 1;i >= 0;i--){
vis[b[i]] = 0;
res++;
for(int j = h[b[i]];~j;j=e[j].ne){
int v = e[j].v;
if(vis[v]) continue;
if(f[fd(b[i])] != f[fd(v)]){
res--;
f[fd(b[i])] = f[fd(v)];
}
}
ans[i + 1] = res;
}
for(int i = 1;i<=k+1;i++){
cout << ans[i] << endl;
}
}
2.洛谷P1955 程序自动分析
链接:
[P1955 NOI2015] 程序自动分析 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
类型:
普通并查集+离散化
解析:
普通并查集判断是否矛盾,数据大进行离散化
代码:
const int N = 200005;
struct DSU {
vector<int> f;
DSU(){}
DSU(int n) {
init(n);
}
void init(int n) {
f.resize(n);
iota(f.begin(), f.end(), 0);
}
int fd(int x) {
if(f[x]==x) return x;
return f[x] = fd(f[x]);
}
bool same(int x, int y) {
return fd(x) == fd(y);
}
bool mg(int x, int y) {
x = fd(x);
y = fd(y);
if (x == y)return false;
f[y] = x;
return true;
}
};
int gt_idx(vector<int>& a,int i){
int t = lower_bound(a.begin(),a.end(),i) - a.begin() + 1;
return t;
}
void solve(){
int n;
cin >> n;
vector<int> v1;
vector<pair<int,int>> ys;
vector<pair<int,int>> ns;
vector<int> a;
for(int i = 0;i < n;i++){
int u,v,op;
cin >> u >> v >> op;
if(op==1){
ys.push_back({u,v});
}else{
ns.push_back({u,v});
}
a.push_back(u);
a.push_back(v);
}
sort(a.begin(),a.end());
a.erase(unique(a.begin(),a.end()),a.end());
int sz = a.size();
DSU d(sz + 1);
for(auto &[u,v]:ys){
d.mg(gt_idx(a,u),gt_idx(a,v));
}
for(auto &[u,v]:ns){
if(d.fd(gt_idx(a,u)) == d.fd(gt_idx(a,v))){
cout << "NO" << endl;
return;
}
}
cout << "YES" << endl;
}
带权并查集
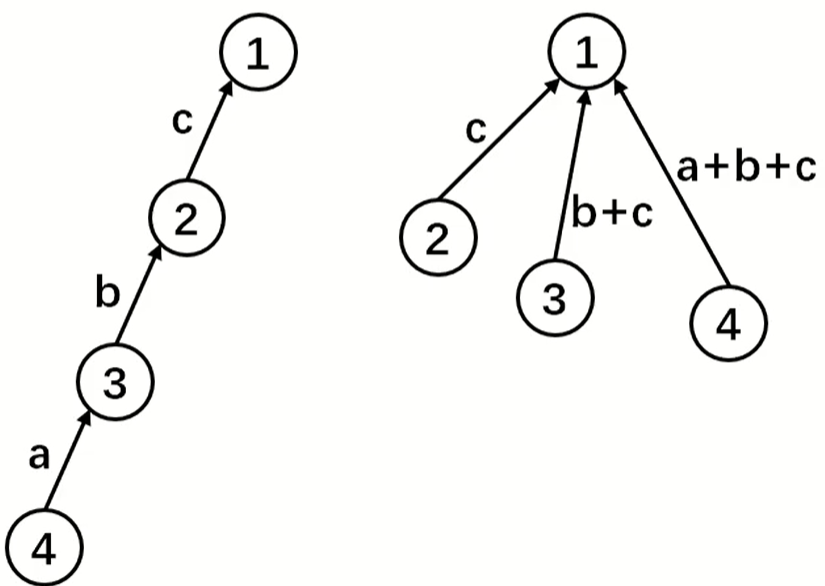
例题:
1.洛谷P2024 食物链
链接:
[P2024 NOI2001] 食物链 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
类型:
带权并查集
解析:
维护%3关系,考虑合并时候维护集合关系,在同类时候d[u] - d[v]在%3意义下一定是0,x吃y那么一定是1,题目无需考虑2的情况,因为没有设置y吃x的正确性
代码:
const int N = 200005;
int f[N],d[N];
int n,m;
int fd(int x){
if(x!=f[x]){
int t = f[x];
f[x] = fd(f[x]);
d[x] += d[t];
}
return f[x];
}
int calc(int x,int y){
return ((x-y)%3 + 3)%3;
}
void merge(int x,int y,int v){
int px = fd(x),py = fd(y);
f[px] = py;
d[px] = d[y] - d[x] + v;
}
void solve(){
cin >> n >> m;
iota(f,f+n+1,0);
int cnt = 0;
while(m--){
int u,v,op;
cin >> op >> u >> v;
if(u>n||v>n){
cnt++;
continue;
}
if(op==1){
if(fd(u)==fd(v) && calc(d[u],d[v]) != 0){
cnt++;
continue;
}
//d[v] = d[u] + d[fd(u)]
//d[fd[u]] = d[v] - d[u]
if(fd(u)!=fd(v)) merge(u,v,0);
}else{
if(fd(u)==fd(v) && calc(d[u],d[v]) != 1){
cnt++;
continue;
}
//d[v] = d[u] - 1 + d[fd(u)]
//d[fd[u]] = d[v] - d[u] + 1
if(fd(u)!=fd(v)) merge(u,v,1);
}
}
cout << cnt << endl;
}
2.洛谷P1196 银河英雄传说
链接:
[P1196 NOI2002] 银河英雄传说 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
类型:
带权并查集
解析:
维护两个变量,一个是集合大小,一个是元素到根的距离,然后操作即可
代码:
const int N = 200005;
int sz[N],d[N],f[N];
void init(){
for(int i = 0; i < N - 1;i++){
f[i] = i;
sz[i] = 1;
}
}
int fd(int x){
if(f[x]!=x){
int t = f[x];
f[x] = fd(f[x]);
d[x] += d[t];
}
return f[x];
}
void merge(int x,int y){
int px = fd(x),py = fd(y);
f[px] = py;
d[px] = sz[py];
sz[py] += sz[px];
}
void solve(){
int q;
init();
cin >> q;
while(q--){
int x,y;
char op;
cin >> op >>x >> y;
if(op=='C'){
if(fd(x)!=fd(y)){
cout <<-1<<endl;
}else{
cout << abs(d[x]-d[y]) - 1 << endl;
}
}else{
merge(x,y);
}
}
}
3.洛谷P5937 Parity Game
链接:
[P5937 CEOI1999] Parity Game - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
类型:
带权并查集
解析:
前缀和思想,合并 y 与 x - 1 判断奇偶性即可
代码:
const int N = 200005;
int n,q;
int idx = 0;
map<int,int> h;
int gt(int x){
if(h.count(x)) return h[x];
h[x] = ++idx;
return idx;
}
int d[N],f[N];
int fd(int x){
if(f[x] != x){
int t = f[x];
f[x] = fd(f[x]);
d[x] += d[t];
}
return f[x];
}
void merge(int x,int y,int v){
int px = fd(x),py = fd(y);
f[px] = py;
d[px] = d[y] - d[x] + v;
}
int calc(int x,int y){
return ((d[x] - d[y])%2 + 2)%2;
}
void solve(){
cin >> n >> q;
int res = q;
for(int i = 0;i<N;i++) f[i] = i;
int id = 0;
while(q--){
int x,y;
++id;
string op;
cin >> x >> y >> op;
if(x==y&&op=="even"){
res = id-1;
break;
}
x = gt(x - 1);
y = gt(y);
if(op=="even"){
if(fd(x)==fd(y)){
if(calc(x,y) == 1){
res = id - 1;
break;
}
}else{
merge(x,y,0);
}
}else{
if(fd(x)==fd(y)){
if(calc(x,y) == 0){
res = id - 1;
break;
}
}else{
merge(x,y,1);
}
}
}
cout << res << endl;
}
扩展域并查集
例题:
1.洛谷P1525 关押罪犯
链接:
[P1525 NOIP2010 提高组] 关押罪犯 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
类型:
扩展域并查集 + 带权并查集
解析:
方法一(扩展域并查集):
- 两个集合,从大到小排序,考虑将敌对两个人分成两个集合,并且扩展域合并,敌人的敌人是朋友,就是设x有两个敌人 y z, 那么 z 与 x+n 建边, x +n 与 y 建边,通过 x+n这个虚点去连接应该在一个集合中的y与z,如果在同一集合,并且是敌对,那么直接输出即可
方法二(带权并查集):
- 从大到小排序,避免前面的数在一个监狱,将两个集合合并起来,并且赋权值为1代表两个数不在同一监狱,于是在后面我们可以判断,如果两个数之前已经合并过并且mod操作位0代表,这两个集合一定要在一个监狱中,那么直接输出w,(否则,w会更大)
代码:
方法一:
int n,m;
struct qs{
int u,v,w;
bool operator<(const qs& q1)const{
return w > q1.w;
}
};
struct DSU {
vector<int> f, sz;
DSU(){}
DSU(int n) {
init(n);
}
void init(int n) {
f.resize(n);
iota(f.begin(), f.end(), 0);
sz.assign(n, 1);
}
int fd(int x) {
if(f[x]==x) return x;
return f[x] = fd(f[x]);
}
bool mg(int x, int y) {
x = fd(x);
y = fd(y);
if (x == y)return false;
f[y] = x;
return true;
}
};
void solve(){
cin >> n >> m;
DSU d(2*(n+1));
vector<qs> q;
for(int i = 0; i < m;i++){
int u,v,w;
cin >> u >> v >> w;
q.push_back({u,v,w});
}
sort(q.begin(),q.end());
for(int i = 0;i < q.size();i++){
int u = q[i].u,v = q[i].v,w = q[i].w;
if(d.fd(u) == d.fd(v)){
cout << w <<endl;
return;
}
d.mg(u,v+n);
d.mg(u+n,v);
}
cout << 0 << endl;
}
方法二:
struct qs
{
int u,v,w;
bool operator<(const qs &t)const{return w > t.w;};
};
int f[N],d[N];
int n,m;
int fd(int x){
if(x!=f[x]){
int t = f[x];
f[x] = fd(f[x]);
d[x] += d[t];
}
return f[x];
}
int calc(int x,int y){
return ((x-y)%2 + 2)%2;
}
void merge(int x,int y){
int px = fd(x),py = fd(y);
f[px] = py;
d[px] = d[y] - d[x] + 1;
}
void solve(){
cin >> n >> m;
int q = m;
vector<qs> a;
iota(f,f+n+1,0);
while(q--){
int u,v,w;
cin >> u >> v >> w;
a.push_back({u,v,w});
}
sort(a.begin(),a.end());
for(int i = 0; i < m;i++){
int u = a[i].u,v = a[i].v,w = a[i].w;
if(fd(u)==fd(v)){
if(calc(d[u],d[v]) == 0){
cout << w << endl;
return;
}
}else{
merge(u,v);
}
}
cout << 0 <<endl;
}
