Atcoder ABC296 F

Atcoder ABC296 F

F - Simultaneous Swap

链接:

F - Simultaneous Swap (atcoder.jp)

简要题意:

• 问题陈述

  给你两个 \(N\) 数字序列： \(A=(A_1,A_2,\ldots,A_N)\) 和 \(B=(B_1,B_2,\ldots,B_N)\) 。

  高桥可以重复下面的操作任意多次(可能为零)。

  在 \(1\) 和 \(N\) 之间选择三个成对的不同整数 \(i\) 、 \(j\) 和 \(k\) 。
  把 \(A\) 的 \(i\) -th 和 \(j\) -th 元素对调，把 \(B\) 的 \(i\) -th 和 \(k\) -th 元素对调。

  如果高桥有办法重复操作使 \(A\) 和 \(B\) 相等，打印 "Yes"；否则，打印 "No"。
  在这里， \(A\) 和 \(B\) 相等的条件是，对于每一个 \(1\leq i\leq N\) ， \(A\) 的 \(i\) 个元素和 \(B\) 的 \(i\) 个元素相等。

思路:

• 首先a与b数组元素不相同的情况下一定是NO

• 我们发现一个重要性质,我们可以保持A不动,只改变B,操作如下
  

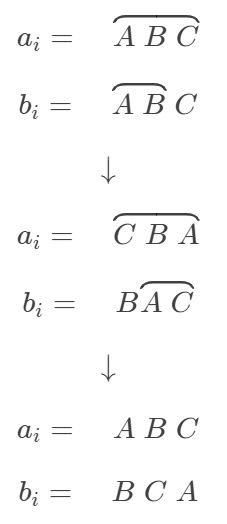
• 我们发现b数组可以循环轮换排列,并且,如果b数组或者a数组有两个相同元素,那么她们可以通过反复横跳使得顺序一致

• 如果两个数组中分别都没有重复元素

• 我们考虑一次上图循环置换顺序,只会让逆序对+2,0,-2,这就意味着奇偶性相同ab数组一定可以转换,反之则不能

代码:

const int N = 200005;
int tr1[N],tr2[N];
int n;
int lb(int x){return x&-x;}
void add(int k,int tr[]){
    for(int i = k;i < N;i+=lb(i)) tr[i]++;
}
int qy(int k,int tr[]){
    int res = 0;
    for(int i = k;i > 0;i-=lb(i)) res+=tr[i];
    return res;
}
void solve(){
    
    cin >> n;
    map<int,int> h1;
    map<int,int> h2;
    int a[n + 1],b[n+1];
    int c1 = 0,c2 = 0;
    for(int i = 1;i<=n;i++){
        cin >> a[i];
        c1+=qy(a[i],tr1);
        add(a[i],tr1);
        h1[a[i]]++;
        
    }
    for(int i = 1;i<=n;i++){
        cin >> b[i];
        c2+=qy(b[i],tr2);
        add(b[i],tr2);
        h2[b[i]]++;
        
    }
    if(h1!=h2){
        cout << "No" << endl;
        return ;
    }
    for(int i = 1;i<=n;i++){
        if(h2[b[i]]>=2||h1[a[i]]>=2){
            cout << "Yes" << endl;
            return;
        }
    }
    if(c1%2!=c2%2){
        cout << "No" << endl;
    }else{
        cout << "Yes" << endl;
    }
 
}