BUAA_OO 第一单元总结 表达式解析与化简
程序结构分析
HW1
数据的组织基本上都是自己一拍脑袋乱想的,没有经过深思熟虑。做这个作业的时候,我的思维还停留在“过了就行,下次重构下次再说”这样……
解析方法参考了第一次实验课的代码。
代码规模
| 类的名称 | 属性个数 | 方法个数 | 行数 |
|---|---|---|---|
| Main | 2 | 6 | 146 |
| Number | 2 | 3 | 18 |
| Term | 2 | 7 | 65 |
| Sum | 2 | 6 | 40 |
| Pow | 2 | 2 | 25 |
其实这次作业写的代码挺少的,但是功能也很有限
仅仅实现了最基础的展开,合并也是在所有展开做完之后进行的。所以算个\((x-x)**1000\)都得算半天
真是愚蠢的代码!
UML图
尝试用IDEA生成了个uml图,**(脏话)这是啥?太丑了吧!其实这就表明我在HW1的架构特别烂
这是手画的UML图:
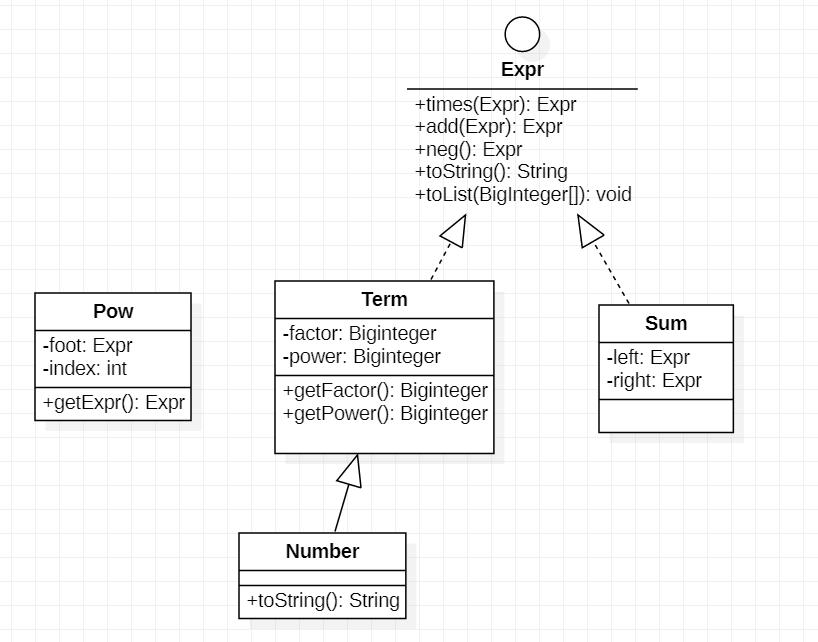
在这次作业中,我用来组织数据的对象只有Term(多项式的项),Sum(项的和),Number(Term的子类),乘法、乘方运算都被我处理成了类的方法,一边解析一边处理
可改进的地方:
- 从这个UML图可以看出来,这个叫Pow的类被晾在了一边,其实这个玩意只是封装了一个我用来展开指数括号的方法,完全没必要作为一个类。把这个方法放在Term类里面更合适
- Main类太杂乱。由于缺乏经验与审美,我把一堆用来解析表达式的方法都塞进了Main里面。这块应该单独整一个Parser类,把获取输入和解析输入分离。
HW2
在HW2中就改进了很多问题(基本上等于Remake)
- 在研讨课之后改了自己混乱的架构,对常规的思路进行了模仿
- 代码写的更像代码了
代码规模
| 类的名称 | 属性个数 | 方法个数 | 行数 |
|---|---|---|---|
| middle.Function | 3 | 2 | 57 |
| middle.Parser | 1 | 8 | 216 |
| middle.Pow | 3 | 3 | 34 |
| middle.Sum | 1 | 2 | 27 |
| organize.factor.Number | 1 | 6 | 40 |
| organize.factor.PowerFactor | 2 | 5 | 43 |
| organize.factor.SinOrCos | 3 | 8 | 65 |
| organize.Expr | 1 | 7 | 117 |
| organize.Term | 2 | 9 | 141 |
| Main | 0 | 2 | 34 |
这么一整,明显感觉程序清晰多了(起码拿给别人看的时候不觉得丢人
UML图
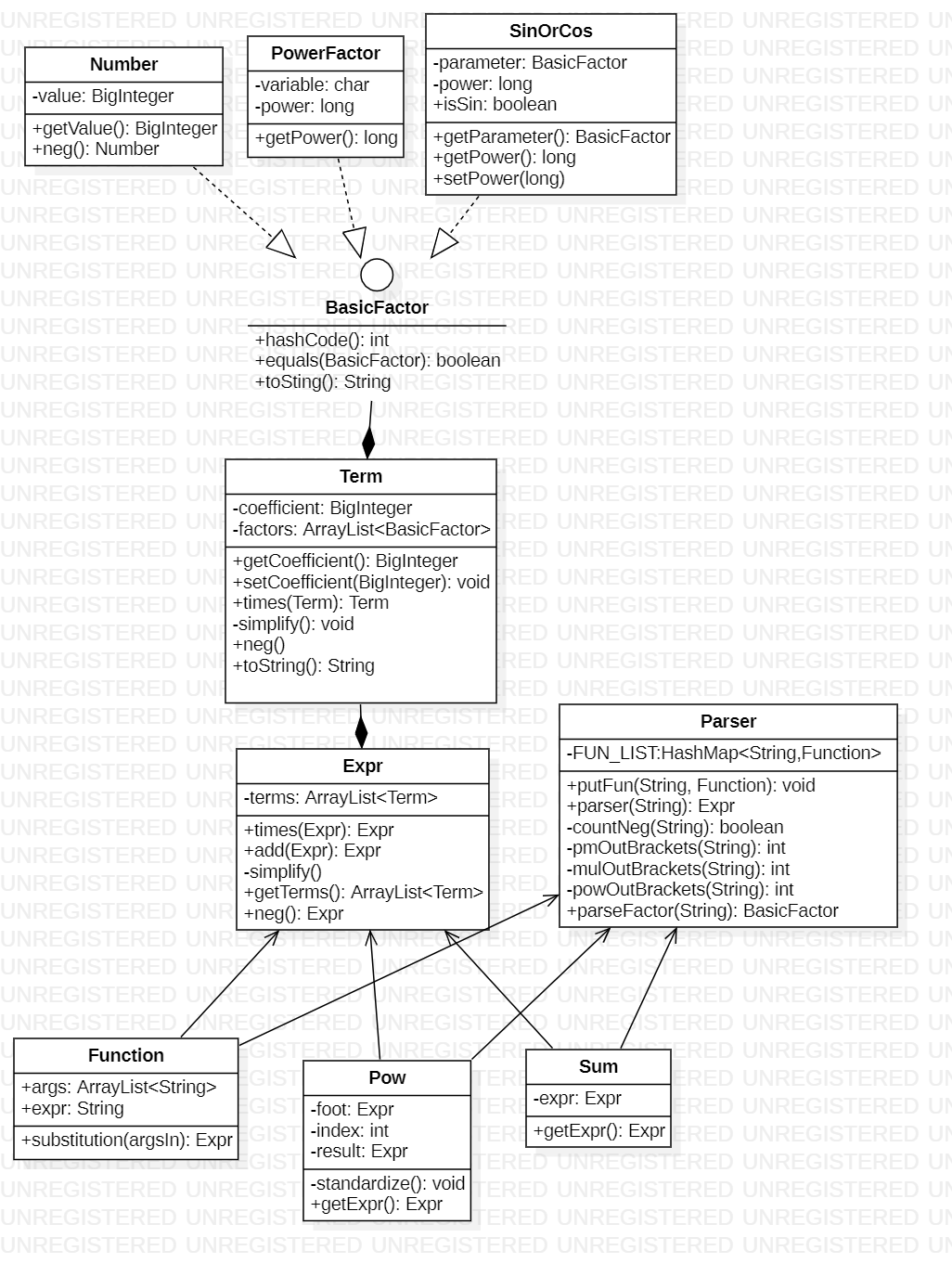
不算很丑:):)
整体分为解析、数据组织、计算及函数处理这三部分。
-
解析采用递归下降的方法
-
数据组织模仿常规的做法,主要分为两个层次Expr和Term,用ArrayList存放数据
-
自定义函数以及Sum函数的处理采用了比较偷懒的字符串替换方法,然后再放进Parser进行解析得到Expr,恕我能力有限
这是整个项目的结构:
src
├── NormalMain.java//主函数
├── middle//用于进行中间过程的计算
│ ├── Function.java
│ ├── Parser.java
│ ├── Pow.java
│ └── Sum.java
└── organize//数据的组织
├── Expr.java
├── Term.java
└── factor//因子
├── BasicFactor.java//这是一个接口
├── PowerFactor.java
└── SinOrCos.java
HW3
代码规模
| 类的名称 | 属性个数 | 方法个数 | 行数 |
|---|---|---|---|
| middle.Function | 3 | 2 | 76 |
| middle.Parser | 1 | 7 | 197 |
| middle.Pow | 3 | 3 | 34 |
| middle.Sum | 1 | 2 | 27 |
| organize.factor.Number | 1 | 6 | 40 |
| organize.factor.PowerFactor | 2 | 5 | 49 |
| organize.factor.SinOrCos | 3 | 8 | 76 |
| organize.Expr | 1 | 7 | 162 |
| organize.Term | 2 | 9 | 148 |
| Main | 0 | 2 | 33 |
圈复杂度分析
可以看出来,parser方法圈复杂度非常高,另外还有Term的Simplify方法,而Term的Simplify也正是我出bug的地方之一。
总体上来看,圈复杂度相当高的地方还不少,我应该之后写代码的时候多注意控制,尽量减少方法之间的耦合,增加代码的可维护性。
(由于原表太长,我删掉了一些不重要的行)
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| middle.Function.Function(String) | 3.0 | 2.0 | 3.0 | 4.0 |
| middle.Function.substitution(String) | 10.0 | 1.0 | 9.0 | 9.0 |
| middle.Parser.countNeg(String) | 4.0 | 4.0 | 3.0 | 4.0 |
| middle.Parser.mulOutBrackets(String) | 8.0 | 3.0 | 6.0 | 9.0 |
| middle.Parser.parse2(String) | 15.0 | 10.0 | 9.0 | 11.0 |
| middle.Parser.parser(String) | 29.0 | 8.0 | 9.0 | 11.0 |
| middle.Parser.pmOutBrackets(String) | 13.0 | 3.0 | 8.0 | 11.0 |
| middle.Parser.powOutBrackets(String) | 8.0 | 3.0 | 5.0 | 8.0 |
| middle.Parser.putFun(String, Function) | 0.0 | 1.0 | 1.0 | 1.0 |
| middle.Pow.getExpr() | 0.0 | 1.0 | 1.0 | 1.0 |
| middle.Pow.Pow(Expr, int) | 0.0 | 1.0 | 1.0 | 1.0 |
| …… | …… | …… | …… | …… |
| organize.Expr.Expr(BasicFactor) | 0.0 | 1.0 | 1.0 | 1.0 |
| organize.Expr.Expr(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| organize.Expr.Expr(char) | 1.0 | 1.0 | 2.0 | 2.0 |
| organize.factor.SinOrCos.copy() | 0.0 | 1.0 | 1.0 | 1.0 |
| organize.factor.SinOrCos.equals(Object) | 4.0 | 3.0 | 4.0 | 6.0 |
| organize.Term.neg() | 0.0 | 1.0 | 1.0 | 1.0 |
| organize.Term.setCoefficient(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| organize.Term.simplify() | 22.0 | 2.0 | 9.0 | 10.0 |
| organize.Term.Term(BasicFactor) | 0.0 | 1.0 | 1.0 | 1.0 |
| organize.Term.Term(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| organize.Term.Term(BigInteger, ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| organize.Term.Term(char) | 0.0 | 1.0 | 1.0 | 1.0 |
| organize.Term.times(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| organize.Term.toString() | 2.0 | 2.0 | 2.0 | 2.0 |
| organize.Term.toStringNoSign() | 5.0 | 2.0 | 3.0 | 5.0 |
| Total | 178.0 | 107.0 | 144.0 | 182.0 |
| Average | 2.966666666666667 | 1.7833333333333334 | 2.4 | 3.033333333333333 |
UML图
hw3真的和hw2没什么区别,UML如下,加了一根线而已
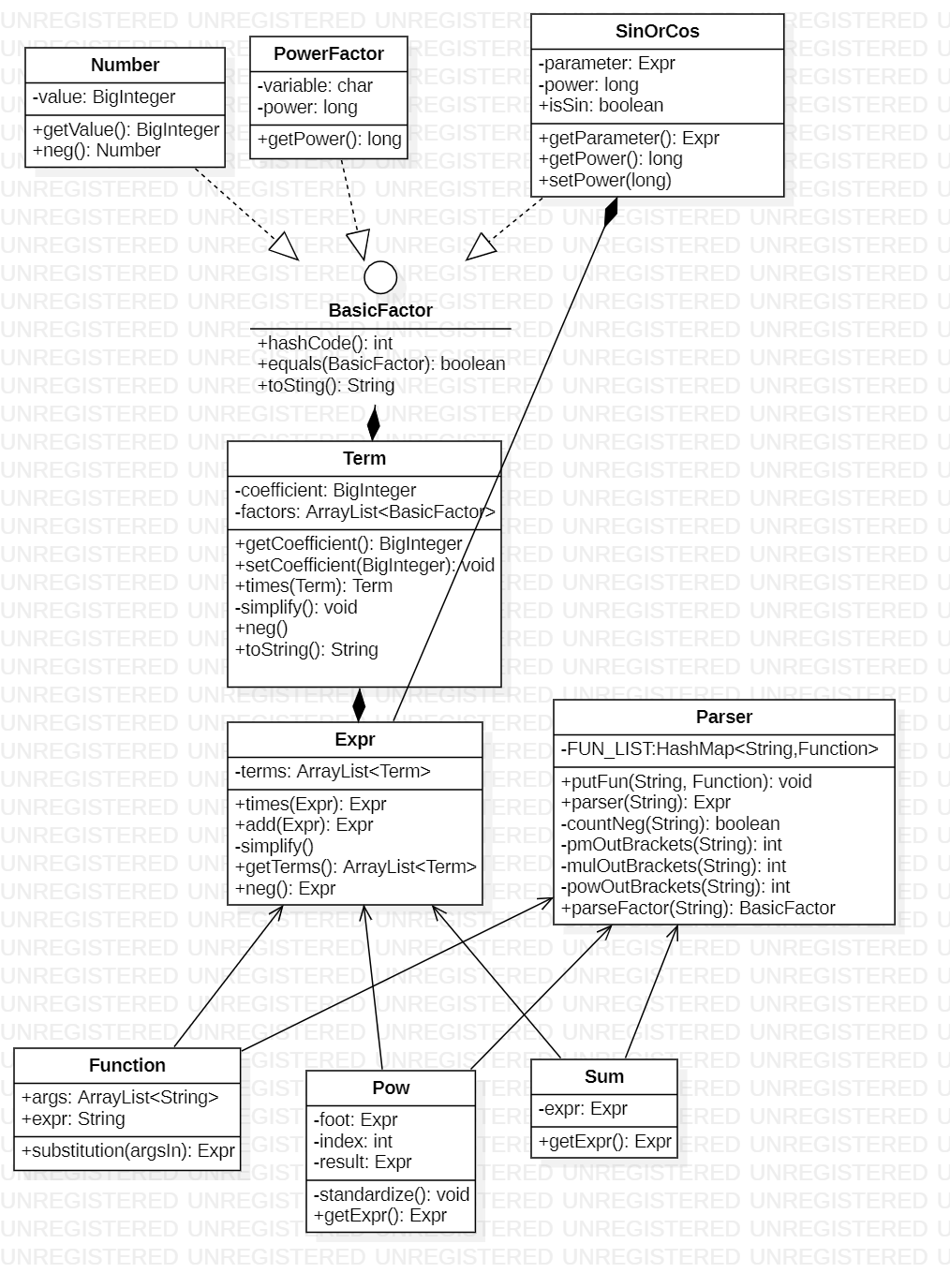
关于化简
我自认为这三次作业中化简做的都不是很好。第一次作业本来有能力化简,却没有意识到化简的重要性。第二三次作业仅仅做了最普通的优化,有这么几点:
- sin(0)=0,cos(0)=1
- 将三角函数内部的东西正负号统一
比如同时出现了sin(x+1)和sin(-1-x),我会将他们都化为sin(x+1),这样输出更短并且让合并同类项合并的更干净 - (Expr)**0 = 1
我只做了这简单的几种化简,甚至没有化简掉平方和公式,其实是因为这个过程中我把问题想的太复杂了,导致无从下手。
比如利用平方和公式化简既要考虑\(sin^2 +cos^2=1\),又要考虑\(1-sin^2 = cos^2\)……我不会简化问题,导致这件事没有做好。-->不要贪多
其实如果仅仅寻找表达式中的 \(Expr1 * sin^2 + Expr1 * cos^2\)这种形式,然后化简为\(Expr1\),就能在强侧中拿到比较好的分数了,但是......我没做这件事。现在想起来有一点点后悔。
Bug及测试
自己的bug
第一次没被hack。
第二次由于粗心(并且测试数据不完备)导致把sin(0)化简为了1,直到交上去都没有发现。
第三次bug有点多
- 首先是sum求和上下界我用的是long,碰到较大的数据就不行了-->
举一反三 - sum求和使用字符串替换处理,负数要加括号-->
仍然要举一反三 - 另一个bug完全是由于我最后临提交做了一点改动导致输出逻辑出了点问题还没做测试-->
任何时候都要测试,不要盲目自信
从这几次作业中获得的小小经验在下面说吧。
hack策略
hack别人本质上也就是测试,那就对拍呗,写个脚本,跑起来
表达式化简正确性的判定可以代入几个x判断。
关键点在于数据的生成。(见下文)
测试经验
-
保存数据,回归测试
不要小瞧一些很简单的数据(其实出错的往往是一些简单的数据)
把自己和别人有过问题的数据都保存起来,每次改版都重新做测试。
-
构造边界数据
数据生成器脚本生成的数据的特点是随机,随机就意味着不能百分之百覆盖到所有可能的类型,手动构造更有目的性,杀伤力更强。
-
关注随机生成数据的“完备性”,而不只是盲目测很多次
心得体会
HW1-闭门造车
闭门造车就是赌
习惯于写完作业再去对答案,还是目光过于狭隘。思维被限制在“最正确的答案只有一个”里面,难以出来。
这是有骨气还是目光短浅呢?
语文不好,表达不尽意思,最后只剩下一句:“博采众长”是褒义词
HW2-"抄作业"
在研讨课上听到别人的思路,感觉真清晰,拿来用了。
HW3-感觉还行
在做HW2的时候比较关注可拓展性,又因为作业三相比2变化不大,很快就写完了。
总体评价
其实要我评价我的这三次作业,答案是:都不满意。
其实作业三交上去的代码有不少地方我还想重构一次
最主要的一点是Term和Expr的组织:
我觉得用HashMap存放Term中的因子和Expr里面的Term更合适
BasicFactor不要包含次数的信息,想三角函数这种就只保存sin()括号里面的东西
Term不要关注coefficient(常系数),仅仅保存幂函数、三角函数,其中的项保存为
HashMap<BasicFactor,Integer> factors;//Integerr是次数Expr用一个HashMap保存Term和其前面的常系数的关系
HashMap<Term,Integer> terms;这样处理起来就更方便(起码比原来会好一些
其实用HashMap存放这个在自然不过了,而我,虽然早就想到了,但是一方面由于定势思维,一方面又由于写好了懒得改,到最后还是用ArrayList修修补补,而在化简的时候却又用了一个中间的HashMap,这种行为很多余,很浪费。
另一点是自定义函数和Sum函数的处理,我是用的字符串替换,但这实在是无计之策,一点也不优美,而且一旦函数定义可以递归或者嵌套,或者sum函数可以包含sum函数,我就寄了。
其实对于总体的架构我还是不太满意,就是在数据的组织方面,但是自己又想不出来更好的。为什么一定要分为Expr和Term两个层次呢?这两个层次明明是同构的,可不可以用一个东西把这两个统一起来又让它便于化简呢?
其实这里我考虑的是可拓展性,如果我们要加入更高层次的东西(我没想出好的例子,希望你能理解我的意思)比如向量,向量的每一项如果都是一个Expr,那按照现在的架构,这一层的东西就得完全重写了。
有没有可能把Expr和Term这两个东西抽象成同一个父类呢?似乎也不是很难,不过很多东西都要重新设计了。
说点好的:我觉得第一单元我的进步挺大。
感谢一路上帮助过我的朋友们,以及,第二单元加油鸭!
❤️❤️❤️



