算法——分而治之,分治法
一、前言
二、分治法
2.1 何为分而治之
2.2 分治法示例
2.2.1 分田
2.2.2 数组求和
三、快速排序
四、总结
五、参考文献
本文将要介绍一种重要的算法解题思路——分而治之,一种著名的递归式问题解决方法。并将使用分而治之的思路实现一个排序算法——快速排序。我们需要注意的是,分而治之不是一种解决问题的具体算法,他是一种思路!
当我们遇到的问题规模较大,较为复杂的时候,我们能否将原问题进行拆解,拆解为几部分,一部分问题的性质和原问题类似,另一部分问题我们能够解决,如果不能解决,就继续进行拆解,直到能解决为止。
分治法思路:
(1)找出基线条件,这种条件必须尽可能简单。
(2)不断将问题分解,缩小问题规模,直到满足符合基线条件为止。
假设你是农场主,有一小块土地,如下图所示:

你要将这块地均匀分成方块,且分出的方块要尽可能大,如下图所示:

需要防止划分分块时出现已经情况:
(1)分出来的不是方块;
(2)方块分得过小;
(3)方块的大小不同;
我们如何采用分而治之的思想来解这道题呢?
(1)找出基线条件,这种条件必须尽可能简单。
我们观察这个田地的长宽发现,如果这个田的长为128,宽为64就好了,这样我们就能很容易的解出题目。如下图所示,直接分成两块64 * 64的方块。
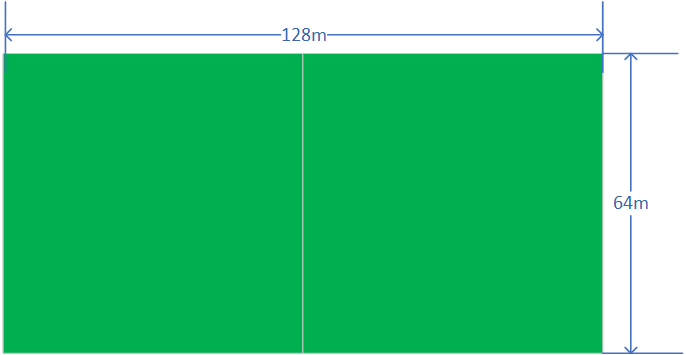
因为,我们推出基线条件为田地的一条边长度为另一条边的整数倍。这种情况是较为简单的,我们容易处理的情况。
(2)不断将问题分解,缩小问题规模,直到满足符合基线条件为止。
我们接下来必须将问题规模进行缩小,在这道题目中,当我们先尝试划分一下,如下图所示:
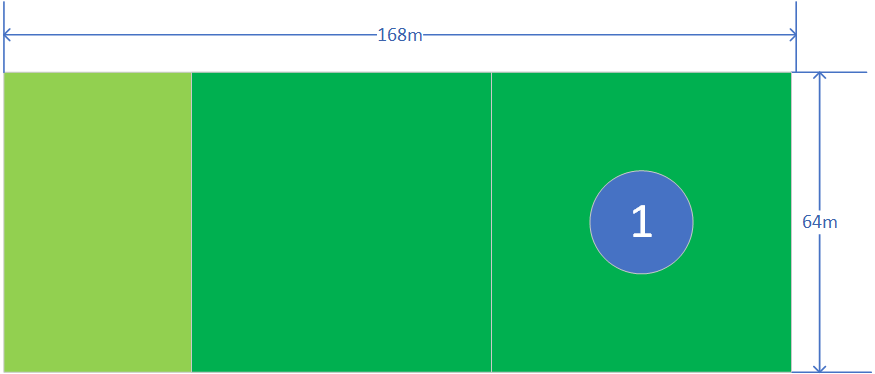
我们划分了两块64*64的方块,还余下一块方块,大小为40*64。那么我们可不可以将余下的这个方块也按照上面的方法进行范围缩小呢?答案是可以的,步骤如下:
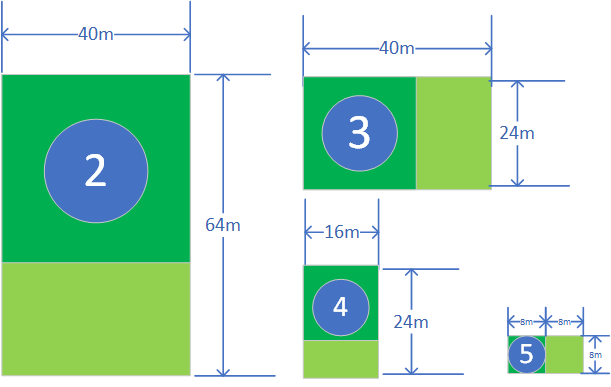
我们最后发现第5步的时候,方块的边长已经满足了基线条件,那么我们就成功找到了满足条件的最大方块。
所以最后的答案就是将这块田地按照8*8的方块进行分田。
假设有一个数组[1, 2, 3, 4],求它的和。
(1)找出基线条件
我们知道,当数组为空,或者只有一个元素时,那么我们能够很容易求出他的和,比如数组[1]的和为1, 数组[2]的和为2。我们找到了基线条件。
(2)缩小问题规模
[1, 2, 3, 4]数组问题规模太大了,怎么缩小呢,我们可以看成1 + [2, 3, 4],而[2, 3, 4]的和又可以看成2 + [3, 4],依次类推。
假设有一数组[10, 5, 2, 3],需要从小到大排序,排序结果为[2, 3, 5, 10],该如何进行排序呢?

(1)找出基线条件
当数组为空,或者只有一个元素的时候,我们很容易进行排序,[1]排序后还是[1],[2]排序后还是[2]。
(2)缩小问题规模
我们可以将数组分为三部分,一部分是基准值,一部分是小于基准值的区,一部分是大于基准值的区。

我们只需要将小于区 + base + 大于区,(小于区,大于区有序),这样我们便完成了缩小问题规模。
实现代码:
1 std::vector<int> quickSort(std::vector<int> arrays) 2 { 3 if (arrays.size() < 2) 4 { 5 return arrays; 6 } 7 else 8 { 9 int base = arrays[0]; // 基准值 10 std::vector<int> less; // 小于基准值分区 11 std::vector<int> greator; // 大于基准值分区 12 for (int i = 1; i < arrays.size(); ++i) 13 { 14 if (arrays[i] < base) 15 { 16 less.push_back(arrays[i]); 17 } 18 19 if (arrays[i] >= base) 20 { 21 greator.push_back(arrays[i]); 22 } 23 } 24 25 less = quickSort(less); // 小于区递归进行排序 26 greator = quickSort(greator); // 大于区递归进行排序 27 28 // 合并小于区,基准值,大于区 29 std::vector<int> result; 30 for (int i = 0; i < less.size(); ++i) 31 { 32 result.push_back(less[i]); 33 } 34 result.push_back(base); 35 for (int i = 0; i < greator.size(); ++i) 36 { 37 result.push_back(greator[i]); 38 } 39 40 return result; 41 } 42 }
当数据量过大时,该解法可能存在爆栈的风险。
分而治之的思路就是找到问题的基准值,即找到问题的一种特殊情况的解法,然后将问题的规模进行缩小,最后利用递归解之。
1、算法图解 作者: [美] Aditya Bhargava 译者:袁国忠





