面向对象程序设计第三单元总结（规格系列）

2019面向对象程序设计第三单元总结

---

前言

---

​ 本单元是规格类作业，和之前的单元相比，本单元作业没有要求我们自己按照自己的想法实现一个工程，而是根据规格进行“契约式”设计，满足所给的需求。在规格方面，作业中使用了JML语言，和以前单纯地指导书中所给的自然语言式的要求相比，这种描述更加全面地描述了一个方法应该以一种什么样的方式来执行，也给出了调用者和编写者的权利与义务，最重要的一点是，这种语言没有二义性，统一了思路，强化了“契约式设计“的概念，这对于团队合作编写一个工程是有及其重要的意义的。另一方面，根据给出的JML的表达式，我们可以很方便地对我们所写的方法进行测试，降低了逻辑错误的发生率，虽然JML在商业方面的用途并不广泛，但是并不代表JML就没有用处。这种规格设计的思想还是让我有很大的收获的。

1.JML语言的理论基础及其工具链

---

理论基础

​ JML(java modeling language)，是一种行为规范语言，遵循契约式设计，重在对规格的定义而并不在实现，目的即避免自然语言的二义性，使得每个java模块都能有严格、唯一的定义。

​ 官网对它的描述为：JML是Java模块的行为接口规范语言。JML提供来规范地描述Java模块的行为，防止模块设计者的意图模糊。JML继承了Eiffel,Larch,Refinement Calculus的思想，其目标是提供严格的形式语义，同时仍然可供任何Java程序员访问。有各种工具可以使用JML的行为规范。由于规范可以作为Java程序文件中的注释编写，或者存储在单独的规范文件中，因此可以使用任何Java编译器编译具有JML规范的Java模块。

​ 语法方面，JML有它自身的语法表达式，在基于JAVA语法基础上，新增了一些操作符和和原子表达式组成的，例如原子表达式：/result 、量化表达式 /forall、集合表达式、操作符:<（表示是子类）等。

​ 规格方面，主要包括：

• 前置条件(pre-condition)
• 后置条件(post-condition)
• 副作用范围限定(side-effects)

​ 因为有了这三个方面，一个方法的行为基本上就固定了，前置条件代表了方法调用者需要满足的义务，后置条件则是方法编写者需要满足的义务，而副作用范围则规定了方法对于一些属性的影响，通过这种权利与义务的制约，调用者和编写者实际上也就形成了一种契约，使得方法的编写和使用有了严格的限制，这种规格和契约的思想，在某种程度上也会减少bug的产生，并且也方便了测试，遗憾的是，JML语言在复杂场景的表现似乎并不出色，在第三次作业中我们可以看到，接口中多出了好多中间方法，但这并不代表JML就不出色，JML出色的地方其实是它的思想，这种不同于自然语言，没有二义性的语言，对于合作实现一个需求是有很大帮助的。

工具链

• OpenJML：可以对代码进行JML规格的语法的静态检查，还支持使用SMT Solver动态地检查代码对JML规格满足的情况，因此OpenJML一般也自带有其支持的JML solver。

• JML UnitNG：根据JML描述自动生成与之符合的测试样例，重点会检测边界条件。

  工具上来说其实挺少的，因为在接触JML的时候我们其实可以看到IDEA对JML也没有相关的开发工具，还需要我们手动修改插件或者使用命令行来使用OpenJML。

2.JMLUnitNG的使用

---

​ 本部分参考的基本上是讨论区帖子的方法。

• 首先需要安装好OpenJML与jmlunitng.jar，然后将我们编写的文件放于demo这个package（文件夹）中：

• Demo.java: 由于不能使用/forall等，因此只保留了几个简单的pure方法

  package demo;
  
  import java.util.ArrayList;
  
  public class Demo{
      public ArrayList<Integer> nodeList = new ArrayList<Integer>();
  
      // @ public normal_behaviour
      // @ ensures \result = nodeList.size();
      public  /*@pure@*/ int size() {
          return nodeList.size();
      }
      
      // @ public normal_behaviour
      // @ requires index >= 0 && index < size();
      // @ assignable \nothing;
      // @ ensures \result == nodeList.get(index);
      public /*@pure@*/ int getNode(int index) { 
          if (index < 0 || index >= size()) {
              return -1;
          }
          return nodeList.get(index);
      }
  
      // @ public normal_behaviour
      // @ ensures \result = nodeList.size() >= 2;      
      public /*@pure@*/ boolean isValid() {
          return nodeList.size() >= 2;
      }
  
  public static void main(String[] args) {
          Demo demo1 = new Demo();
          demo1.nodeList.add(1983);
          demo1.nodeList.add(-1983);
          System.out.println(demo1.size());
          System.out.println(demo1.getNode(1));
          System.out.println(demo1.isValid());
      }
  }
  

• 执行命令：

java -jar jmlunitng.jar demo/Demo.java

​ 执行结束后的demo文件夹应该为：

• 编译文件：

  编译部分共分为两步：

  ​ 1.用 javac 编译 JMLUnitNG 的生成文件

  ​ 2.用 jmlc 编译自己的文件，生成带有运行时检查的 class 文件

• 进行测试：

  ​ 执行java -cp jmlunitng.jar demo/Demo_JML_Test

• 执行结果：

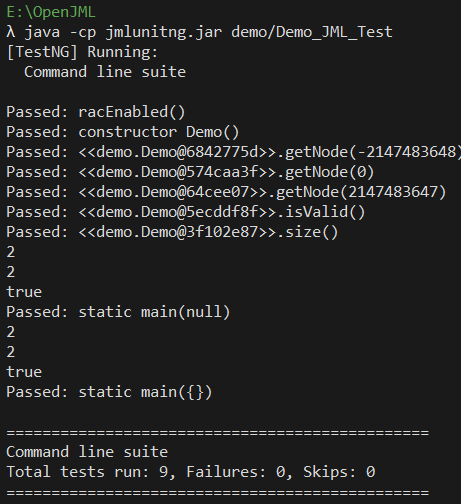
可以看到，JunitNG侧重于对边界条件的测试，这对我们的程序测试是很有帮助的。

3.作业需求分析

---

​ 本单元的的作业需要我们根据接口中所给出的JML规格，在理解方法功能、类功能的基础上，实现对应的类和方法，使之能满足JML规格的定义。在程序运行结果上体现为，对于给定的合法输入，能给出正确的运行结果，并且程序运行的性能不能低于给定的性能下限。

4.作业架构设计

---

4.1 第九次作业

---

作业思路分析：

​ 本次作业看似很简单，但是由于CPU时间的限制，需要我们在执行查询型的方法时要尽量保证复杂度为O(1)，因此，查询复杂度为O(1)的容器有Hashmap，或者在执行PathContainer的结构变更方法时就将某些要查询的值缓存下来，这样在下次查询时直接读取数即可：

​ 相应地，本次作业典型的两个方法为distinctNodeCount()方法：

​ 在Path里，使用Hashset即可,，因为Path的结构不会变更，而且HashSet不会存储重复元素。

    private HashSet<Integer> set = new HashSet<>();

​ 在PathContainer里，使用双容器，Path和id可以互相查询，相应的，需要重写HashCode和equals方法：

private HashMap<Integer, Path> pathContain = new HashMap<>();
private HashMap<Path, Integer> integerContain = new HashMap<>();

​ 并且，保存一个globalPath变量，记录Path中每个node出现的次数：

private HashMap<Integer, Integer> globalPath = new HashMap<>();

若次数为0则删除这个节点，这样返回的size就是distinctNodeCount的值，相应地，对globalPath的改变需要在addPath和removePath里进行，因为要遍历Path，所以要重写迭代器方法。

private void addNode(Path e) {
    for (int i : e) {
        if (globalPath.containsKey(i)) {
            globalPath.put(i, globalPath.get(i) + 1);
        } else {
            globalPath.put(i, 1);
        }
    }
}

private void removeNode(Path e) {
    for (int i : e) {
        if (globalPath.get(i) == 1) {
            globalPath.remove(i);
        } else {
            globalPath.put(i, globalPath.get(i) - 1);
        }
    }
}

类图：

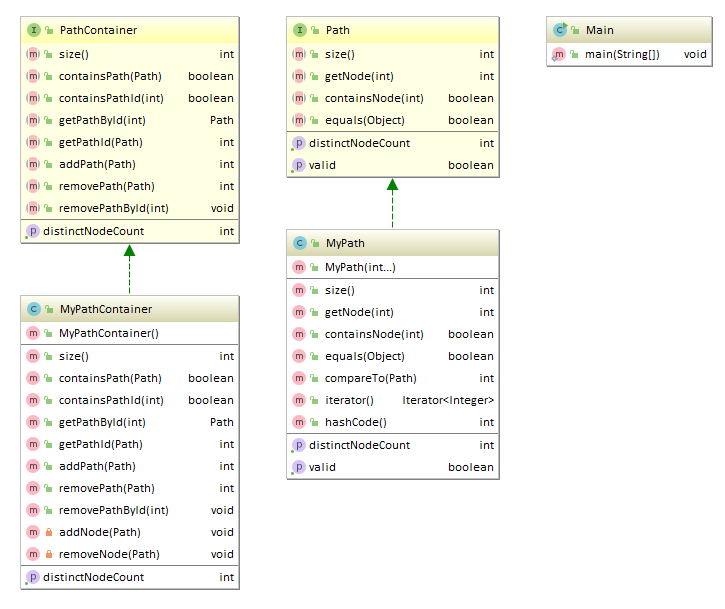
​ 第九次作业的架构较为简单，因为只需实现两个类即可，因此也只需要实现类所对应的方法，addNode和removeNode则是为了globalPath服务的，目的是为了将distinctNodeCount缓存下来，将复杂度分散到出现次数较少的add 和 remove方法里。

4.2 第十次作业

---

作业思路分析：

​ 本次作业相比于第九次作业相比，需要我们从PathContainer中抽象出一个图，并对这个无向图进行一些基本的图相关的计算，考虑到globalPath可以被Graph替代，因此这次我依然只开了两个类：MyGraph和MyPath，实质上MyGraph包含了PathContainer里的所有方法，Graph类似于一个邻接表，保存了一个Node相邻的所有节点，同时也统计节点出现的次数，Graph图结构的变更同样在add 和 Remove中进行：

private HashMap<Integer, HashMap<Integer, Integer>> graph = new HashMap<>();

​ 首先是containsNode方法和containsEdge方法，只需在graph中查询即可。

​ 其次是isConnected和getShortestPathLength方法，isConnected依赖于getShortestPath进行，若距离为无穷远，则显然不连通。

​ 最短路径方法我采用了弗洛伊德算法，在add 和 remove方法执行的时候就重新计算各点的最短路径，因为查询比图变更指令多的多：

private void floyd() {
    for (HashMap.Entry<Integer, HashMap<Integer, Integer>>
            disEntry1 : distance.entrySet()) {
        for (HashMap.Entry<Integer, HashMap<Integer, Integer>>
                disEntry2 : distance.entrySet()) {
            for (HashMap.Entry<Integer, HashMap<Integer, Integer>>
                    disEntry3 : distance.entrySet()) {
                int curKey3 = disEntry3.getKey();
                int dirDis = disEntry2.getValue().get(curKey3);
                int pathDis = disEntry2.getValue().get(disEntry1.getKey())
                        + disEntry1.getValue().get(curKey3);
                if (dirDis > pathDis) {
                    disEntry2.getValue().put(curKey3, pathDis);
                }
            }
        }
    }
}

​ 这里有一个缺点，遍历hashmap的速度太慢，可以更改为静态数组来进行。

​ 这样这四个查询指令就完成了。

类图：

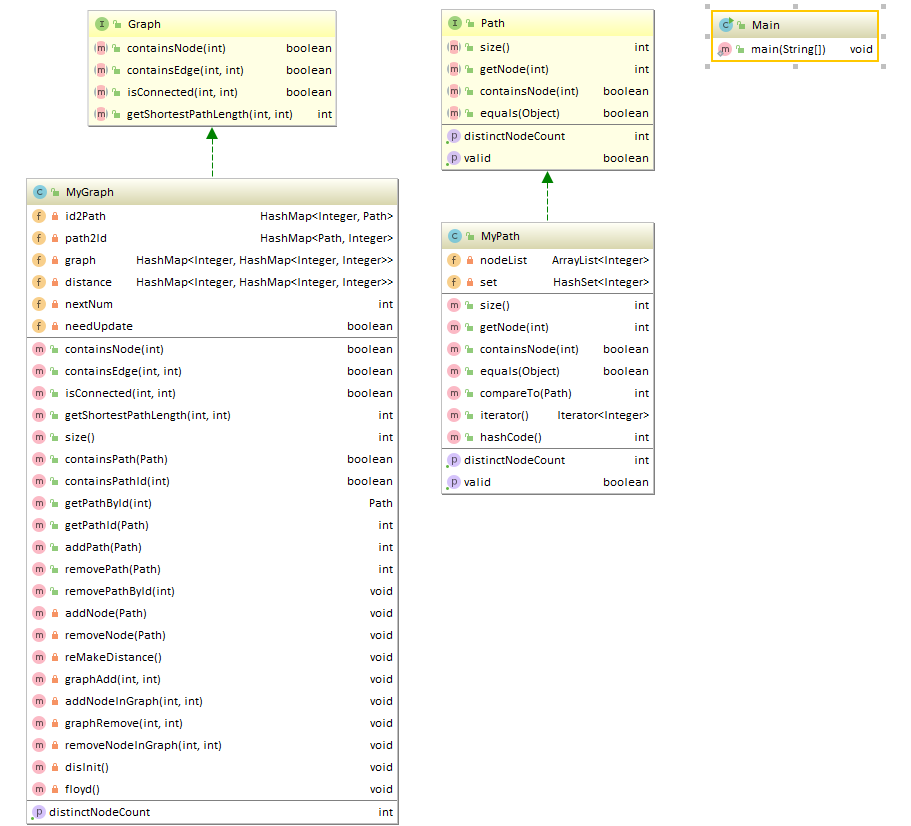
​ 本次作业在上一次作业的基础上，新增了4个查询方法，Path类方法中，没有变化，原来的PathContainer类作为Graph的父类，本应该采用继承的关系，但我为了省下globalPath变更时消耗的额外时间，因为可以被Graph替代，没有从上一次作业中继承Container类，而是复制粘贴了上一次的大部分代码，并且对其一些方法进行了修改，这其实和课程组期望的增加新功能在新的类里增加是有相违背的，其实也就是为了性能牺牲了一部分架构，使得Graph类和PathContainer类杂糅在了一起，在这一点上，我做的并不好，在上一次的作业中没有考虑好架构的可扩展性，让graph这个class变得有点像超级类了。

4.3 第十一次作业

---

作业思路分析：

​ 本次作业和上次相比，将Graph扩展成了地铁线路图，同时新增了5个查询方法，一个是连通块的数量，在这里我使用了并查集实现：

private int find(int x) {
    if (set.get(x) != x) {
        set.put(x, find(set.get(x)));
    }
    return set.get(x);
}

private void join(int x, int y) {
    int fx = find(x);
    int fy = find(y);
    if (fx != fy) {
        set.put(fx, fy);
    }
}

private void getBlockNum() {
    int num = 0;
    for (HashMap.Entry<Integer, Integer> x : set.entrySet()) {
        if (x.getKey().equals(x.getValue())) {
            num++;
        }
    }
    blockNum = num;
}

​ 并查集的好处是，效率较高，只有删除节点时需要重构。

​ 其他四个查询方法，其实和查两点间的最短路差不多，不一样的只是各条边的权重而已，这里我还是用了弗洛伊德算法，并新增了一个类，ShorestPath类，用于计算最短路相关的方法，同时，在上一次作业基础上进行了优化，改成静态数组实现，大大提高了程序的性能。

​ 具体实现为：每个Path使用弗洛伊德算法计算一次各点之间的最短路，然后将它并到最终的地铁网络中，不同Path之间的距离加上不同查询方法所需的权重，再进行一次弗洛伊德算法，就得到了最终的结果，由于只有120个节点，其实算法复杂度并不高。

​ 这里给出leastTicketPrice算法的实现，也特别简单，可见数学和算法的重要性：

private void getPrice() {
    leastPrice = init(2);
    for (Path e : paths.keySet()) {
        int maxLen = e.size();
        int[][] distance = init(2);
        for (int i = 0; i < maxLen - 1; i++) {
            int temp1 = int2int.get(e.getNode(i));
            int temp2 = int2int.get(e.getNode(i + 1));
            distance[temp1][temp2] = 1;
            distance[temp2][temp1] = 1;
        }
        floyd(distance);
        for (int i = 0; i < maxLen - 1; i++) {
            int temp1 = int2int.get(e.getNode(i));
            for (int j = i + 1; j < maxLen; j++) {
                int temp2 = int2int.get(e.getNode(j));
                if (distance[temp1][temp2] + 2 < leastPrice[temp1][temp2]) {
                    leastPrice[temp1][temp2] = distance[temp1][temp2] + 2;
                    leastPrice[temp2][temp1] = distance[temp2][temp1] + 2;
                }
            }
        }
    }
    floyd(leastPrice);
}

​ 需要注意的是，最终的结果会多出一次换乘的代价，需要在计算结果时减去。

​ 同样在add 和 remove中执行路径的重新计算。

类图：

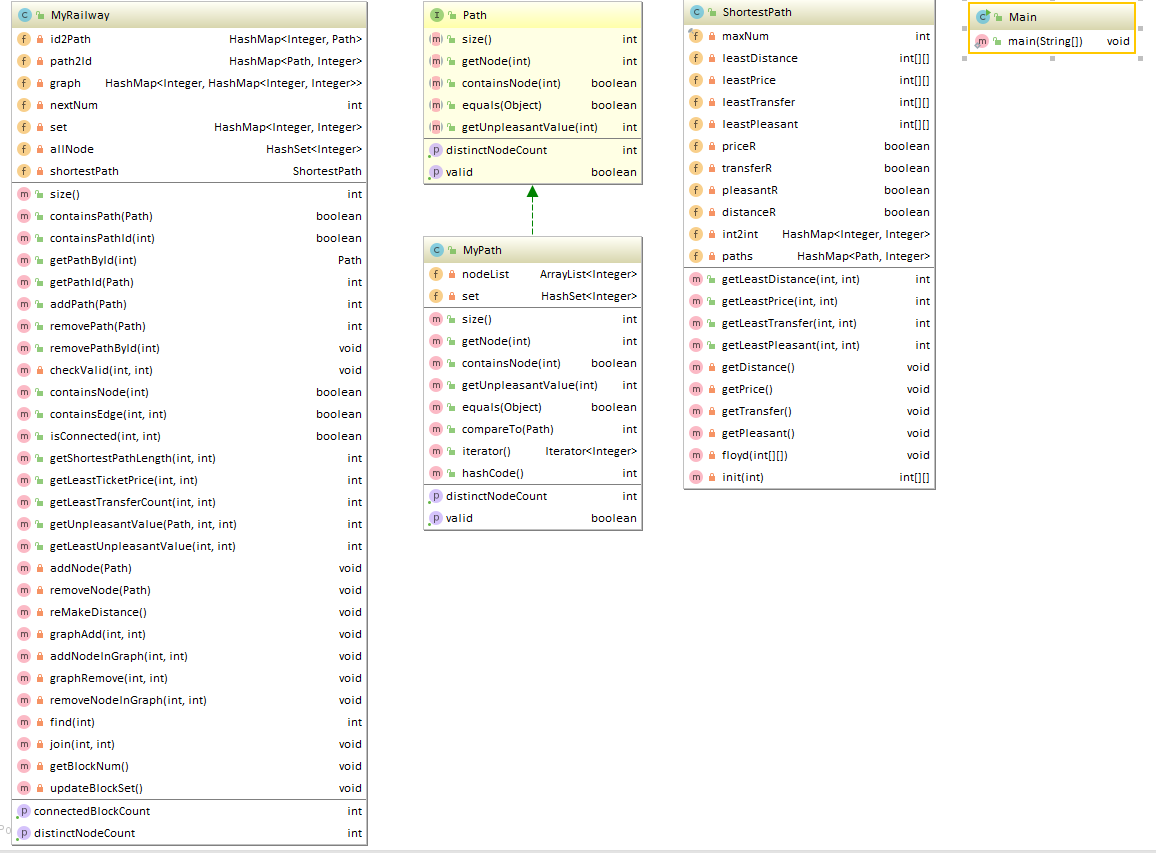
​ 本次作业的架构其实延续了上一次作业的通病，但是这次把和图计算相关的操作都整合到了ShortestPath类中，在更新时只需要new一个ShortestPath对象即可，但是依旧把PathContainer和Graph杂糅在了一起，也就是把和图结构的简单计算都放在了这个类中，ShortestPath类做到了一部分课程组所要求的把图计算相关的单独整合到一个类中，但其实还是挺混乱的，这次作业由于一开始想了好久也不知道怎么写，最后看了讨论区里的帖子才有了启发，一开始的架构就被打乱了，但这次作业对于架构其实也没有重构很多，只是把计算路径的方法都整合到了一个类中，因为这类方法都比较复杂，并且都在add和remove时需要更新，最重要的是都是同一个图，只是权重不一样，因此将它们并到一起我认为还是很合适的，其他图简单计算依旧放到了Graph类中，导致了Graph类比较复杂、混乱，以后在写作业以前还是要多多思考架构方面的问题。

5.bug分析

---

​ 本单元的作业中只有第十次作业出现了CPU时间超时的点，但是在bug修复阶段，我重新提交了一模一样程序，原本CTLE的点却通过了，有点不太明白，因此本部分就简略阐述一下互测发现bug的策略。本单元的作业中正确性方面实现的较好，因此没有出现Wrong Answer类错误。在互测方面，先通过运行程序来实现bug定位，再通过阅读其对于图计算的算法，估计复杂度，判断有无超时的可能，再通过阅读有错误程序的代码来发现具体bug出现的位置，最后查看有没有其他逻辑上的bug，如果有则最终提交bug。

6.本单元心得体会

---

​ 总的来说，在本单元中收获还是很大的，尤其是JML契约式设计的思想，只要满足JML规格就能保证正确性，也让方法的编写者有了一个明确的目标，编写出满足需求的代码，同时也告诉了调用者所应该满足的条件，这种权利义务互相制约，最后让一个方法的调用完美执行的思想，其实是很受用的，在以后有多人合作，而且需要严格保证正确性的工程上，就可以应用JML来实现bug相对较少的工程。但是，我们自己编写规格的时候也能看到，编写规格并不是一件容易的事情，需要在编写时就要把各种情况都考虑到了，编写规格的过程上其实也可以让自己对工程架构有一个整体的理解，此外，编写规格其实比写方法还要更加复杂一些，例如第三次作业的规格我们可以看到，接口里添加了很多中间方法，让规格变得更加复杂了，但逻辑上还是很清晰的，编写规格的复杂性可能也是JML通途不广泛的一个原因吧。OO课程也块走到尾声了，希望自己在最后一个单元中能学到更多的东西，继续加油！