深入学习二叉树（01）完全二叉树

前言

如果二叉树的深度为k，则除第k层外其余所有层节点的度都为2，且叶子节点从左到右依次存在。也即是，将满二叉树的最后一层从左到右依次删除若干节点就得到完全二叉树。

满二叉树是一棵特殊的完全二叉树，但完全二叉树不一定是满二叉树

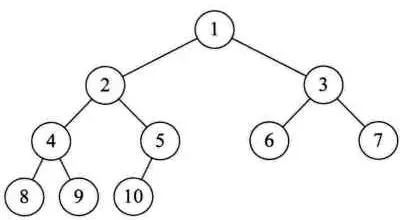
如何实现一棵完全二叉树?

现在给定数组data [3,2,5,8,4,7,6,9] ,使用二叉链表生成完全二叉树

树的节点

typedef struct node{
    int data;
    struct node * left,* right;
}TreeNode;

定义一个 数据域与两个指针域，数据域存储节点数据，指针域指向该节点的左子树与右子树

设计实现

为了方便实现该树，所以数组第一个节点设计为无效节点，从2个数据开始

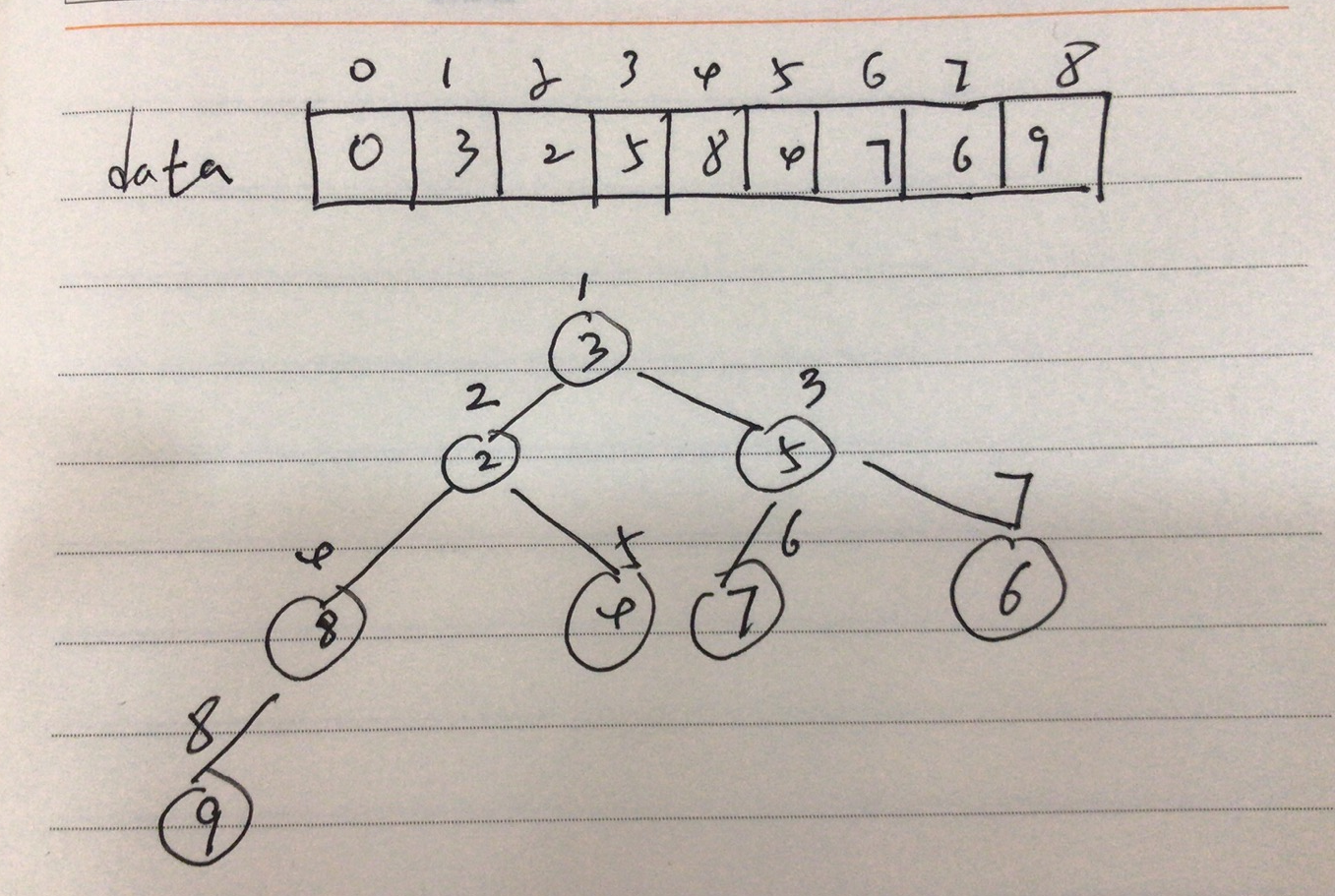
 结果输出

//前序遍历
void print(TreeNode *root){    
    printf("%5d",root->data);
    if(root->left!=NULL){
        print(root->left);
    }
        
    if(root->right!=NULL){
        print(root->right);
    }
}

//中序遍历
void print(TreeNode *root){    
    if(root->left!=NULL){
        print(root->left);
    }
    printf("%5d",root->data);    
    if(root->right!=NULL){
        print(root->right);
    }
}

//后序遍历
void print(TreeNode *root){    
    if(root->left!=NULL){
        print(root->left);
    }
        
    if(root->right!=NULL){
        print(root->right);
    }
        printf("%5d",root->data);
}

实现原理

TreeNode * createTree(int data[],int n,int index){
	TreeNode *root = NULL,*left = NULL,*right = NULL;
	//create LeftTree
	if(index<=n&&index*2<=n){
		left = createTree(data,n,index*2);
	}
	//createRigntTree
	if(index<=n&&index*2+1<=n){
		right = createTree(data,n,index*2+1);
	}
	//createNode
	if(index<=n){
		root = (TreeNode *)malloc(sizeof(TreeNode));
		root->data = data[index];
		root->left = left;
		root->right = right;	
	}
	//return root 
	return root;
}　　

接收一个数组，采用递归的方法将子节点依次生成，最后返回当前的节点。

 完整代码

#include<stdio.h>
#include<stdlib.h>
typedef struct node{
    int data;
    struct node * left,* right;
}TreeNode; 

TreeNode * createTree(int data[],int n,int index){
    TreeNode *root = NULL,*left = NULL,*right = NULL;
    //create LeftTree
    if(index<=n&&index*2<=n){
        left = createTree(data,n,index*2);
    }
    //createRigntTree
    if(index<=n&&index*2+1<=n){
        right = createTree(data,n,index*2+1);
    }
    //createNode
    if(index<=n){
        root = (TreeNode *)malloc(sizeof(TreeNode));
        root->data = data[index];
        root->left = left;
        root->right = right;    
    }
    //return root 
    return root;
}

void print(TreeNode *root){    
    printf("%5d",root->data);
    if(root->left!=NULL){
        print(root->left);
    }
        
    if(root->right!=NULL){
        print(root->right);
    }
}

int main(){
    int data[] ={0,3,2,5,8,4,7,6,9};
    TreeNode * root = createTree(data,8,1);
    printf("begin print ...\n");
    print(root);
    printf("\nend ... print:\n");
    return 0;
}