深入学习二叉树（02）线索二叉树

1.产生背景

现在有一棵节点数目为 n 的二叉树，采用二叉链表的形式存储。对于每个节点均有指向左右孩子的两个指针域。而节点为 n 的二叉树一共有 n-1 条有效分支路径。那么二叉链表中一共

存在2n-(n-1) = n+1 个空指针域。那么这些空指针域造成了空间浪费。

如图：所示一棵二叉树一共有10个节点，空指针有 11 个

 

 

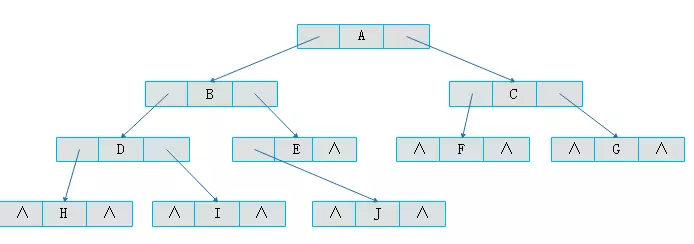
 此外，当对二叉树进行中序遍历时可以得到二叉树的中序列。例如上图中二叉树中序遍历结果为 HDIBJEAFCG ,那么得知 A 的前序节点为 E ，后继节点为 F。但是这种关系的获得是建立在

完成遍历后得到的，那么是否在遍历之前就记录下前驱和后继的关系呢？ 那么在寻找前驱与后继节点时，将大大的提升效率。

2.线索化

现将某节点的空指针域指向该节点的前序后继，定义规则如下

若结点的左子树为空，则该结点的左孩子指针指向其前驱结点。
若结点的右子树为空，则该结点的右孩子指针指向其后继结点。

这种指向前驱和后继的指针称为线索。将一棵普通二叉树以某种次序遍历，并添加线索的过程称为线索化，按规则将上图线索化后如下图

 

 

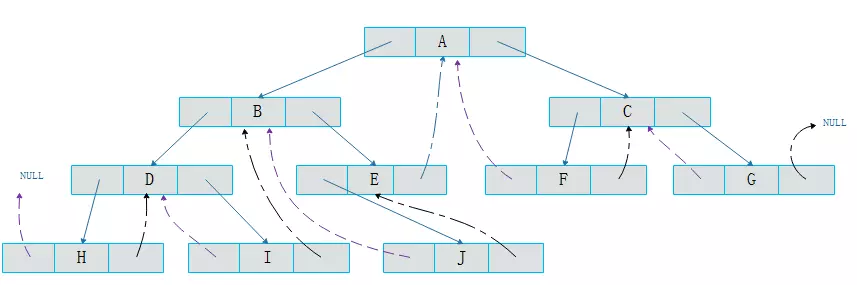
 图中黑色点画线为指向后继的线索，紫色虚线为指向前驱的线索。可以看出通过线索化，即解决了空间浪费的问题，又解决了前驱后继的记录问题。

2.1 线索化带来的问题

经过上述的线索化后，可以将一棵二叉树线索化为一棵线索二叉树，那么新的问题会产生，我们如何区分一个节点的 指针域是指向孩子还是前驱后继节点呢？

为了解决这个问题，现在需要添加标志位 ltag , rtag 并定义规则如下

ltag为0时，指向左孩子，为1时指向前驱
rtag为0时，指向右孩子，为1时指向后继

添加 ltag 和 rtag 属性的节点结构如下

 

 转变为如下的二叉树

 3.实现线索二叉树

3.1 中序线索二叉树

为了方便构建一棵二叉树，这里使用完全二叉树构建线索二叉树，如下图是一棵完全二叉树

 

构建完全二叉树参考：https://www.cnblogs.com/baizhuang/p/11612961.html

接下来需要对此二叉树进行线索化

static TreeNode *pre = NULL;
void initTag(TreeNode *p){
    if(p!=NULL){ 
        initTag(p->lchild); // 递归左子树
        if(p->lchild==NULL){
            p->lchild=pre;
            p->lTag=1;
        } 
        if(pre!=NULL&&pre->rchild==NULL){
            pre->rchild=p;
            pre->rTag=1;
        }
        pre=p;
        initTag(p->rchild);// 递归右子树
    }
}

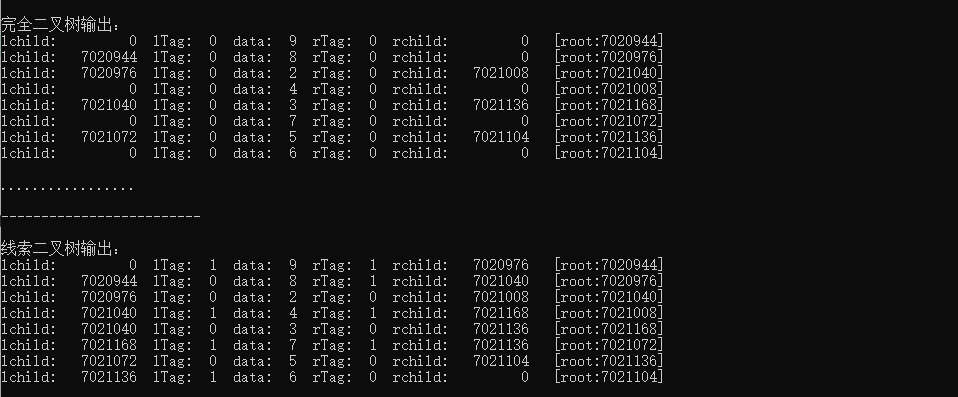
线索化后如下图

 

 方便观察，控制台输出如下

 

 完整代码：

#include<stdio.h>
#include<stdlib.h>
typedef struct node{
	int data;
    struct node * lchild,* rchild;
    int lTag,rTag;
}TreeNode; 

static TreeNode *pre = NULL;

TreeNode * createTree(int data[],int n,int index){
	TreeNode *root = NULL,*lchild = NULL,*rchild = NULL;
	//create lchildTree
	if(index<=n&&index*2<=n){
		lchild = createTree(data,n,index*2);
	}
	//createRigntTree
	if(index<=n&&index*2+1<=n){
		rchild = createTree(data,n,index*2+1);
	}
	//createNode
	if(index<=n){
		root = (TreeNode *)malloc(sizeof(TreeNode));
		root->data = data[index];
		root->lchild = lchild;
		root->rchild = rchild;
		root->lTag = root->rTag = 0;	
	}
	//return root 
	return root;
}

void print(TreeNode *root){	
	if(root->lchild!=NULL){
		print(root->lchild);
	}
    printf("lchild:%10d  lTag:%3d  data:%3d  rTag:%3d  rchild:%10d   [root:%d]\n",root->lchild,root->lTag,root->data,root->rTag,root->rchild,root);
	if(root->rchild!=NULL){
		print(root->rchild);
	}
}

void printSearchTree(TreeNode *root){
	if(root!=NULL){
	 if(root->lTag==0){
	 	printSearchTree(root->lchild);
	 }
	printf("lchild:%10d  lTag:%3d  data:%3d  rTag:%3d  rchild:%10d   [root:%d]\n",root->lchild,root->lTag,root->data,root->rTag,root->rchild,root);
	// printf("%d",root->lTag);
	 if(root->rTag==0){
	 	printSearchTree(root->rchild);
	 }
	}
}


void initTag(TreeNode *p){
    if(p!=NULL){ 
        initTag(p->lchild); // 递归左子树
        if(p->lchild==NULL){
            p->lchild=pre;
            p->lTag=1;
        } 
        if(pre!=NULL&&pre->rchild==NULL){
            pre->rchild=p;
            pre->rTag=1;
        }
        pre=p;
        initTag(p->rchild);// 递归右子树
    }
}


int main(){
	int data[] ={0,3,2,5,8,4,7,6,9};
	TreeNode * root = createTree(data,8,1);
	printf("\n完全二叉树输出：\n");
	print(root);
	printf("\n.................\n");
	
	initTag(root); 
	printf("\n-------------------------\n");
	printf("\n线索二叉树输出：\n");
	printSearchTree(root);
	printf("\n-------------------------\n");
	return 0;
} 

　参考：https://www.jianshu.com/p/3965a6e424f5