复杂网络分析-个人笔记 总结

一. 工具

1. Python 3.7

2. NetworkX 2.3

这是一个专门用于复杂网络分析的包，执行pip install networkx即可安装。

二、网络基本性质

1. 节点数

网络中包含的节点个数。

2. 连接数

网络中包含的边的个数。

3. 密度

网络中包含的边的个数占网络中所有可能的边的个数的比例。

4. 聚集系数

也称为局部聚集系数，是网络中每个节点的聚集系数的平均值。节点的聚集系数为，将该节点的所有邻居两两组合，则共有C^2_{d_v}种组合，组合中的两个节点为邻居的组合数占所有组合数的比例即为该节点的聚集系数。

5. 传递性

也称为全局聚集系数，即网络中的三角形结构占所有可能的三角形结构的比例。

6. 互惠性

互惠性是有向图的性质，即在有向图中，双向连接的边占所有边的比例。

三、中心性分析

中心性分析包括两方面，分别是节点的中心度和整体网络的中心势。

1. 点度中心性（degree centrality）

在无向网络中，我们可以用一个节点的度数（相当于你的微信好友数）来衡量中心性。在微博中，谢娜的粉丝数9千多万，她的点度中心性就很高。

这一指标背后的假设是：重要的节点就是拥有许多连接的节点。你的社会关系越多，你的影响力就越强。

 

 

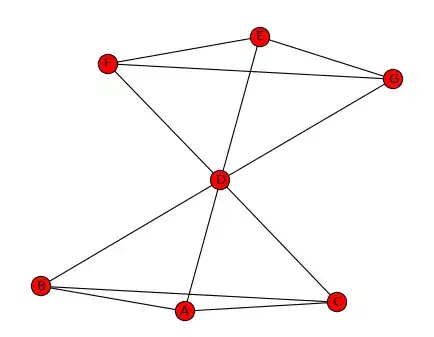
图1：使用networkx绘制的蝴蝶结网络

 

在上面的蝴蝶结网络中，节点D的连接数是6，和网络中的所有人都建立了直接联系，其他节点的连接数都是3，因此节点D的点度中心性最高。整个网络一共有7个节点，意味着每个人最多可以有6个社会关系。因此，节点D的点度中心性是6/6=1，其他节点的点度中心性是3/6=0.5。

 

1. 节点中心度

节点中心度包括三种，分别为度数中心度、接近中心度和中介中心度。

（1）度数中心度（degree centrality）

 

度数中心度是与某节点直接相连的其他节点的个数，如果一个点与许多点直接相连，那么该点具有较高的度数中心度。在有向图中，度数中心度分为出度中心度和入度中心度。由于这种测量仅关注与某一个节点直接相连的点数，忽略间接相连的点数，因此被视为局部中心度。

（2）接近中心度（closeness centrality）

接近中心度是某个节点与图中所有其他点的最短距离之和的倒数，一个点越是与其他点接近，该点在传递信息方面就越不依赖其他节点，则该点就具有较高的接近中心度。在有向图中，接近中心度分为出接近中心度和入接近中心度。

（3）中介中心度（betweenness centrality）

中介中心度测量了某个节点在多大程度上能够成为“中间人”，即在多大程度上控制他人。如果一个节点处于多个节点之间，则可以认为该节点起到重要的“中介”作用，处于该位置的人可以控制信息的传递而影响群体。

（4）绝对中心度和相对中心度

上面描述的三种中心度的计算方法都是绝对中心度，绝对中心度有一个缺陷是，对于不同结构和规模的网络中的节点，其中心度无法直接进行比较，因此提出了相对中心度。相对中心度可以理解为是对绝对中心度进行了标准化。相对中心度的计算公式如下：

  • 度数中心度：
    C_{deg}(v)=\frac{d_v}{|N|-1}
    d_v是节点v的邻居数量，N是网络中的所有节点的集合，|N|是网络中节点的个数。

  • 接近中心度：
    C_{close}(v)=\frac{|R(v)|}{|N|-1}\frac{1}{\sum_{u\in{R(v)}}d(u,v)}
    R(v)是所有从节点v出发可达的节点集合，d(u,v)为节点u和节点v之间的最短距离。

  • 中介中心度：
    C_{btw}(v)=\sum_{s,t\in{N}}\frac{\sigma_{s,t}(v)}{\sigma_{s,t}}
    \sigma_{s,t}是节点s与节点t之间最短路径的条数，\sigma_{s,t}(v)是节点s与节点t之间经过节点v的最短路径的条数。

2. 网络中心势

整体网络的中心势与节点的中心度相对应，也有三种，分别为度数中心势、接近中心势和中介中心势。

（1）度数中心势（degree centralization）

C_D=\frac{\sum_{v\in N}max(C_{dge})-C_{dge}(v)}{|N|-2}

（2）接近中心势（closeness centralization）

C_C=\frac{\sum_{v\in N}max(C_{close})-C_{close}(v)}{(|N|-1)(|N|-2)/(2|N|-3)}

（3）中介中心势（betweenness centralization）

C_B=\frac{\sum_{v\in N}max(C_{btw})-C_{btw}(v)}{|N|-1}

四、利用NetworkX来进行社会网络分析

1. 构建网络

在networkx中定义了许多种网络，例如无向图、有向图、二分图、多层网络等等，这里我们使用有向图来做分析。

import networkx as nx
G = nx.DiGraph() #初始化一个有向图
G.add_edge('A', 'B') #添加边
G.add_edge('A', 'D')
G.add_edge('B', 'C')
G.add_edge('B', 'D')
G.add_edge('D', 'E')
G.add_edge('E', 'D')

在这里我们初始化了一个有5个节点、6条边的有向图，注意，在给有向图添加边的时候，节点的顺序非常重要，第一个节点代表起点，第二个节点代表终点。

2. 网络基本性质

在network中可以直接计算网络的基本性质。

num_nodes = nx.number_of_nodes(G) #节点书
num_edges = nx.number_of_edges(G) #连接数
density = nx.density(G) #密度
clusterint_coefficient = nx.average_clustering(G) #平均聚集系数/局部聚集系数   
transitivity = nx.transitivity(G) #传递性/全局聚集系数
reciprocity = nx.reciprocity(G) #互惠性

print('节点个数: ', num_nodes)
print('连接数: ', num_edges)
print('密度: ', density)
print('局部聚集系数: ', clusterint_coefficient)
print('全局聚集系数: ', transitivity)
print('互惠性: ', reciprocity)

输出为：

节点个数:  5
连接数:  6
密度:  0.3
局部聚集系数:  0.15333333333333332
全局聚集系数:  0.25
互惠性:  0.3333333333333333

3. 中心度计算

在networkx中计算出来的中心度均为相对中心度。

out_degree = nx.out_degree_centrality(G) #出度中心度
in_degree = nx.in_degree_centrality(G) #入度中心度
out_closeness = nx.closeness_centrality(G.reverse()) #出接近中心度
in_closeness = nx.closeness_centrality(G) #入接近中心度
betweenness = nx.betweenness_centrality(G) #中介中心度

print('出度中心度: ', out_degree)
print('入度中心度: ', in_degree)
print('出接近中心度: ', out_closeness)
print('入接近中心度: ', in_closeness)
print('中介中心度: ', betweenness)

输出为：

出度中心度:  {'A': 0.5, 'B': 0.5, 'D': 0.25, 'C': 0.0, 'E': 0.25}
入度中心度:  {'A': 0.0, 'B': 0.25, 'D': 0.75, 'C': 0.25, 'E': 0.25}
出接近中心度:  {'A': 0.6666666666666666, 'B': 0.5625, 'D': 0.25, 'C': 0.0, 'E': 0.25}
入接近中心度:  {'A': 0.0, 'B': 0.25, 'D': 0.75, 'C': 0.3333333333333333, 'E': 0.44999999999999996}
中介中心度:  {'A': 0.0, 'B': 0.08333333333333333, 'D': 0.16666666666666666, 'C': 0.0, 'E': 0.0}

4. 中心势计算

在networkx中没有似乎没有直接计算中心势的方法，这里我们可以根据公式自己计算。

max_ = 0
s = 0
for out in out_degree.keys():
        if(out_degree[out] > max_): max_ = out_degree[out]
        s = s + out_degree[out]
print('出度中心势：', (num_nodes * max_ - s) / (num_nodes - 2))

max_ = 0
s = 0
for in_ in in_degree.keys():
    if(in_degree[in_] > max_): max_ = in_degree[in_]
    s = s + in_degree[in_]
print('入度中心势：', (num_nodes * max_ - s) / (num_nodes - 2))

max_ = 0
s = 0
for b in out_closeness.keys():
    if(out_closeness[b] > max_): max_ = out_closeness[b]
    s = s + out_closeness[b]
print('出接近中心势：', (num_nodes * max_ - s) / (num_nodes- 1) / (num_nodes - 2) * (2 * num_nodes - 3))

max_ = 0
s = 0
for b in in_closeness.keys():
    if(in_closeness[b] > max_): max_ = in_closeness[b]
    s = s + in_closeness[b]
print('入接近中心势：', (num_nodes * max_ - s) / (num_nodes- 1) / (num_nodes - 2) * (2 * num_nodes - 3))

max_ = 0
s = 0
for b in betweenness.keys():
    if(betweenness[b] > max_): max_ = betweenness[b]
    s = s + betweenness[b]
print('中介中心势：', (num_nodes * max_ - s) / (num_nodes - 1))

输出为：

出度中心势： 0.3333333333333333
入度中心势： 0.75
出接近中心势： 0.9357638888888888
入接近中心势： 1.1472222222222221
中介中心势： 0.14583333333333331

5. 绘制

import matplotlib.pyplot as plt
nx.draw(G)
plt.show()

人与人之间的相互联系构成了我们这里将要讨论的社会网络。网络由节点（node）和连接它们的边（edge）构成。例如，你的微信好友可以看作是网络中的一个节点，而连接节点的边可以看作是朋友关系。在万维网中，每个网页是一个节点，而从一个页面到另一个页面的超链接则是这个网络的边。

微信好友的关系是相互的，如果我是你的好友，你也是我的好友。这样的网络称为无向网络(undirected graph/network)。但超链接并非如此，如果我的网站可以链接到维基百科，并不表示维基百科会链接到我的网站。这样的网络称为有向网络(directed graph/network)。

在图论和网络分析中，中心性（Centrality）是判断网络中节点重要性/影响力的指标。在社会网络分析中，一项基本的任务就是鉴定一群人中哪些人比其他人更有影响力，从而帮助我们理解他们在网络中扮演的角色。

那么，什么样的节点是重要的呢？

对节点重要性的解释有很多，不同的解释下判定中心性的指标也有所不同。

 

 

2. 中介中心性（betweenness centrality）

网络中两个非相邻成员之间的相互作用依赖于其他成员，特别是两成员之间路径上的那些成员。他们对两个非相邻成员之间的相互作用具有控制和制约作用。Freeman (1979)认为中间成员对路径两端的成员具有“更大的人际关系影响”。因此，中介中心性的思想是：如果一个成员位于其他成员的多条最短路径上，那么该成员就是核心成员，就具有较大的中介中心性。

计算网络中任意两个节点的所有最短路径，如果这些最短路径中很多条都经过了某个节点，那么就认为这个节点的中介中心性高。回到上面的蝴蝶结网络，假设我们要计算节点D的中介中心性。

 

  • 首先，我们计算节点D之外，所有节点对之间的最短路径有多少条，这里是15条（在6个节点中选择两个节点即节点对的个数）。
  • 然后，我们再看所有这些最短路径中有多少条经过节点D，例如节点A要想找到节点E，必须经过节点D。经过节点D的最短路径有9条。
  • 最后，我们用经过节点D的最短路径除以所有节点对的最短路径总数，这个比率就是节点D的中介中心性。节点D的中介中心性是9/15=0.6。

 

如果说点度中心性发现的是网络中的“名人”，那么中介中心性的现实意义是什么呢？

Maksim Tsvetovat&Alexander Kouznetsov在《社会网络分析》一书中有两个例子：

 

  • 鲍勃徘徊在两个女人之间，他贪恋爱丽丝的美丽和谈吐，亦无法舍弃卡若琳娜的乐天和无忧无虑。但他必须小心谨慎，生怕自己在其中任何一个人面前露馅，这样的关系充满了压力和焦虑
  • 银行家以5%的利率接受A公司的存款，以7%的利率贷款给B公司，这样的关系给银行家带来了巨大的利益。它的前提是，市场中的A公司和B公司不能直接接触，或至少无法轻易地找到对方

 

鲍勃和银行家的故事尽管截然不同，但他们都处于一种被称为被禁止的三元组(forbidden triad)的关系中，需要确保三元组的末端不能直接联系。没有联系就像网络中出现了一个洞，因此也被称为结构洞。

当网络中众多成员的接触或低成本接触都依赖我时，我就对其他成员有了控制和制约作用。我可以利用这种关系控制信息的流动，套取巨大的利益。当然，这样的关系也充满着压力和紧张。诚如Maksim Tsvetovat&Alexander Kouznetsov所言，商人的成功，不仅取决于他们对不对称信息的利用和经营能力，也需要对创造和维持套利机会带来的压力的高度容忍。

 

3. 接近中心性（closeness centrality）

点度中心性仅仅利用了网络的局部特征，即节点的连接数有多少，但一个人连接数多，并不代表他/她处于网络的核心位置。接近中心性和中介中心性一样，都利用了整个网络的特征，即一个节点在整个结构中所处的位置。如果节点到图中其他节点的最短距离都很小，那么它的接近中心性就很高。相比中介中心性，接近中心性更接近几何上的中心位置。

假设我们要计算节点D的接近中心性，首先我们计算从节点D到所有其他节点的最短距离。从图中可以判断，节点D到所有其他节点的距离均为1，距离之和为6。因此，节点D的接近中心性为(7-1)/6=1。分子为网络中节点总数减去1。也就是说，如果一个人可以直接跟网络中所有其他人联系，那么他/她的接近中心性就是1。对于其他节点，如节点A的接近中心性为(7-1)/9=0.667。

接近中心性高的节点一般扮演的是八婆的角色（gossiper）。他们不一定是名人，但是乐于在不同的人群之间传递消息。

 

4. 特征向量中心性（eigenvector centrality）

特征向量中心性的基本思想是，一个节点的中心性是相邻节点中心性的函数。也就是说，与你连接的人越重要，你也就越重要。

特征向量中心性和点度中心性不同，一个点度中心性高即拥有很多连接的节点特征向量中心性不一定高，因为所有的连接者有可能特征向量中心性很低。同理，特征向量中心性高并不意味着它的点度中心性高，它拥有很少但很重要的连接者也可以拥有高特征向量中心性。

考虑下面的图，以及相应的5x5的邻接矩阵(Adjacency Matrix)，A。

 

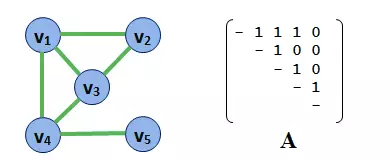
邻接矩阵的含义是，如果两个节点没有直接连接，记为0，否则记为1。

现在考虑x，一个5x1的向量，向量的值对应图中的每个点。在这种情况下，我们计算的是每个点的点度中心性（degree centrality），即以点的连接数来衡量中心性的高低。

矩阵A乘以这个向量的结果是一个5x1的向量：

 

 

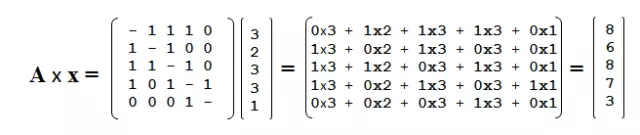
结果向量的第一个元素是用矩阵A的第一行去“获取”每一个与第一个点有连接的点的值（连接数，点度中心性），也就是第2个、第3个和第4个点的值，然后将它们加起来。

换句话说，邻接矩阵做的事情是将相邻节点的求和值重新分配给每个点。这样做的结果就是“扩散了”点度中心性。你的朋友的朋友越多，你的特征向量中心性就越高。

 

 

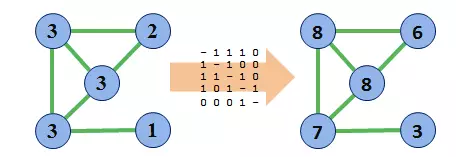
我们继续用矩阵A乘以结果向量。如何理解呢？实际上，我们允许这一中心性数值再次沿着图的边界“扩散”。我们会观察到两个方向上的扩散（点既给予也收获相邻节点）。我们猜测，这一过程最后会达到一个平衡，特定点收获的数量会和它给予相邻节点的数量取得平衡。既然我们仅仅是累加，数值会越来越大，但我们最终会到达一个点，各个节点在整体中的比例会保持稳定。

现在把所有点的数值构成的向量用更一般的形式表示：

 

 

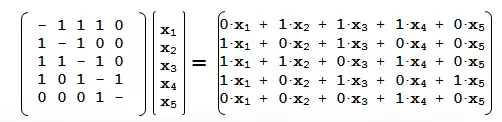
我们认为，图中的点存在一个数值集合，对于它，用矩阵A去乘不会改变向量各个数值的相对大小。也就是说，它的数值会变大，但乘以的是同一个因子。用数学符号表示就是：

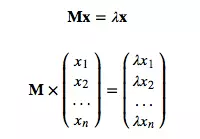
满足这一属性的向量就是矩阵M的特征向量。特征向量的元素就是图中每个点的特征向量中心性。

特征向量中心性的计算需要读者具备矩阵乘法和特征向量的知识，但不影响这里读者对特征向量中心性思想的理解，不再赘述。

 

5. 有向图与PageRank

PageRank是衡量有向网络中节点重要性的指标。

我们将万维网抽象成有向图：（1）每个网页抽象成一个节点，假设有A、B、C、D四个节点；（2）用户通过超链接在网页之间跳转，这种跳转是有方向的（directed），从网页A跳转到网页B不代表可以从网页B链接到网页A，这种节点之间的有方向的连接被抽象成有方向的边。整个网络构成一个有向图。

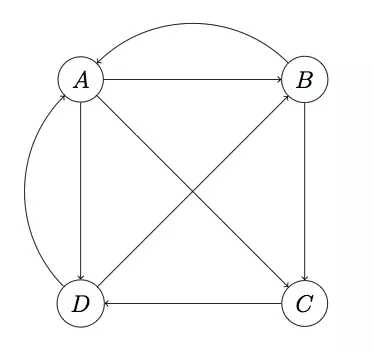
你可以很轻易地找到最受欢迎的网页。但是，PageRank的思想认为，指标最好还需要考虑到指向你的那些网页。也就是说，来自受欢迎的网页的跳转应该重于不太受欢迎的网页的跳转。这就是PageRank思想的精华，Google就是利用这一思想来给网站排名的。这里的思想依据和特征向量中心性其实是一致的。

首先，我们假设用户停留在一个页面时，跳转到每个链接页面的概率是相同的。例如，用户停留在页面A，他可以跳转到B、C、D三个页面，我们假设用户跳转到每个页面的概率相同，也就是说用户跳转到每个页面的概率均为1/3。我们可以用下面的转移矩阵（Transition Matrix）来表示整个有向图的情况：

 

 

假设有向图中有n个节点，那么M就是一个n行n列的矩阵，其中的第i行第j列代表从页面j跳转到页面i的概率。例如，M矩阵的第一行代表从ABCD跳转到页面A的概率。

然后，我们设每个页面的初始rank为1/4，4个页面的初始rank构成向量v：

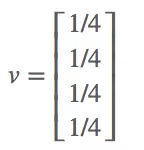
用M第一行乘以向量v，得到的就是页面A最新rank的合理估计：0*1/4+1/2*1/4+0*1/4+1/2*1/4=1/4。Mv的结果就是ABCD四个页面的新rank：

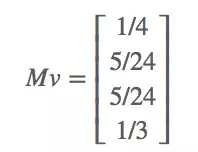
然后用M再乘以新的rank向量，又会产生一个新的rank向量。迭代这一过程，Mv结果各个值的相对大小会保持稳定。也就是说，其结果等于用一个标量乘以v。

满足这一属性的向量就是矩阵M的特征向量。这里的结果会收敛在[1/4, 1/4, 1/5, 1/4]，这就是A、B、C、D最后的PageRank。这一结果表明，相比于网页C, ABD更为重要。

上述方程式假设上网者一定是通过网页上的链接进行跳转的，但实际上，上网者在每一步都有可能在地址栏随机输入一个网址，跳转到其他页面，而不是点击网页上的链接。或者，上网者可能到达一个没有任何链出页面的网页，这时他会随机到另外的页面进行浏览。

想象有两个网页的简单例子，网页A链接到B，但B无法链接到A。转移矩阵如下：

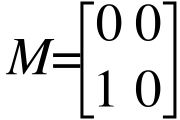
不断迭代，最后我们得到的是一个0矩阵：

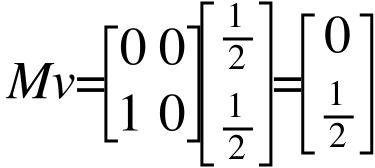
考虑到B比A重要，这一结果是不合理的，它认为A和B同等重要。为了解决这个问题，我们引入“心灵运输”（Teleportation）的概念。它意味着上网者每一步都有可能随机输入一个网址（心灵运输），跳转到其他页面（这意味着每一步，网络上的每个网页都有一定的概率被访问到，它的概率为(1-d)/N，即上网者心灵运输的概率乘以每个网页被访问的概率），而不是点击网页上的链接。

我们假设上网者在任何页面继续向下浏览的概率为d=0.85。d也被称为阻尼系数（damping factor）。1-d=0.15就是上网者停止点击，随机跳到新网址的概率，即心灵运输的概率。设网页总数为N，那么跳转到任一网页的概率为N。因此，调整后的方程式如下：

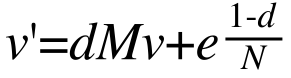
其中的e为单位矩阵，这样才能与方程式的前半部分相加。

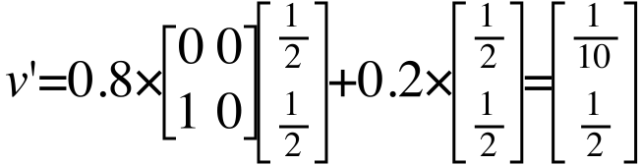
不断迭代后，两个网页的rank会收敛为：

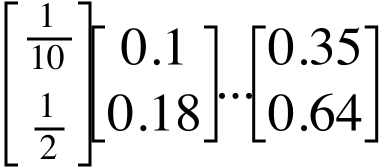
6. 小结

  1. 点度中心性：一个人的社会关系越多，他/她就越重要
  2. 中介中心性：如果一个成员处于其他成员的多条最短路径上，那么该成员就是核心成员
  3. 接近中心性：一个人跟所有其他成员的距离越近，他/她就越重要
  4. 特征向量中心性：与你连接的人社会关系越多，你就越重要
  5. PageRank：来自受欢迎的网页的跳转应该重于不太受欢迎的网页的跳转

 

任何一个实际网络不可能只符合某一种类型的复杂网络。至今为止提出的所有类型的复杂网络，包括小世界、无标度、同配性/异配性、社团化、阵发性等等类型的复杂网络，都是从一个角度分析实际网络。所以是先采样实际网络的数据，然后对数据利用网络指标，包括聚类系数，平均路径长度，度分布，度度相关性等等，对比将真实网络进行不同的随机化处理后的对照网络，识别其是否符合某一类复杂网络的标准特征。

如果你自己真的构造一个网络，而不是复现他人已经提出来的网络模型，那么你一定非常清楚你构造网络算法对应的机制是什么？然后你要首先猜测你的机制和哪个真实网络的产生演化机制相类似，然后找到你构造网络与已有类型的复杂网络的区别，并分析这个区别是否和某个你认为具有相同生成机制的真实网络匹配。

从研究方法上，不建议题主这样研究，而是应该从真实网络数据出发，先找到和已有类型复杂网络不同的特征，然后分析可能的产生机制，最后利用该机制生成算法构造成网络。



.1平均路径长度L

在网络中，两点之间的距离为连接两点的最短路径上所包含的边的数目。网络的平均路径长度指网络中所有节点对的平均距离，它表明网络中节点间的分离程度，反映了网络的全局特性。不同的网络结构可赋予L不同的含义。如在疾病传播模型中L可定义为疾病传播时间，通网络模型中L可定义为站点之间的距离等。

2.2聚集系数C

在网络中，节点的聚集系数是指与该节点相邻的所有节点之间连边的数目占这些相邻节点之间最大可能连边数目的比例。而网络的聚集系数则是指网络中所有节点聚集系数的平均值，它表明网络中节点的聚集情况即网络的聚集性，也就是说同一个节点的两个相邻节点仍然是相邻节点的概率有多大，它反映了网络的局部特性。

2.3度及度分布

在网络中，点的度是指与该节点相邻的节点的数目，即连接该节点的边的数目。而网络的度<k>指网络中所有节点度的平均值。度分布P(k)指网络中一个任意选择的节点，它的度恰好为k的概率。

2.4介数

包括节点介数和边介数。节点介数指网络中所有最短路径中经过该节点的数量比例，边介数则指网络中所有最短路径中经过该边的数量比例。介数反映了相应的节点或边在整个网络中的作用和影响力。

2.5小世界效应

复杂网络的小世界效应是指尽管网络的规模很大(网络节点数目N很大)，但是两个节点之间的距离比我们想象的要小得多。也就是网络的平均路径长度L随网络的规模呈对数增长，即L～In N。大量的实证研究表明，真实网络几乎都具有小世界效应。

2.6无标度特性

对于随机网络和规则网络，度分布区间非常狭窄，大多数节点都集中在节点度均值<k>的附近，说明节点具有同质性，因此<k>可以被看作是节点度的一个特征标度。而在节点度服从幂律分布的网络中，大多数节点的度都很小，而少数节点的度很大，说明节点具有异质性，这时特征标度消失。这种节点度的幂律分布为网络的无标度特性。

参考资料：

1. Great Power Law, 节点的中心度（Centrality）

2. WIKIPEDIA, Betweenness Centrality, Eigenvector Centrality, PageRank

3.Dan Ryan, eigenvector centrality()

4. 张洋, 浅析PageRank算法

5. Tavish Srivastava, PageRank explained in simple terms!

6. Joel Grus, 数据科学入门

7. networkx官方文档, 

8. Maksim Tsvetovat&Alexander Kouznetsov, 社会网络分析, 机械工业出版社

9. 部分图片来自网络




posted @ 2020-07-04 18:45  白云君  阅读(13227)  评论(1)  编辑  收藏  举报