李航-统计学习方法-第一章习题答案

第一章

1.1 说明伯努利模型的极大似然估计以及贝叶斯估计中的统计学习方法三要素。

答：

统计学习方法的三要素是模型、策略、算法。

 

	模型	策略	算法
极大似然估计	条件概率	经验风险最小化	求解析解
贝叶斯估计	条件概率	结构风险最小化	求数值解

伯努利模型是定义在取值为0和1的随机变量上的概率分布。

 

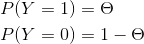
极大似然估计：

 

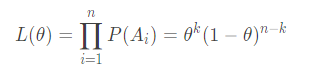
似然函数的对数：

 

 

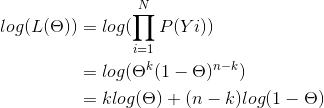
其中，n为实验次数，k为n次实验中结果为1的次数，Yi表示第i次实验的结果。

令对数似然的导数为0可以直接求出解析解：

 

 

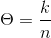
贝叶斯估计：

 

 

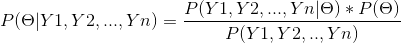
根据先验概率和估计后验概率，使后验概率最大化。

所以贝叶斯估计得到的概率取决于所选择的先验分布。

PS:对于伯努利模型，可以使用beta分布作为贝叶斯估计的先验概率。

1.2  证明：模型是条件概率分布，当损失函数是对数损失时，经验风险最小化等价于极大似然估计。

首先需要理解几个概念，条件概率分布，对数损失，经验风险和极大似然估计。

模型是条件概率分布，说明预测值：

对数损失的定义为：

此时，经验风险R为：

 

所以，最小化经验风险R，相当于最大化似然估计