数据结构——基于java的链表实现（真正理解链表这种数据结构）

原创不易，如需转载，请注明出处https://www.cnblogs.com/baixianlong/p/10759599.html，否则将追究法律责任！！！

一、链表介绍

1、什么是链表？

• 链表是一种物理存储结构上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。如下图所示，在数据结构中，a1里面的指针存储着a2的地址，这样一个链接一个，就形成了链表。
  
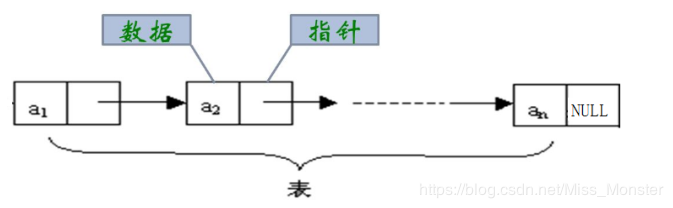
  • 相邻元素之间通过指针链接
  • 最后一个元素的后继指针为NULL
  • 在程序执行过程中，链表的长度可以增加或缩小
  • 链表的空间能够按需分配
  • 没有内存空间的浪费

2、链表的优缺点？

• 优点：

  • 插入和删除时不需移动其他元素, 只需改变指针,效率高。
  • 链表各个节点在内存中空间不要求连续，空间利用率高。
  • 大小没有固定，拓展很灵活。

• 缺点：

  • 查找数据时效率低，因为不具有随机访问性。

3、链表的种类？

• 有单链表、双向链表、循环单链表、循环双链表等等。

二、单链的实现和相关操作

1、链表类的创建（以下均已单链表为基准）

public class SingleLinkedList {
	//head为头节点，他不存放任何的数据，只是充当一个指向链表中真正存放数据的第一个节点的作用
	public Node head = new Node();  

    //内部类,定义node节点,使用内部类的最大好处是可以和外部类进行私有操作的互相访问
    class Node{
        public int val;  //int类型会导致head节点的val为0，不影响我们学习
        public Node next;
        public Node(){}
        public Node(int val){
            this.val = val;
        }
    } 

	//下面就可以自定义各种链表操作。。。
}

2、链表添加结点

//找到链表的末尾结点，把新添加的数据作为末尾结点的后续结点
public void add(int data){
    if (head.next == null){
        head.next = new Node(data);
        return;
    }
    Node temp = head;
    while (temp.next != null){
        temp = temp.next;
    }
    temp.next = new Node(data);
}

3、链表删除节点

//把要删除结点的前结点指向要删除结点的后结点，即直接跳过待删除结点
public boolean deleteNode(int index){
    if (index < 0 || index > length() ){
        return false;
    }
    if (index == 1){ //删除头结点
        head = head.next;
        return true;
    }
    Node preNode = head;
    Node curNode = preNode.next;
    int i = 2;
    while (curNode!=null){
        if (index == i){
            preNode.next = curNode.next;  //指向删除节点的后一个节点
            break;
        }
        preNode = curNode;
        curNode = preNode.next;
        i++;
    }
    return true;
}

4、链表长度、节点获取以及链表遍历

//获取链表长度
public int length(){
    int length = 0;
    Node temp = head;
    while (temp.next!=null){
        length++;
        temp = temp.next;
    }
    return length;
}


//获取最后一个节点
public Node getLastNode(){
    Node temp = head;
    while (temp.next != null){
        temp = temp.next;
    }
    return temp;
}


//获取第index节点
public Node getNodeByIndex(int index){
    if(index<1 || index>length()){
        return null;
    }
    Node temp = head;
    int i = 1;
    while (temp.next != null){
        temp = temp.next;
        if (index==i){
            break;
        }
        i++;
    }
    return temp;
}


//打印节点
public void printLink(){
    Node curNode = head;
    while(curNode !=null){
        System.out.print(curNode.val+" ");
        curNode = curNode.next;
    }
}

5、查找单链表中的倒数第n个结点

//两个指针，第一个指针向前移动k-1次，之后两个指针共同前进，当前面的指针到达末尾时，后面的指针所在的位置就是倒数第k个位置
public Node findReverNode(int index){
    if(index<1 || index>length()){
        return null;
    }
    Node first = head;
    Node second = head;
    for (int i = 0; i < index - 1; i++) {
        second = second.next;
    }
    while (second.next != null){
        first = first.next;
        second = second.next;
    }
    return first;
}

6、查找单链表中的中间结点

//也是设置两个指针first和second，只不过这里是，两个指针同时向前走，second指针每次走两步，
//first指针每次走一步，直到second指针走到最后一个结点时，此时first指针所指的结点就是中间结点。
public Node findMiddleNode(){
    Node slowPoint = head;
    Node quickPoint = head;
    //链表结点个数为奇数时,返回的是中间结点；链表结点个数为偶数时，返回的是中间两个结点中的前个
    while(quickPoint != null && quickPoint.next != null){
        slowPoint = slowPoint.next;
        quickPoint = quickPoint.next.next;
    }
    return slowPoint;
}

7、从尾到头打印单链表

//方法一：先反转链表，再输出链表，需要链表遍历两次(不建议这么做,改变了链表的结构)
。。。
//方法二、通过递归来实现（链表很长的时候，就会导致方法调用的层级很深，有可能造成StackOverflowError）
public void reservePrt(Node node){
    if(node != null){
        reservePrt(node.next);
        System.out.print(node.val+" ");
    }
}

//方法三、把链表中的元素放入栈中再输出，需要维护额外的栈空间
public void reservePrt2(Node node){
    if(node != null){
        Stack<Node> stack = new Stack<Node>();  //新建一个栈
        Node current = head;
        //将链表的所有结点压栈
        while (current != null) {
            stack.push(current);  //将当前结点压栈
            current = current.next;
        }
        //将栈中的结点打印输出即可
        while (stack.size() > 0) {
            System.out.print(stack.pop().val+" ");  //出栈操作
        }
    }
}

8、单链表的反转(1->2->3->4变为4->3->2->1)

//从头到尾遍历原链表，每遍历一个结点，将其摘下放在新链表的最前端。注意链表为空和只有一个结点的情况。时间复杂度为O（n）
public void reserveLink(){
    Node curNode = head;
    Node preNode = null;
    while (curNode.next != null){
        Node nextNode = curNode.next;
		//主要理解以下逻辑
        curNode.next = preNode; //将current的下一个结点指向新链表的头结点
        preNode = curNode;  //将改变了指向的cruNode赋值给preNode
        curNode = nextNode;
    }
    curNode.next = preNode;
    preNode = curNode;
    head = preNode;
}

9、判断链表是否有环

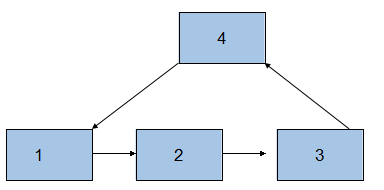
//设置快指针和慢指针，慢指针每次走一步，快指针每次走两步,当快指针与慢指针相等时，就说明该链表有环
public boolean isRinged(){
    if(head == null){
        return false;
    }
    Node slow = head;
    Node fast = head;
    while(fast.next != null && fast.next.next != null){
        slow = slow.next;
        fast = fast.next.next;
        if(fast == slow){
            return true;
        }
    }
    return false;
}

10、取出有环链表中，环的长度

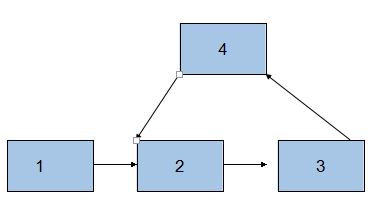
//获取环的相遇点
public Node getFirstMeet(){
    if(head == null){
        return null;
    }
    Node slow = head;
    Node fast = head;
    while(fast.next != null && fast.next.next != null){
        slow = slow.next;
        fast = fast.next.next;
        if(fast == slow){
            return slow;
        }
    }
    return null;
}

//首先得到相遇的结点，这个结点肯定是在环里，我们可以让这个结点对应的指针一直往下走，直到它回到原点，就可以算出环的长度
public int getCycleLength(){
    Node current = getFirstMeet(); //获取相遇点
    int length = 0;
    while (current != null) {
        current = current.next;
        length++;
        if (current == getFirstMeet()) {  //当current结点走到原点的时候
            return length;
        }
    }
    return length;
}

11、判断两个链表是否相交

//两个链表相交，则它们的尾结点一定相同，比较两个链表的尾结点是否相同即可
public boolean isCross(Node head1, Node head2){
    Node temp1 = head1;
    Node temp2 = head2;
    while(temp1.next != null){
        temp1 = temp1.next;
    }
    while(temp2.next != null){
        temp2 = temp2.next;
    }
    if(temp1 == temp2){
        return true;
    }
    return false;
}

12、如果链表相交，求链表相交的起始点

 /**
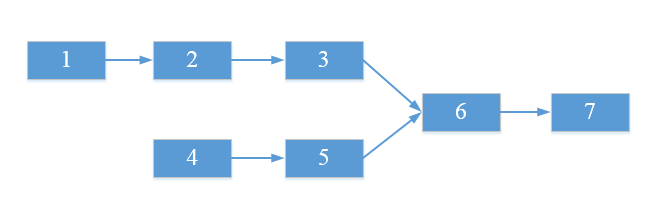
 * 如果链表相交，求链表相交的起始点：
 * 1、首先判断链表是否相交，如果两个链表不相交，则求相交起点没有意义
 * 2、求出两个链表长度之差：len=length1-length2
 * 3、让较长的链表先走len步
 * 4、然后两个链表同步向前移动，每移动一次就比较它们的结点是否相等，第一个相等的结点即为它们的第一个相交点
 */
public Node findFirstCrossPoint(SingleLinkedList linkedList1, SingleLinkedList linkedList2){
    //链表不相交
    if(!isCross(linkedList1.head,linkedList2.head)){
        return null;
    }else{
        int length1 = linkedList1.length();//链表1的长度
        int length2 = linkedList2.length();//链表2的长度
        Node temp1 = linkedList1.head;//链表1的头结点
        Node temp2 = linkedList2.head;//链表2的头结点
        int len = length1 - length2;//链表1和链表2的长度差

        if(len > 0){//链表1比链表2长，链表1先前移len步        
            for(int i=0; i<len; i++){
                temp1 = temp1.next;
            }
        }else{//链表2比链表1长，链表2先前移len步
            for(int i=0; i<len; i++){
                temp2 = temp2.next;
            }
        }
        //链表1和链表2同时前移,直到找到链表1和链表2相交的结点
        while(temp1 != temp2){
            temp1 = temp1.next;
            temp2 = temp2.next;
        }
        return temp1;
    }
}

13、合并两个有序的单链表（将1->2->3和1->3->4合并为1->1->2->3->3->4）

//两个参数代表的是两个链表的头结点
//方法一
public Node mergeLinkList(Node head1, Node head2) {
    if (head1 == null && head2 == null) {  //如果两个链表都为空
        return null;
    }
    if (head1 == null) {
        return head2;
    }
    if (head2 == null) {
        return head1;
    }
    Node head; //新链表的头结点
    Node current;  //current结点指向新链表
    // 一开始，我们让current结点指向head1和head2中较小的数据，得到head结点
    if (head1.val <= head2.val) {
        head = head1;
        current = head1;
        head1 = head1.next;
    } else {
        head = head2;
        current = head2;
        head2 = head2.next;
    }

    while (head1 != null && head2 != null) {
        if (head1.val <= head2.val) {
            current.next = head1;  //新链表中，current指针的下一个结点对应较小的那个数据
            current = current.next; //current指针下移
            head1 = head1.next;
        } else {
            current.next = head2;
            current = current.next;
            head2 = head2.next;
        }
    }
    //合并剩余的元素
    if (head1 != null) { //说明链表2遍历完了，是空的
        current.next = head1;
    }
    if (head2 != null) { //说明链表1遍历完了，是空的
        current.next = head2;
    }
    return head;
}


//方法二：递归法
public Node merge(Node head1, Node head2) {
        if(head1 == null){
            return head2;
        }
        if(head2 == null){
            return head1;
        }
        Node head = null;
        if(head1.val <= head2.val){
            head = head1;
            head.next = merge(head1.next,head2);
        }else{
            head = head2;
            head.next = merge(head1,head2.next);
        }
        return head;
    }

到此单链表的一些常见操作展示的差不多了,如有兴趣可继续深入研究~~~

三、其它种类链表（拓展）

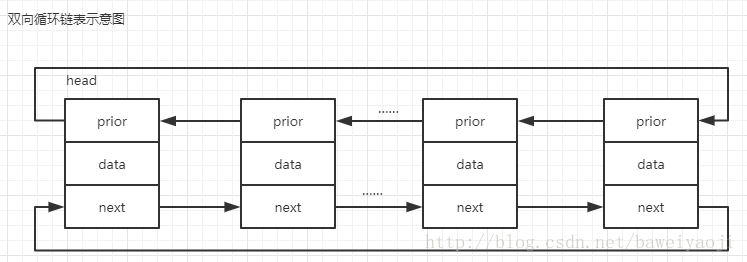
1、双向链表（java.util中的LinkedList就是双链的一种实现）

　　双向链表(双链表)是链表的一种。和单链表一样，双链表也是由节点组成，它的每个数据结点中都有两个指针，分别指向直接后继和直接前驱。所以，从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点。一般我们都构造双向循环链表。

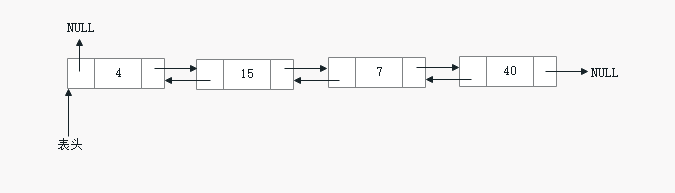
• 优点：对于链表中一个给的的结点，可以从两个方向进行操，双向链表相对单链表更适合元素的查询工作。
• 缺点：
  • 每个结点需要再添加一个额外的指针，因此需要更多的空间开销。
  • 结点的插入或者删除更加费时。

以下是双链的相关实现和操作(其实单链弄明白了，双链只不过多维护了个前节点)

public class DoubleLink<T> {

    // 表头
    private DNode<T> mHead;
    // 节点个数
    private int mCount;

    // 双向链表“节点”对应的结构体
    private class DNode<T> {
        public DNode prev;
        public DNode next;
        public T value;

        public DNode(T value, DNode prev, DNode next) {
            this.value = value;
            this.prev = prev;
            this.next = next;
        }
    }

    // 构造函数
    public DoubleLink() {
        // 创建“表头”。注意：表头没有存储数据！
        mHead = new DNode<T>(null, null, null);
        mHead.prev = mHead.next = mHead;
        // 初始化“节点个数”为0
        mCount = 0;
    }

    // 返回节点数目
    public int size() {
        return mCount;
    }

    // 返回链表是否为空
    public boolean isEmpty() {
        return mCount==0;
    }

    // 获取第index位置的节点
    private DNode<T> getNode(int index) {
        if (index<0 || index>=mCount)
            throw new IndexOutOfBoundsException();

        // 正向查找
        if (index <= mCount/2) {
            DNode<T> node = mHead.next;
            for (int i=0; i<index; i++)
                node = node.next;

            return node;
        }

        // 反向查找
        DNode<T> rnode = mHead.prev;
        int rindex = mCount - index -1;
        for (int j=0; j<rindex; j++)
            rnode = rnode.prev;

        return rnode;
    }

    // 获取第index位置的节点的值
    public T get(int index) {
        return getNode(index).value;
    }

    // 获取第1个节点的值
    public T getFirst() {
        return getNode(0).value;
    }

    // 获取最后一个节点的值
    public T getLast() {
        return getNode(mCount-1).value;
    }

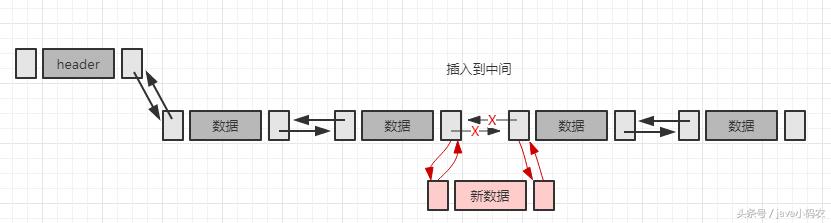
    // 将节点插入到第index位置之前
    public void insert(int index, T t) {
        if (index==0) {
            DNode<T> node = new DNode<T>(t, mHead, mHead.next);
            mHead.next.prev = node;
            mHead.next = node;
            mCount++;
            return ;
        }

        DNode<T> inode = getNode(index);
        DNode<T> tnode = new DNode<T>(t, inode.prev, inode);
        inode.prev.next = tnode;
        inode.next = tnode;
        mCount++;
        return ;
    }

    // 将节点插入第一个节点处。
    public void insertFirst(T t) {
        insert(0, t);
    }

    // 将节点追加到链表的末尾
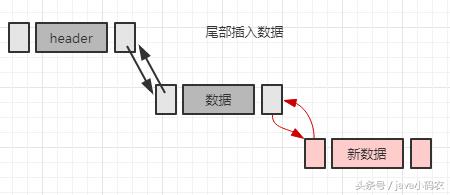
    public void appendLast(T t) {
        DNode<T> node = new DNode<T>(t, mHead.prev, mHead);
        mHead.prev.next = node;
        mHead.prev = node;
        mCount++;
    }

    // 删除index位置的节点
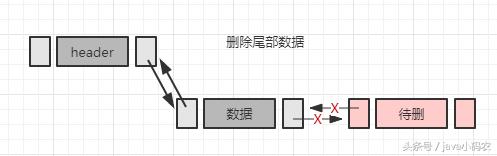
    public void del(int index) {
        DNode<T> inode = getNode(index);
        inode.prev.next = inode.next;
        inode.next.prev = inode.prev;
        inode = null;
        mCount--;
    }

    // 删除第一个节点
    public void deleteFirst() {
        del(0);
    }

    // 删除最后一个节点
    public void deleteLast() {
        del(mCount-1);
    }
}

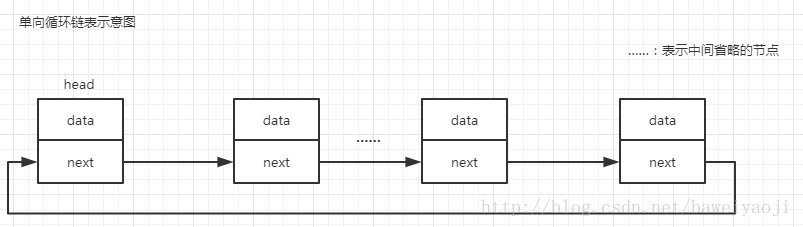
2、循环单链表、循环双链表（操作和单链、双链是一样的，不赘述了）

四、总结

• 本文主要是对于链表这种数据结构的介绍和认知，明白链表的优劣势。
• 重点是要学会对于单链的操作，体会它的一些独到之处，至于其它衍生链表，举一反三而已！！！

个人博客地址：

cnblogs:https://www.cnblogs.com/baixianlong
csdn:https://blog.csdn.net/tiantuo6513
segmentfault:https://segmentfault.com/u/baixianlong
github:https://github.com/xianlongbai