jaccard similarity coefficient 相似度计算
Jaccard index
The Jaccard index, also known as the Jaccard similarity coefficient (originally coined coefficient de communauté by Paul Jaccard), is a statisticused for comparing the similarity and diversity of sample sets. The Jaccard coefficient measures similarity between finite sample sets, and is defined as the size of the intersection divided by the size of the union of the sample sets:
(If A and B are both empty, we define J(A,B) = 1.)
The MinHash min-wise independent permutations locality sensitive hashing scheme may be used to efficiently compute an accurate estimate of the Jaccard similarity coefficient of pairs of sets, where each set is represented by a constant-sized signature derived from the minimum values of ahash function.
The Jaccard distance, which measures dissimilarity between sample sets, is complementary to the Jaccard coefficient and is obtained by subtracting the Jaccard coefficient from 1, or, equivalently, by dividing the difference of the sizes of the union and the intersection of two sets by the size of the union:
An alternate interpretation of the Jaccard distance is as the ratio of the size of the symmetric difference  to the union.
to the union.
This distance is a metric on the collection of all finite sets.[1][2]
There is also a version of the Jaccard distance for measures, including probability measures. If  is a measure on a measurable space
is a measure on a measurable space  , then we define the Jaccard coefficient by
, then we define the Jaccard coefficient by 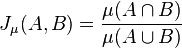 , and the Jaccard distance by
, and the Jaccard distance by  . Care must be taken if
. Care must be taken if 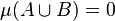 or
or 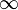 , since these formulas are not well defined in that case.
, since these formulas are not well defined in that case.


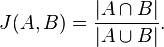
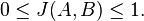


 浙公网安备 33010602011771号
浙公网安备 33010602011771号