准确率P 召回率R
Evaluation metrics
a binary classifier accuracy,specificity,sensitivety.(整个分类器的准确性，正确率，错误率)
表示分类正确：
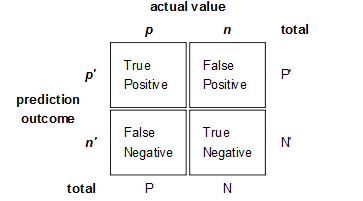
True Positive：本来是正样例，分类成正样例。
True Negative：本来是负样例，分类成负样例。
表示分类错误：
False Positive ：本来是负样例，分类成正样例，通常叫误报。
False Negative：本来是正样例，分类成负样例，通常叫漏报。
P=TP/TP+FP
R=TP/ TP+FN
F:2PR/P+R
转载一篇文章：
在信息检索、分类体系中，有一系列的指标，搞清楚这些指标对于评价检索和分类性能非常重要，因此最近根据网友的博客做了一个汇总。
准确率、召回率、F1
信息检索、分类、识别、翻译等领域两个最基本指标是召回率(Recall Rate)和准确率(Precision Rate)，召回率也叫查全率，准确率也叫查准率，概念公式:
召回率(Recall) = 系统检索到的相关文件 / 系统所有相关的文件总数
准确率(Precision) = 系统检索到的相关文件 / 系统所有检索到的文件总数
图示表示如下：
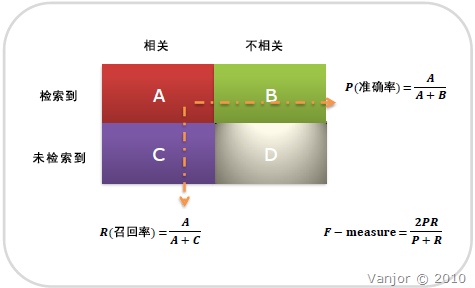
注意：准确率和召回率是互相影响的，理想情况下肯定是做到两者都高，但是一般情况下准确率高、召回率就低，召回率低、准确率高，当然如果两者都低，那是什么地方出问题了。一般情况，用不同的阀值，统计出一组不同阀值下的精确率和召回率，如下图：
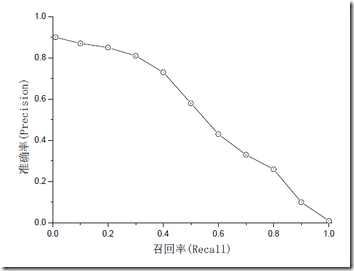
如果是做搜索，那就是保证召回的情况下提升准确率；如果做疾病监测、反垃圾，则是保准确率的条件下，提升召回。
所以，在两者都要求高的情况下，可以用F1来衡量。
- F1 = 2 * P * R / (P + R)
公式基本上就是这样，但是如何算图1中的A、B、C、D呢？这需要人工标注，人工标注数据需要较多时间且枯燥，如果仅仅是做实验可以用用现成的语料。当然，还有一个办法，找个一个比较成熟的算法作为基准，用该算法的结果作为样本来进行比照，这个方法也有点问题，如果有现成的很好的算法，就不用再研究了。
AP和mAP(mean Average Precision)
mAP是为解决P，R，F-measure的单点值局限性的。为了得到 一个能够反映全局性能的指标，可以看考察下图，其中两条曲线(方块点与圆点)分布对应了两个检索系统的准确率-召回率曲线
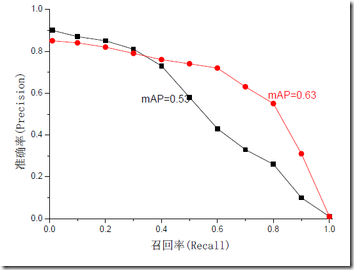
可以看出，虽然两个系统的性能曲线有所交叠但是以圆点标示的系统的性能在绝大多数情况下要远好于用方块标示的系统。
从中我们可以 发现一点，如果一个系统的性能较好，其曲线应当尽可能的向上突出。
更加具体的，曲线与坐标轴之间的面积应当越大。
最理想的系统， 其包含的面积应当是1，而所有系统的包含的面积都应当大于0。这就是用以评价信息检索系统的最常用性能指标，平均准确率mAP其规范的定义如下:(其中P，R分别为准确率与召回率)
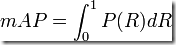
ROC和AUC
ROC和AUC是评价分类器的指标，上面第一个图的ABCD仍然使用，只是需要稍微变换。
回到ROC上来，ROC的全名叫做Receiver Operating Characteristic。
ROC关注两个指标
True Positive Rate ( TPR ) = TP / [ TP + FN] ，TPR代表能将正例分对的概率
False Positive Rate( FPR ) = FP / [ FP + TN] ，FPR代表将负例错分为正例的概率
在ROC 空间中，每个点的横坐标是FPR，纵坐标是TPR，这也就描绘了分类器在TP（真正的正例）和FP（错误的正例）间的trade-off。ROC的主要分析工具是一个画在ROC空间的曲线——ROC curve。我们知道，对于二值分类问题，实例的值往往是连续值，我们通过设定一个阈值，将实例分类到正类或者负类（比如大于阈值划分为正类）。因此我们可以变化阈值，根据不同的阈值进行分类，根据分类结果计算得到ROC空间中相应的点，连接这些点就形成ROC curve。ROC curve经过（0,0）（1,1），实际上(0, 0)和(1, 1)连线形成的ROC curve实际上代表的是一个随机分类器。一般情况下，这个曲线都应该处于(0, 0)和(1, 1)连线的上方。如图所示。
用ROC curve来表示分类器的performance很直观好用。可是，人们总是希望能有一个数值来标志分类器的好坏。
于是Area Under roc Curve(AUC)就出现了。顾名思义，AUC的值就是处于ROC curve下方的那部分面积的大小。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了较好的Performance。
AUC计算工具：
http://mark.goadrich.com/programs/AUC/
P/R和ROC是两个不同的评价指标和计算方式，一般情况下，检索用前者，分类、识别等用后者。
参考链接：
http://www.vanjor.org/blog/2010/11/recall-precision/
