数据结构与算法-1 拓扑排序 Kahn DFS 有向无环图 [MD]
| 我的GitHub | 我的博客 | 我的微信 | 我的邮箱 |
|---|---|---|---|
| baiqiantao | baiqiantao | bqt20094 | baiqiantao@sina.com |
目录
高级篇介绍
从今天开始,我们就进入了专栏的高级篇。
相对基础篇,高级篇涉及的知识点都比较零散,不是太系统。所以,我会围绕一个实际软件开发的问题,在阐述具体解决方法的过程中,将涉及的知识点给你详细讲解出来。
相较于基础篇开篇问题 - 知识讲解 - 回答开篇 - 总结 - 课后思考这样的文章结构,高级篇大致分为这样几个部分:问题阐述 - 算法解析 - 总结引申 - 课后思考。
43 | 拓扑排序
百度百科:简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
拓扑排序其实就是基于有向无环图,遍历所有的结点,每两个结点之间有先后关系。并且在搜索下一个结点的时候,这个结点之前的结点已经全部被搜索过。
拓扑排序应用非常广泛,解决的问题的模型也非常一致,凡是需要 通过局部顺序来推导全局顺序 的,一般都能用拓扑排序来解决。
如何确定代码源文件的编译顺序
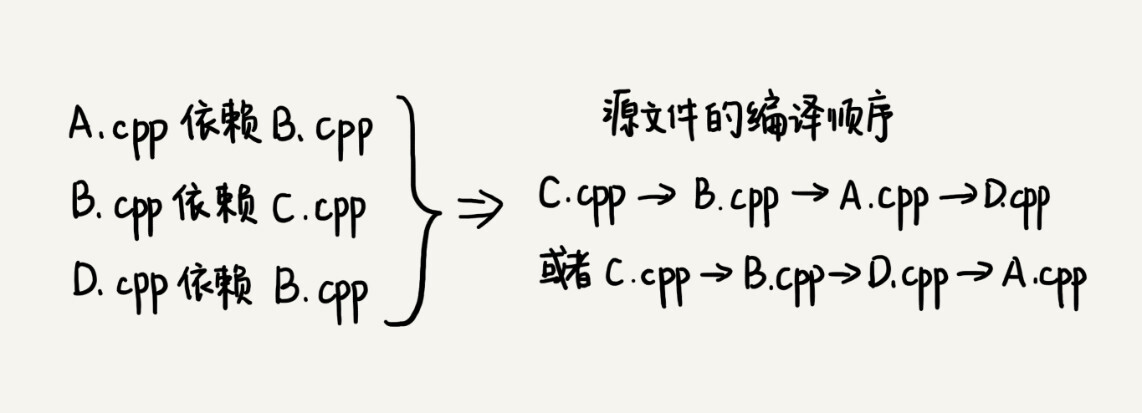
一个完整的项目往往会包含很多代码源文件,编译器在编译整个项目的时候,需要按照依赖关系,依次编译每个源文件。比如,A.cpp 依赖 B.cpp,那在编译的时候,编译器需要先编译 B.cpp,才能编译 A.cpp。
那编译器又该如何通过源文件两两之间的局部依赖关系,确定一个全局的编译顺序呢?
算法解析
有向无环图 DAG,Directed Acyclic Grap
算法是构建在具体的数据结构之上的,针对这个问题,我们可以把源文件与源文件之间的依赖关系,抽象成一个有向图。每个源文件对应图中的一个顶点,源文件之间的依赖关系就是顶点之间的边。
如果 a 先于 b 执行,也就是说 b 依赖于 a,那么就在顶点 a 和顶点 b 之间,构建一条从 a 指向 b 的边。而且,这个图不仅要是有向图,还要是一个有向无环图,也就是不能存在像 a->b->c->a 这样的循环依赖关系。因为图中一旦出现环,拓扑排序就无法工作了。实际上,拓扑排序本身就是基于有向无环图的一个算法。
public class Graph {
private int v; // 顶点的个数
private LinkedList<Integer>[] adj; // 邻接表
public Graph(int v) {
this.v = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i) {
adj[i] = new LinkedList<>(); //初始化邻接表
}
}
public void addEdge(int s, int t) {
adj[s].add(t); // s 先于 t,添加边 s->t
}
}
拓扑排序有两种实现方法,它们分别是 Kahn 算法和 DFS 深度优先搜索算法。
注意,这里的图可能不是连通的,有可能是有好几个不连通的子图构成。
Kahn 算法
Kahn 卡恩(姓氏)
Kahn 算法实际上用的是贪心算法思想,思路非常简单、好懂。
定义数据结构的时候,如果 s 需要先于 t 执行,那就添加一条 s 指向 t 的边。所以,如果某个顶点入度为 0,也就表示,没有任何顶点必须先于这个顶点执行,那么这个顶点就可以执行了。
- 先从图中找出一个入度为 0 的顶点
- 将其输出到拓扑排序的结果序列中
- 把这个顶点从图中删除,同时把这个顶点可达的顶点的入度都减 1
- 循环执行上面的过程
- 直到所有的顶点都被输出,最后输出的序列就是满足局部依赖关系的拓扑排序
这段代码实现更有技巧一些,并没有真正删除顶点的操作
// v 代表顶点的个数,adj[] 代表邻接表
public void topoSortByKahn() {
int[] inDegree = new int[v]; // 记录每个顶点的入度
for (int i = 0; i < v; ++i) { //遍历每个顶点
for (int j = 0; j < adj[i].size(); ++j) { //遍历顶点的所有边
int w = adj[i].get(j); // i->w
inDegree[w]++;
}
}
LinkedList<Integer> queue = new LinkedList<>(); //队列:先进先出
for (int i = 0; i < v; ++i) {
if (inDegree[i] == 0) queue.add(i); //存储入度为 0 的顶点(可以有多个)
}
while (!queue.isEmpty()) {
int i = queue.remove(); //移除入度为 0 的顶点
System.out.print("->" + i);
for (int j = 0; j < adj[i].size(); ++j) {
int k = adj[i].get(j);
inDegree[k]--; //移除后,此顶点指向的顶点的入度 -1
if (inDegree[k] == 0) queue.add(k); //持续存储入度为 0 的顶点
}
}
}
DFS 算法
实际上,拓扑排序也可以用深度优先搜索来实现。
public void topoSortByDFS() {
// 先构建逆邻接表(存储他依赖的顶点),边 s->t 表示,s 依赖于 t,t 先于 s
LinkedList<Integer>[] inverseAdj = new LinkedList[v];
for (int i = 0; i < v; ++i) {
inverseAdj[i] = new LinkedList<>(); //初始化
}
// 通过邻接表生成逆邻接表
for (int i = 0; i < v; ++i) {
for (int j = 0; j < adj[i].size(); ++j) {
int w = adj[i].get(j); // 存在 i->w
inverseAdj[w].add(i); // 添加 w->i
}
}
boolean[] visited = new boolean[v];
for (int i = 0; i < v; ++i) { // 深度优先遍历图
if (visited[i] == false) {
visited[i] = true;
dfs(i, inverseAdj, visited);
}
}
}
private void dfs(int vertex, LinkedList<Integer> inverseAdj[], boolean[] visited) {
for (int i = 0; i < inverseAdj[vertex].size(); ++i) {
int w = inverseAdj[vertex].get(i); //找出他依赖的顶点
if (visited[w] == true) continue; //如果依赖的顶点已经访问过,不需要重复访问
visited[w] = true;
dfs(w, inverseAdj, visited); //算法的核心:递归处理每个顶点
}
System.out.print("->" + vertex); //先输出它依赖的所有的顶点,再输出自己
}
- 邻接表中,边 s->t 表示 s 先于 t 执行,也就是 t 要依赖 s
- 在逆邻接表中,边 s->t 表示 s 依赖于 t,s 后于 t 执行
时间复杂度分析
假设 V 表示顶点个数,E 表示边的个数
- 从 Kahn 代码中可以看出来,每个顶点被访问了一次,每个边也都被访问了一次,所以,Kahn 算法的时间复杂度就是
O(V+E) - DFS 算法中,每个顶点被访问两次,每条边都被访问一次,所以时间复杂度也是
O(V+E)
因为这里的图可能不是连通的,有可能是有好几个不连通的子图构成,所以,E 并不一定大于 V,两者的大小关系不确定。所以,在表示时间复杂度的时候,V、E 都要考虑在内。
如何检测有向图中是否存在环
拓扑排序还能 检测图中环的存在。对于 Kahn 算法来说,如果最后输出出来的顶点个数,少于图中顶点个数,(也即图中还有入度不是 0 的顶点),那就说明,图中存在环。
关于图中环的检测,我们在递归那一节讲过一个例子,在查找最终推荐人的时候,可能会因为脏数据,造成存在循环推荐,如何避免这种脏数据导致的无限递归?
实际上,这就是环的检测问题。
如果我们每次都只是查找一个用户的最终推荐人,那么我们并不需要动用复杂的拓扑排序算法,而只需要记录已经访问过的用户 ID,当用户 ID 第二次被访问的时候,就说明存在环,也就说明存在脏数据。
HashSet<Integer> hashTable = new HashSet<>(); // 保存已经访问过的 actorId
public long findRootReferrerId(long actorId) {
if (hashTable.contains(actorId)) { // 存在环
return -1;
}
hashTable.add(actorId);
Long referrerId = select referrer_id from [table] where actor_id = actorId;
if (referrerId == null) return actorId;
return findRootReferrerId(referrerId); //递归遍历
}
如果我们想要知道,数据库中的所有用户之间的推荐关系中,有没有存在环的情况。这个问题,就需要用到拓扑排序算法了。我们把用户之间的推荐关系,从数据库中加载到内存中,然后构建成今天讲的这种有向图数据结构,再利用拓扑排序,就可以快速检测出是否存在环了。
2017-10-20
本文来自博客园,作者:白乾涛,转载请注明原文链接:https://www.cnblogs.com/baiqiantao/p/7700511.html


