数据结构与算法-4 朴素贝叶斯算法 欧几里得距离
目录
46 | 概率统计
如何过滤垃圾短信
实现一个简单的垃圾短信过滤功能以及骚扰电话拦截功能,该用什么样的数据结构和算法实现呢?
实际上,解决这个问题并不会涉及很高深的算法。今天,我就带你一块看下,如何利用简单的数据结构和算法,解决这种看似非常复杂的问题。
基于黑名单的过滤器
我们可以维护一个骚扰电话号码和垃圾短信发送号码的黑名单。这个黑名单的收集,有很多途径,比如,我们可以从一些公开的网站上下载,也可以通过类似“360 骚扰电话拦截”的功能,通过用户自主标记骚扰电话来收集。对于被多个用户标记,并且标记个数超过一定阈值的号码,我们就可以定义为骚扰电话,并将它加入到我们的黑名单中。
如果黑名单中的电话号码不多的话,我们可以使用散列表、二叉树等动态数据结构来存储,对内存的消耗并不会很大。如果我们把每个号码看作一个字符串,并且假设平均长度是 16 个字节,那存储 50 万个电话号码,大约需要 10MB 的内存空间。即便是对于手机这样的内存有限的设备来说,这点内存的消耗也是可以接受的。
但是,如果黑名单中的电话号码很多呢?比如有 500 万个。这个时候,如果再用散列表存储,就需要大约 100MB 的存储空间。为了实现一个拦截功能,耗费用户如此多的手机内存,这显然有点儿不合理。
上一节我们讲了,布隆过滤器最大的特点就是比较省存储空间,所以,用它来解决这个问题再合适不过了。如果我们要存储 500 万个手机号码,我们把位图大小设置为 10 倍数据大小,也就是 5000 万,那也只需要使用 5000 万个二进制位(5000 万 bits),换算成字节,也就是不到 7MB 的存储空间。比起散列表的解决方案,内存的消耗减少了很多。
不过,你可能还会说,布隆过滤器会有误判的概率呀!如果它把一个重要的电话或者短信,当成垃圾短信或者骚扰电话拦截了,对于用户来说,这是无法接受的。你说得没错,这是一个很大的问题。不过,我们现在先放一放,等三种过滤器都讲完之后,我再来解答。
实际上,我们还有一种时间换空间的方法,可以将内存的消耗优化到极致。
我们可以把黑名单存储在服务器端上,把过滤和拦截的核心工作,交给服务器端来做。手机端只负责将要检查的号码发送给服务器端,服务器端通过查黑名单,判断这个号码是否应该被拦截,并将结果返回给手机端。
用这个解决思路完全不需要占用手机内存。不过,有利就有弊。我们知道,网络通信是比较慢的,所以,网络延迟就会导致处理速度降低。而且,这个方案还有个硬性要求,那就是只有在联网的情况下,才能正常工作。
基于规则的过滤器
刚刚讲了一种基于黑名单的垃圾短信过滤方法,但是,如果某个垃圾短信发送者的号码并不在黑名单中,那这种方法就没办法拦截了。所以,基于黑名单的过滤方式,还不够完善,我们再继续看一种基于规则的过滤方式。
对于垃圾短信来说,我们还可以通过短信的内容,来判断某条短信是否是垃圾短信。我们预先设定一些规则,如果某条短信符合这些规则,我们就可以判定它是垃圾短信。实际上,规则可以有很多,比如下面这几个:
- 短信中包含特殊单词(或词语),比如一些非法、淫秽、反动词语等
- 短信发送号码是群发号码,非我们正常的手机号码,比如 +60389585
- 短信中包含回拨的联系方式,比如手机号码、微信、QQ、网页链接等,因为群发短信的号码一般都是无法回拨的
- 短信格式花哨、内容很长,比如包含各种表情、图片、网页链接等
- 符合已知垃圾短信的模板。垃圾短信一般都是重复群发,对于已经判定为垃圾短信的短信,我们可以抽象成模板,将获取到的短信与模板匹配,一旦匹配,我们就可以判定为垃圾短信
当然,如果短信只是满足其中一条规则,如果就判定为垃圾短信,那会存在比较大的误判的情况。我们可以综合多条规则进行判断。比如,满足 2 条以上才会被判定为垃圾短信;或者每条规则对应一个不同的得分,满足哪条规则,我们就累加对应的分数,某条短信的总得分超过某个阈值,才会被判定为垃圾短信。
不过,我只是给出了一些制定规则的思路,具体落实到执行层面,其实还有很大的距离,还有很多细节需要处理。比如,第一条规则中,我们该如何定义特殊单词;第二条规则中,我们该如何定义什么样的号码是群发号码等等。限于篇幅,我就不一一详细展开来讲了。我这里只讲一下,如何定义特殊单词?
如果我们只是自己拍脑袋想,哪些单词属于特殊单词,那势必有比较大的主观性,也很容易漏掉某些单词。实际上,我们可以基于概率统计的方法,借助计算机强大的计算能力,找出哪些单词最常出现在垃圾短信中,将这些最常出现的单词,作为特殊单词,用来过滤短信。
不过这种方法的前提是,我们有大量的样本数据,也就是说,要有大量的短信(比如 1000 万条短信),并且每条短信都做好了标记,它是垃圾短信还是非垃圾短信。
- 我们对这 1000 万条短信,进行分词处理(借助中文或者英文分词算法)
- 去掉“的、和、是”等没有意义的停用词(Stop words),得到 n 个不同的单词
- 针对每个单词,统计有多少个垃圾短信出现了这个单词,有多少个非垃圾短信会出现这个单词
- 求出每个单词出现在垃圾短信中的概率,以及出现在非垃圾短信中的概率
- 如果某个单词出现在垃圾短信中的概率,远大于出现在非垃圾短信中的概率,那我们就把这个单词作为特殊单词,用来过滤垃圾短信
基于概率统计的过滤器
基于规则的过滤器,看起来很直观,也很好理解,但是它也有一定的局限性。
- 一方面,这些规则受人的思维方式局限,规则未免太过简单
- 另一方面,垃圾短信发送者可能会针对规则,精心设计短信,绕过这些规则的拦截
对此,我们再来看一种更加高级的过滤方式,基于概率统计的过滤方式。
什么是朴素贝叶斯算法
这种基于概率统计的过滤方式,基础理论是基于朴素贝叶斯算法。为了让你更好地理解下面的内容,我们先通过一个非常简单的例子来看下,什么是朴素贝叶斯算法?
假设事件 A 是“小明不去上学”,事件 B 是“下雨了”。我们现在统计了一下过去 10 天的下雨情况和小明上学的情况,作为样本数据。
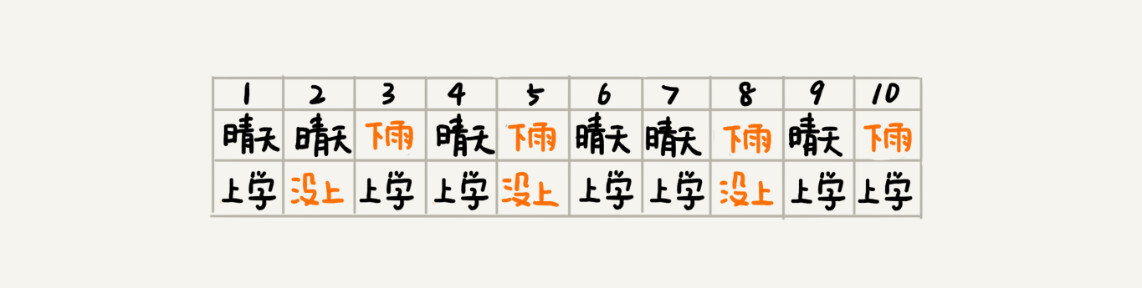
我们来分析一下,这组样本有什么规律。
- 在这 10 天中,有 4 天下雨,所以下雨的概率 P(B) = 4/10
- 10 天中小明有 3 天没有去上学,所以小明不去上学的概率 P(A) = 3/10
- 在 4 个下雨天中,小明有 2 天没去上学,所以下雨天不去上学的概率 P(A|B) = 2/4
- 在小明没有去上学的 3 天中,有 2 天下雨了,所以小明因为下雨而不上学的概率是 P(B|A) = 2/3
实际上,这 4 个概率值之间,有一定的关系,这个关系就是朴素贝叶斯算法,我们用公式表示出来,就是下面这个样子。
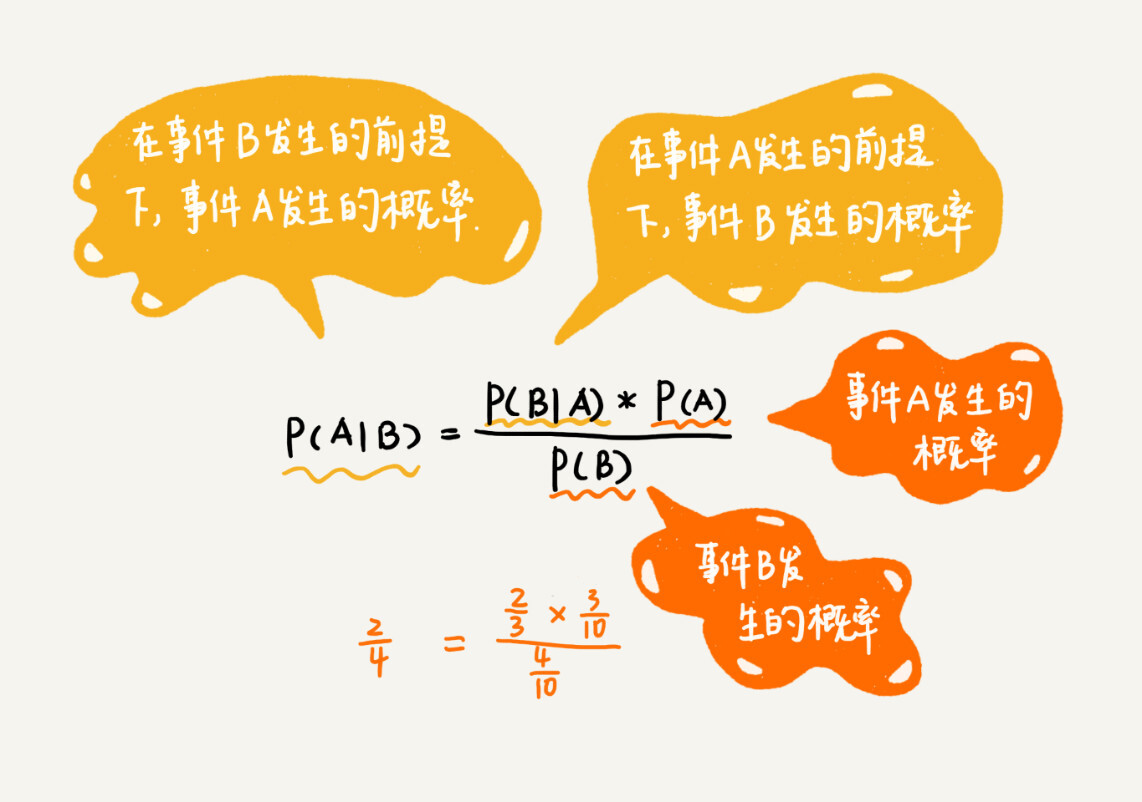
贝叶斯定理:P(A|B) = P(B|A) * P(A) / P(B)
如何用来做垃圾短信的过滤
弄懂了朴素贝叶斯算法,我们再回到垃圾短信过滤这个问题上,看看如何利用朴素贝叶斯算法,来做垃圾短信的过滤。
基于概率统计的过滤器,是基于短信内容来判定是否是垃圾短信。而计算机没办法像人一样理解短信的含义。所以,我们需要把短信抽象成一组计算机可以理解并且方便计算的特征项,用这一组特征项代替短信本身,来做垃圾短信过滤。
我们可以通过分词算法,把一个短信分割成 n 个单词。这 n 个单词就是一组特征项,全权代表这个短信。因此,判定一个短信是否是垃圾短信这样一个问题,就变成了,判定同时包含这几个单词的短信是否是垃圾短信。
不过,这里我们并不像基于规则的过滤器那样,非黑即白,一个短信要么被判定为垃圾短信、要么被判定为非垃圾短息。我们使用概率来表征一个短信是垃圾短信的可信程度。如果我们用公式将这个概率表示出来,就是下面这个样子:
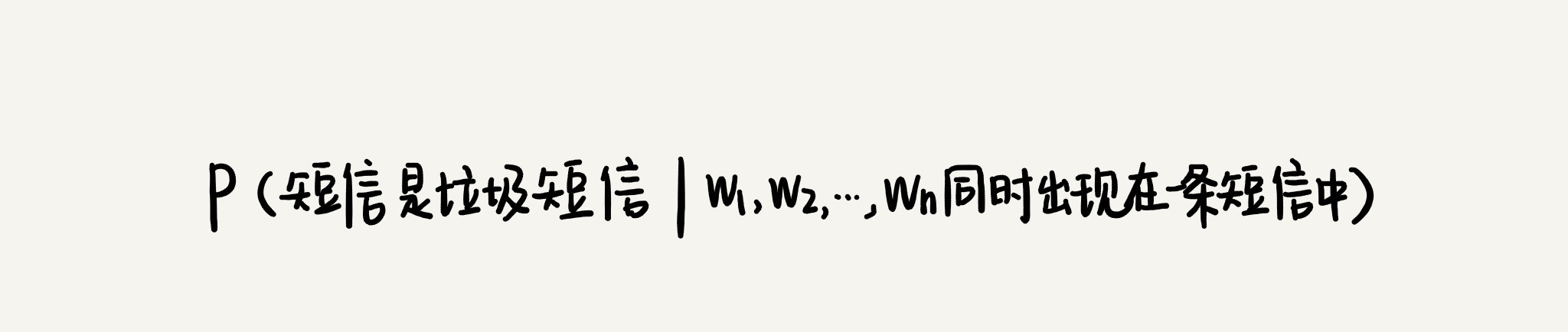
尽管我们有大量的短信样本,但是我们没法通过样本数据统计得到这个概率。为什么不可以呢?你可能会说,我只需要统计同时包含 W1,W2,W3,…,Wn 这 n 个单词的短信有多少个(我们假设有 x 个),然后看这里面属于垃圾短信的有几个(我们假设有 y 个),那包含 W1,W2,W3,…,Wn 这 n 个单词的短信是垃圾短信的概率就是 y/x。
理想很丰满,但现实往往很骨感。你忽视了非常重要的一点,那就是样本的数量再大,毕竟也是有限的,样本中不会有太多同时包含 W1,W2,W3,…,Wn 的短信的,甚至很多时候,样本中根本不存在这样的短信。没有样本,也就无法计算概率。所以这样的推理方式虽然正确,但是实践中并不好用。
朴素贝叶斯公式
这个时候,朴素贝叶斯公式就可以派上用场了。
P(A|B) = P(B|A) * P(A) / P(B)
我们通过朴素贝叶斯公式,将这个概率的求解,分解为其他三个概率的求解。

那转化之后的三个概率是否可以通过样本统计得到呢?
P(W1,W2,W3,…,Wn 同时出现在一条短信中 | 短信是垃圾短信)这个概率照样无法通过样本来统计得到。但是我们可以基于下面这条著名的概率规则来计算。
独立事件发生的概率:P(A*B) = P(A) * P(B)
如果事件 A 和事件 B 是独立事件,两者的发生没有相关性,事件 A 发生的概率 P(A) 等于 p1,事件 B 发生的概率 P(B) 等于 p2,那两个同时发生的概率 P(A*B) = P(A) * P(B)。
基于这条独立事件发生概率的计算公式,我们可以把 P(W1,W2,W3,…,Wn 同时出现在一条短信中 | 短信是垃圾短信)分解为下面这个公式:

其中,P(Wi 出现在短信中 | 短信是垃圾短信)表示垃圾短信中包含 Wi 这个单词的概率有多大。这个概率值通过统计样本很容易就能获得。我们假设垃圾短信有 y 个,其中包含 Wi 的有 x 个,那这个概率值就等于 x/y。
我们再来看下剩下两个概率。
P(短信是垃圾短信)表示短信是垃圾短信的概率,这个很容易得到。我们把样本中垃圾短信的个数除以总样本短信个数,就是短信是垃圾短信的概率。
不过,P(W1,W2,W3,…,Wn 同时出现在一条短信中)这个概率还是不好通过样本统计得到,原因我们前面说过了,样本空间有限。不过,我们没必要非得计算这一部分的概率值。为什么这么说呢?
实际上,我们可以分别计算同时包含 W1,W2,W3,…,Wn 这 n 个单词的短信,是垃圾短信和非垃圾短信的概率。假设它们分别是 p1 和 p2。我们并不需要单纯地基于 p1 值的大小来判断是否是垃圾短信,而是通过对比 p1 和 p2 值的大小,来判断一条短信是否是垃圾短信。更细化一点讲,那就是,如果 p1 是 p2 的很多倍(比如 10 倍),我们才确信这条短信是垃圾短信。

基于这两个概率的倍数来判断是否是垃圾短信的方法,我们就可以不用计算 P(W1,W2,W3,…,Wn 同时出现在一条短信中)这一部分的值了,因为计算 p1 与 p2 的时候,都会包含这个概率值的计算,所以在求解 p1 和 p2 倍数 p1/p2 的时候,我们也就不需要这个值。
总结引申
今天,我们讲了基于黑名单、规则、概率统计三种垃圾短信的过滤方法,实际上,今天讲的这三种方法,还可以应用到很多类似的过滤、拦截的领域,比如垃圾邮件的过滤等等。
在讲黑名单过滤的时候,我讲到布隆过滤器可能会存在误判情况,可能会导致用户投诉。实际上,我们可以结合三种不同的过滤方式的结果,对同一个短信处理,如果三者都表明这个短信是垃圾短信,我们才把它当作垃圾短信拦截过滤,这样就会更精准。
当然,在实际的工程中,我们还需要结合具体的场景,以及大量的实验,不断去调整策略,权衡垃圾短信判定的准确率(是否会把不是垃圾的短信错判为垃圾短信)和召回率(是否能把所有的垃圾短信都找到),来实现我们的需求。
47 | 向量空间
如何实现一个简单的音乐推荐系统
很多音乐 App 都可以根据你听歌的口味偏好,给你推荐可能会喜爱的音乐,这个功能是怎么实现的呢?
解决思路的核心思想非常简单、直白,用两句话就能总结出来:
- 找到跟你口味偏好相似的用户,把他们爱听的歌曲推荐给你
- 找出跟你喜爱的歌曲特征相似的歌曲,把这些歌曲推荐给你
接下来,我就分别讲解一下这两种思路的具体实现方法。
基于相似用户做推荐
如何找到跟你口味偏好相似的用户呢?或者说如何定义口味偏好相似呢?
基于共同喜爱的歌曲数量
实际上,思路也很简单,我们把跟你听类似歌曲的人,看作口味相似的用户。你可以看我下面画的这个图。我用“1”表示“喜爱”,用“0”笼统地表示“不发表意见”。从图中我们可以看出,你跟小明共同喜爱的歌曲最多,有 5 首。于是,我们就可以说,小明跟你的口味非常相似。
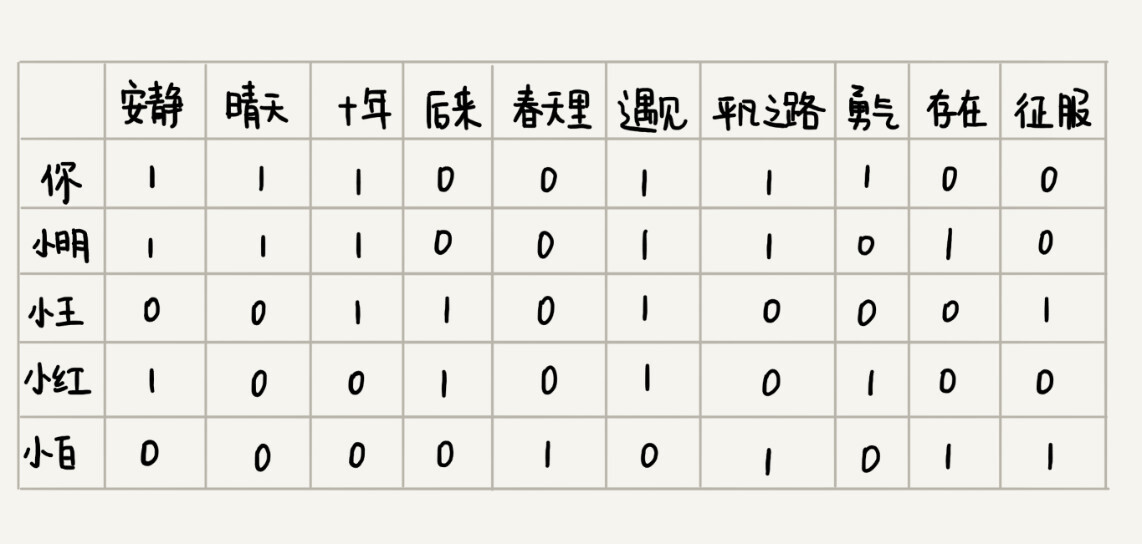
我们只需要遍历所有的用户,对比每个用户跟你共同喜爱的歌曲个数,并且设置一个阈值,如果你和某个用户共同喜爱的歌曲个数超过这个阈值,我们就把这个用户看作跟你口味相似的用户,把这个用户喜爱但你还没听过的歌曲,推荐给你。
基于用户对相同歌曲的行为
不过,我们如何知道用户喜爱哪首歌曲呢?也就是说,如何定义用户对某首歌曲的喜爱程度呢?
实际上,我们可以通过用户的行为,来定义这个喜爱程度。我们给每个行为定义一个得分,得分越高表示喜爱程度越高。

还是刚刚那个例子,我们如果把每个人对每首歌曲的喜爱程度表示出来,就是下面这个样子。图中,某个人对某首歌曲是否喜爱,我们不再用“1”或者“0”来表示,而是对应一个具体的分值。
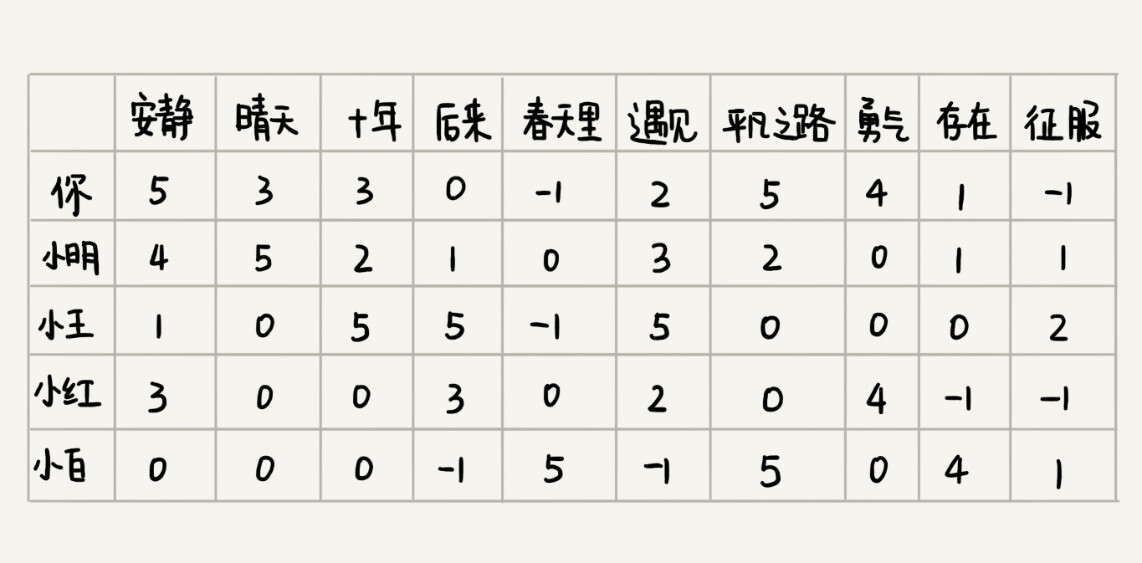
基于向量间的欧几里得距离
欧几里得距离 Euclidean distance
向量 Vector
有了这样一个用户对歌曲的喜爱程度的对应表之后,如何来判断两个用户是否口味相似呢?
显然,我们不能再像之前那样,采用简单的计数来统计两个用户之间的相似度。还记得我们之前讲字符串相似度度量时,提到的编辑距离吗?这里的相似度度量,我们可以使用另外一个距离,那就是欧几里得距离。
欧几里得距离是用来计算两个向量之间的距离的。这个概念中有两个关键词,向量和距离,我来给你解释一下。
- 一维空间是一条线,我们用 1,2,3…… 这样单个的数,来表示一维空间中的某个位置
- 二维空间是一个面,我们用(1,3)(4,2)(2,2)…… 这样的两个数,来表示二维空间中的某个位置
- 三维空间是一个立体空间,我们用(1,3,5)(3,1,7)(2,4,3)…… 这样的三个数,来表示三维空间中的某个位置
- 类比到 K 维空间中,我们可以用(X1,X2,X3,…,XK)这样的 K 个数,来表示 K 维空间中的某个位置
这种表示方法就是向量(vector)。我们知道,二维、三维空间中,两个位置之间有距离的概念,类比到高纬空间,同样也有距离的概念,这就是我们说的两个向量之间的距离。
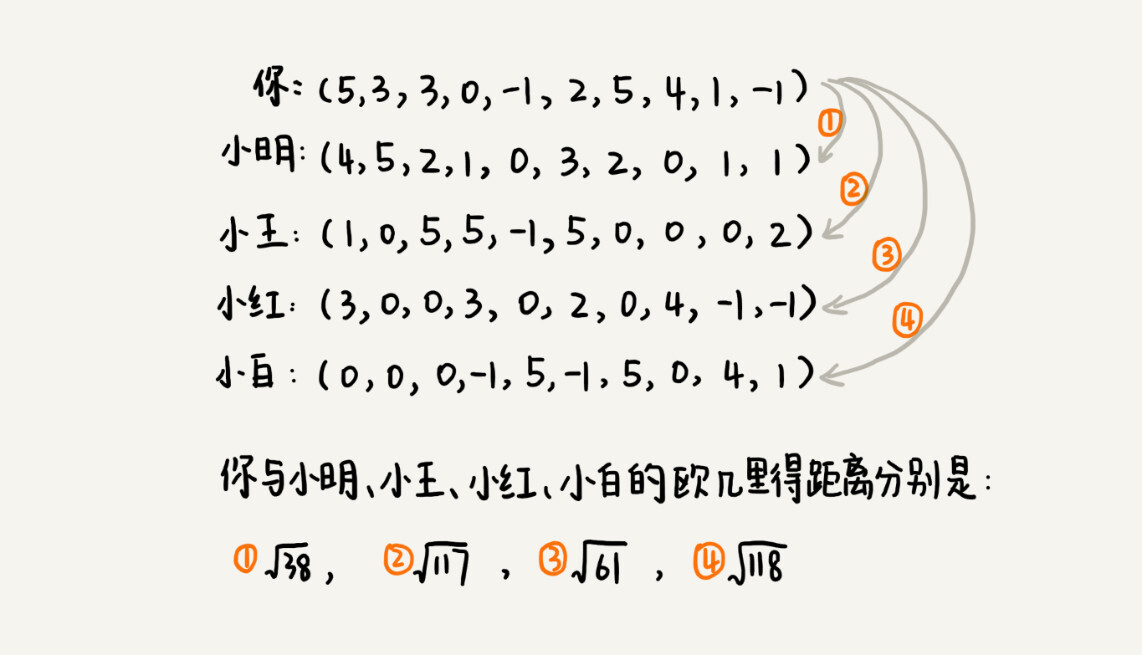
那如何计算两个向量之间的距离呢?这个就是欧几里得距离的计算公式:

我们把每个用户对所有歌曲的喜爱程度,都用一个向量表示。我们计算出两个向量之间的欧几里得距离,作为两个用户的口味相似程度的度量。从图中的计算可以看出,小明与你的欧几里得距离距离最小,也就是说,你俩在高维空间中靠得最近,所以,我们就断定,小明跟你的口味最相似。
基于相似歌曲做推荐
刚刚我们讲了基于相似用户的歌曲推荐方法,现在再来看另外一种推荐方法,基于相似歌曲的推荐方法,也就是说,如果某首歌曲跟你喜爱的歌曲相似,我们就把它推荐给你。
如何判断两首歌曲是否相似呢?对于人来说,这个事情可能会比较简单,但是对于计算机来说,判断两首歌曲是否相似,那就需要通过量化的数据来表示了。我们应该通过什么数据来量化两个歌曲之间的相似程度呢?
最容易想到的是,我们对歌曲定义一些特征项,比如是伤感的还是愉快的,是摇滚还是民谣,是柔和的还是高亢的等等。类似基于相似用户的推荐方法,我们给每个歌曲的每个特征项打一个分数,这样每个歌曲就都对应一个特征项向量。我们可以基于这个特征项向量,来计算两个歌曲之间的欧几里得距离。欧几里得距离越小,表示两个歌曲的相似程度越大。
但是,要实现这个方案,需要有一个前提,那就是我们能够找到足够多,并且能够全面代表歌曲特点的特征项,除此之外,我们还要人工给每首歌标注每个特征项的得分。对于收录了海量歌曲的音乐 App 来说,这显然是一个非常大的工程。此外,人工标注有很大的主观性,也会影响到推荐的准确性。
既然基于歌曲特征项计算相似度不可行,那我们就换一种思路。对于两首歌,如果喜欢听的人群都是差不多的,那侧面就可以反映出,这两首歌比较相似。如图所示,每个用户对歌曲有不同的喜爱程度,我们依旧通过上一个解决方案中定义得分的标准,来定义喜爱程度。
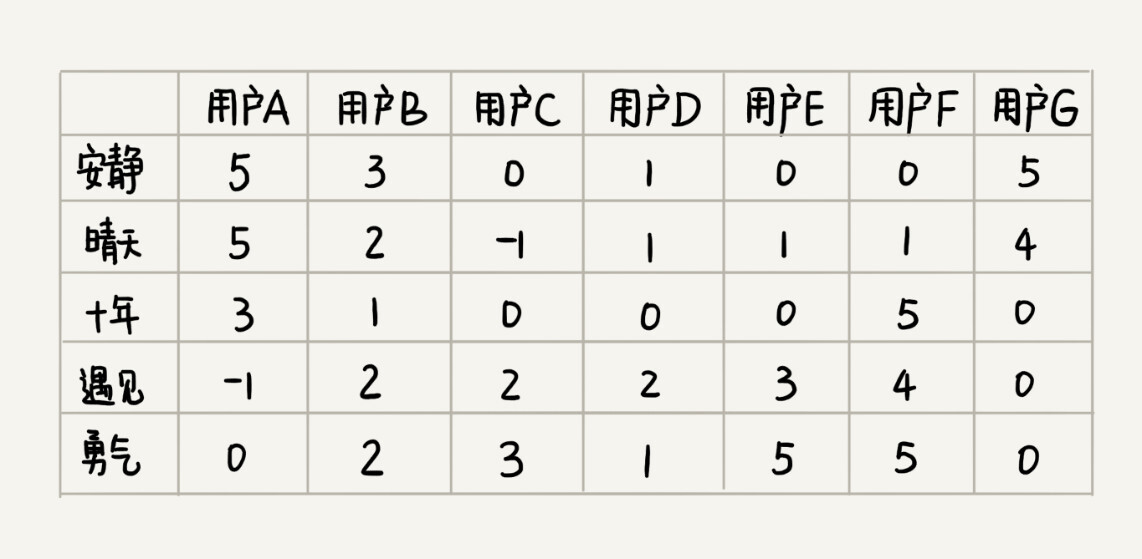
你有没有发现,这个图跟基于相似用户推荐中的图几乎一样。只不过这里把歌曲和用户主次颠倒了一下。
- 基于相似用户的推荐方法中,针对每个用户,我们将对各个歌曲的
喜爱程度作为向量 - 基于相似歌曲的推荐思路中,针对每个歌曲,我们将每个用户的
打分作为向量
有了每个歌曲的向量表示,我们通过计算向量之间的欧几里得距离,来表示歌曲之间的相似度。欧几里得距离越小,表示两个歌曲越相似。然后,我们就在用户已经听过的歌曲中,找出他喜爱程度较高的歌曲。然后,我们找出跟这些歌曲相似度很高的其他歌曲,推荐给他。
总结引申
实际上,这个问题是推荐系统(Recommendation System)里最典型的一类问题。之所以讲这部分内容,主要还是想给你展示算法的强大之处,利用简单的向量空间的欧几里得距离,就能解决如此复杂的问题。不过,今天,我只给你讲解了基本的理论,实践中遇到的问题还有很多,比如冷启动问题,产品初期积累的数据不多,不足以做推荐等等。这些更加深奥的内容,你可以之后自己在实践中慢慢探索。
2017-04-02
本文来自博客园,作者:白乾涛,转载请注明原文链接:https://www.cnblogs.com/baiqiantao/p/6658008.html



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现