数据结构与算法之美-13 贪心 分治 回溯

本文地址

---

目录

目录

• 目录
• 37 | 贪心算法
  • 贪心算法介绍
  • 贪心算法的局限性
  • 贪心算法案例
    • 分糖果
    • 钱币找零
    • 区间覆盖
    • 移除数字
  • 霍夫曼编码
    • 设计思想
    • 编码过程
    • 另一个案例
• 38 | 分治算法
  • 如何理解分治算法
  • 分治算法的应用
    • 如何计算逆序度
    • 海量数据处理
    • MapReduce 的本质
• 39 | 回溯算法
  • 如何理解回溯算法
  • 回溯算法的应用
    • 八皇后问题
    • 0-1 背包问题
    • 正则表达式匹配

37 | 贪心算法

接下来几节会讲 4 个算法思想，包括贪心、分治、回溯、动态规划。他们虽然不是具体的算法，但是常用来指导我们设计具体的算法和编码。

贪心算法 Greedy Algorithm 有很多经典的应用

• 霍夫曼编码 Huffman Coding
• Prim 和 Kruskal 最小生成树算法
• Dijkstra 单源最短路径算法

实际上，贪心算法适用的场景比较有限，这种算法思想更多的是指导设计基础算法。

贪心算法的最难的一块是如何将要解决的问题抽象成贪心算法模型，只要这一步搞定之后，贪心算法的编码一般都很简单。贪心算法解决问题的正确性虽然很多时候都看起来是显而易见的，但是要严谨地证明算法能够得到最优解，并不是件容易的事。所以，很多时候，我们只需要多举几个例子，看一下贪心算法的解决方案是否真的能得到最优解就可以了。

贪心算法介绍

先看一个非常简单的案例：假设我们有一个可以容纳 100kg 物品的背包，可以装以下 5 种豆子，每种豆子的总量和总价值都各不相同。为了让背包中所装物品的总价值最大，如何选择在背包中装哪些豆子，以及每种豆子装多少？

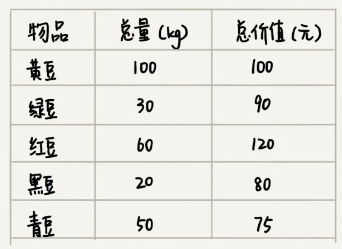
实际上，这个问题很简单，我们只要先算一算每个物品的单价，按照单价由高到低依次来装就好了。单价从高到低排列依次是：黑豆、绿豆、红豆、青豆、黄豆。所以，我们可以往背包里装 20kg 黑豆、30kg 绿豆、50kg 红豆。

这个问题的解决思路显而易见，然而本质上它借助的就是贪心算法。

使用贪心算法解决问题的步骤：

• 首先要联想到是否符合贪心算法的基本框架
  • 针对一组数据，定义了限制值和期望值，希望从中选出几个数据，在满足限制值的情况下，期望值最大
• 然后尝试看下这个问题是否可以用贪心算法解决
  • 每次都选择在对限制值同等贡献量的情况下，对期望值贡献最大的数据
• 最后举几个例子看下贪心算法产生的结果是否是最优的
  • 大部分情况下，举几个例子验证一下就可以了，严格地证明贪心算法的正确性是非常复杂的。

贪心算法的局限性

实际上，用贪心算法的思路解决问题，往往不总能给出最优解。

比如，在一个有权图中，从顶点 S 开始，找一条到顶点 T 的最短路径（路径中边的权值和最小）。贪心算法的解决思路是，每次都选择一条跟当前顶点相连的权最小的边，直到找到顶点 T。按照这种思路求出的最短路径是 S -> A -> E -> T，路径长度是 1 + 4 + 4 = 9。

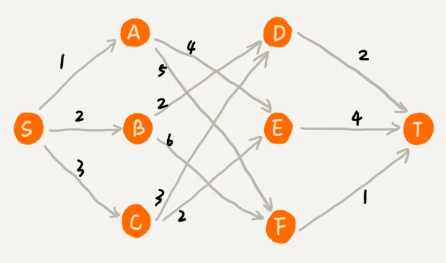
但是，这种方式最终求的路径并不是最短路径，为什么用贪心算法解决这个问题不行呢？

在这个问题上，贪心算法不工作的主要原因是，前面的选择，会影响后面的选择。换句话说就是，局部最优并不能保证也是全局最优。

如果我们第一步从顶点 S 走到顶点 A，那接下来面对的顶点和边，跟第一步从顶点 S 走到顶点 B，是完全不同的。所以，即便我们第一步选择最优的走法，但有可能因为这一步选择，导致后面每一步的选择都很糟糕，最终也就无缘全局最优解了。

贪心算法案例

掌握贪心算法的关键是多练习，只要多练习几道题，自然就有感觉了。

分糖果

假设有 m 个糖果和 n 个孩子，现在要把糖果分给这些孩子，但是糖果少孩子多(n < m)，所以糖果只能分配给一部分孩子(并且每个孩子最多只能分一个糖果)。

每个糖果的大小不等，这 m 个糖果的大小分别是 `s1，s2，s3，……，sm`。每个孩子对糖果大小的需求也不一样，只有糖果的大小大于等于孩子的对糖果大小的需求的时候，孩子才得到满足。假设这 n 个孩子对糖果大小的需求分别是 `g1，g2，g3，……，gn`。

问题：如何分配糖果，才可以尽可能满足最多数量的孩子？

这个问题的限制值就是糖果的个数 m，期望值是 n 个孩子中被满足的孩子的个数。

用贪心算法解决问题的思路：

• 对于一个孩子来说，如果小的糖果可以满足，就没必要用更大的糖果，这样更大的就可以留给其他对糖果大小需求更大的孩子
• 由于满足一个需求大的孩子跟满足一个需求小的孩子对我们期望值的贡献是一样的，同时由于需求小的孩子更容易被满足，所以，我们应该从需求小的孩子开始分配糖果

简单来说就是：从小到大排序并遍历 g1，g2，g3，……，gn，每次给剩下的孩子中对糖果大小需求最小的孩子，发给他剩下的糖果中能满足他的最小的糖果。

另外一种思路好像也可以：从大到小排序并排序并遍历 s1，s2，s3，……，sm，每次将剩下的最大的糖果，分给对糖果大小需求最大、且能被满足的孩子。

钱币找零

假设我们有 1 元、2 元、5 元、10 元、20 元、50 元、100 元这些面额的纸币，它们的张数分别是 c1、c2、c5、c10、c20、c50、c100。

问题：我们现在要用这些钱来支付 K 元，最少要用多少张纸币呢？

这个问题的限制值是总金额，期望值是纸币数量。

在生活中，我们肯定是先用面值最大的来支付，如果不够，就继续用更小一点面值的，以此类推，最后剩下的用 1 元来补齐。

在贡献相同期望值（纸币数量）的情况下，我们希望多贡献点金额，这样就可以让纸币数更少，这就是一种贪心算法的解决思路。直觉告诉我们，这种处理方法就是最好的。但是要严谨地证明这种贪心算法的正确性，需要比较复杂的、有技巧的数学推导，如果感兴趣的话可以自己去研究下。

区间覆盖

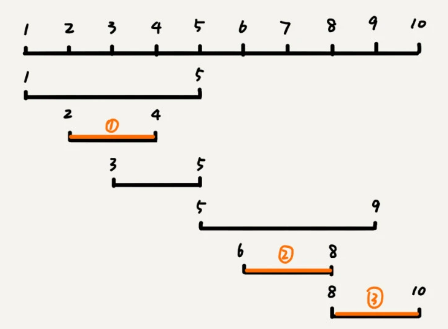
假设我们有 n 个区间，区间的起始端点和结束端点分别是[l1, r1]，[l2, r2]，[l3, r3]，……，[ln, rn]。

问题：从这 n 个区间中选出一部分区间，这部分区间满足两两不相交，最多能选出多少个区间？

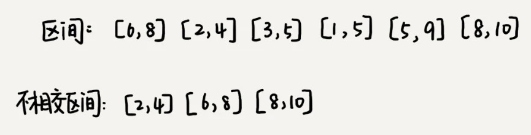
这个问题的处理思路稍微不是那么好懂，不过，我建议你最好能弄懂，因为这个处理思想在很多贪心算法问题中都有用到，比如任务调度、教师排课等等问题。

这个问题的解决思路是这样的：

• 先按照起始端点从小到大的顺序对这 n 个区间排序
• 每次选择【左端点跟前面的已经覆盖的区间不重合的】、【右端点又尽量小的】区间，这样可以让剩下的未覆盖区间尽可能的大，就可以放置更多的区间

说起来简单，实际上代码并没那么好写。

移除数字

在一个非负整数 a 中，从中移除 k 个数字，让剩下的数字值最小，如何选择移除哪 k 个数字呢？

345678
876543
348765
321876
325186

• CASE A：从左往右遍历 a，如果发现存在相邻的两位数，左边大于右边，则删除左边的数
• 如果遍历完发现不存在 CASE A，则删除最后一位
• 递归遍历 k 次即可

霍夫曼编码

假设有一个包含 1000 个字符的文件，如果每个字符占 1 个 byte（1byte = 8bits），存储这 1000 个字符就一共需要 8000bits，有没有更加节省空间的存储方式呢？

假设我们通过统计分析发现，这 1000 个字符中只包含 6 种不同字符，假设它们分别是 a、b、c、d、e、f。而 3 个二进制位（bit）就可以表示 8 个不同的字符，所以，为了尽量减少存储空间，每个字符我们用 3 个二进制位来表示。那存储这 1000 个字符只需要 3000bits 就可以了。

还有没有更加节省空间的存储方式呢？

霍夫曼编码就要登场了。霍夫曼编码是一种十分有效的编码方法，广泛用于数据压缩中，其压缩率通常在 20%～90% 之间。

设计思想

霍夫曼编码不仅会考察文本中有多少个不同字符，还会考察每个字符出现的频率，根据频率的不同，选择不同长度的编码。霍夫曼编码试图用这种不等长的编码方法，来进一步增加压缩的效率。

如何给不同频率的字符选择不同长度的编码呢？根据贪心的思想，我们可以把出现频率比较多的字符，用稍微短一些的编码；出现频率比较少的字符，用稍微长一些的编码。

等长的编码解压缩起来很简单。比如刚才那个例子中，我们用 3 个 bit 表示一个字符。在解压缩的时候，我们每次从文本中读取 3 位二进制码，然后翻译成对应的字符。但是，霍夫曼编码是不等长的，每次应该读取 1 位还是 2 位、3 位等等来解压缩呢？这个问题就导致霍夫曼编码解压缩起来比较复杂。为了避免解压缩过程中的歧义，霍夫曼编码要求各个字符的编码之间，不会出现某个编码是另一个编码前缀的情况。

假设这 6 个字符出现的频率从高到低依次是 a、b、c、d、e、f。我们把它们编码下面这个样子，任何一个字符的编码都不是另一个的前缀，在解压缩的时候，每次会读取尽可能长的可解压的二进制串，所以在解压缩的时候也不会歧义。经过这种编码压缩之后，这 1000 个字符只需要 2100bits 就可以了。

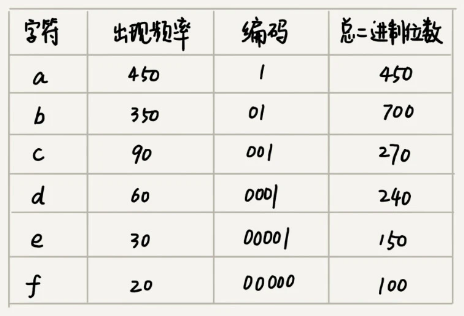
编码过程

尽管霍夫曼编码的思想并不难理解，但是如何根据字符出现频率的不同，给不同的字符进行不同长度的编码呢？

目标：通过遍历优先级队列，构造一颗哈夫曼树

• 首先要构建一个优先级队列
  • 注意：这里使用的不是普通的队列(先进先出)，也不是栈(后进先出)，而是优先级队列
  • 这里的优先级队列的特性是：不管入队列的顺序是什么，都是频率最小的元素先出队
• 从队列中取出频率最小的两个节点 A、B (简单的出队就可以了)
• 然后新建一个节点 C，把频率设置为两个节点的频率之和，并把这个新节点 C 作为节点 A、B 的父节点
• 最后再把 C 节点放入到优先级队列中
• 重复这个过程，直到队列中没有数据
  • 下图中，上次创建的父节点都会在下次遍历时出队，实际上，这只是巧合

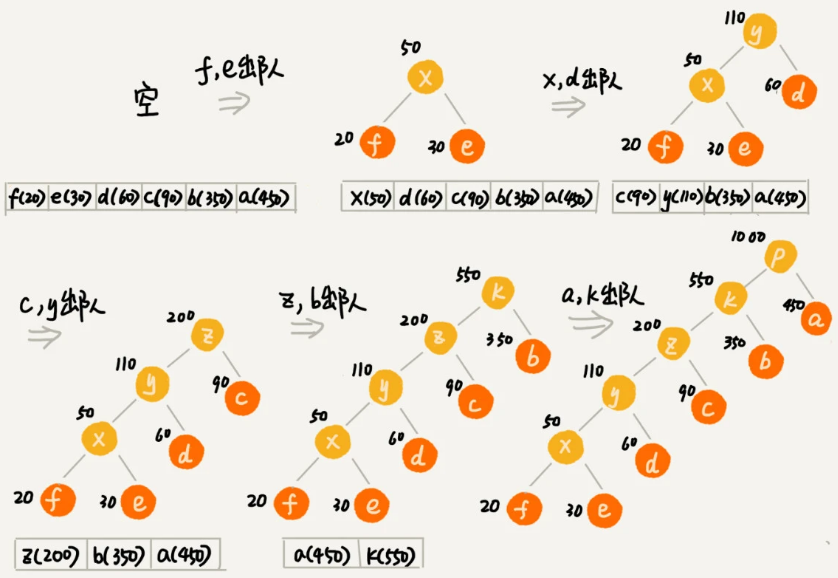
现在，我们给每一条边加上画一个权值，指向左子节点的边统统标记为 0，指向右子节点的边统统标记为 1，那从根节点到叶节点的路径就是叶节点对应字符的霍夫曼编码。

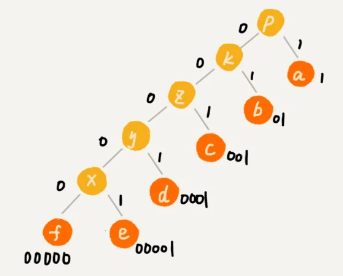
另一个案例

假如有 A、B、C、D、E 五个字符，出现的频率(权值)分别为5、4、3、2、1，那么构建哈夫曼树的过程如下：

• 先从权值集合{5,4,3,2,1}中取出两个最小的权值 1、2
• 然后创建一个新节点作为其父节点，新父点的权值为 1+2=3
• 把新生成的权值为 3 的父点放到的集合中，所以集合变成了{5,4,3,3}
• 重复上面的操作直到集合为空

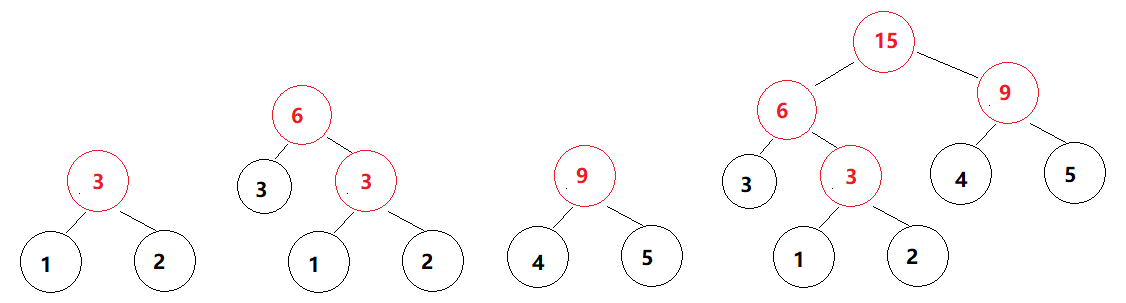
将各个权值替换为对应的字符后即为下图

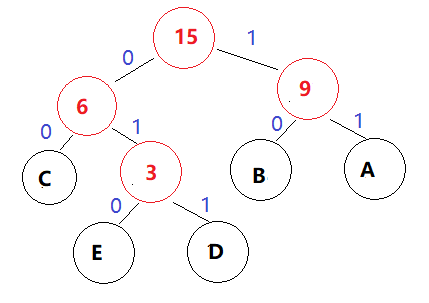
所以各字符对应的编码为：A->11，B->10，C->00，D->011，E->010

38 | 分治算法

如何理解分治算法

分治算法（divide and conquer）的核心思想就是分而治之 ，也就是将原问题划分成 n 个规模较小，并且结构与原问题相似的子问题，递归地解决这些子问题，然后再合并其结果，就得到原问题的解。

分治算法一般都比较适合用递归来实现。分治算法是一种处理问题的思想，递归是一种编程技巧。

分治算法的递归实现中，每一层递归都会涉及这样三个操作：

• 分解：将原问题分解成一系列子问题
• 解决：递归地求解各个子问题，若子问题足够小，则直接求解
• 合并：将子问题的结果合并成原问题

分治算法能解决的问题，一般需要满足下面这几个条件：

• 原问题与分解成的小问题具有相同的模式
• 原问题分解成的子问题可以独立求解，子问题之间没有相关性，这一点是分治算法跟动态规划的明显区别
• 具有分解终止条件，也就是说，当问题足够小时，可以直接求解
• 可以将子问题合并成原问题，并且这个合并操作的复杂度不能太高

分治算法的应用

如何计算逆序度

在排序算法里，我们用有序度来表示一组数据的有序程度，用逆序度表示一组数据的无序程度。

假设有 n 个数据，我们期望数据从小到大排列

• 完全有序的数据的有序度就是 n(n-1)/2，逆序度等于 0
• 倒序排列的数据的有序度就是 0，逆序度是 n(n-1)/2
• 除了这两种极端情况外，我们通过计算有序对或者逆序对的个数，来表示数据的有序度或逆序度

现在的问题是，如何求出一组数据的有序对个数或者逆序对个数呢？

最笨的方法是，拿每个数字跟它后面的数字比较，看有几个比它小的。我们把比它小的数字个数记作 k，通过这样的方式，把每个数字都考察一遍之后，然后对每个数字对应的 k 值求和，最后得到的总和就是逆序对个数。不过，这样操作的时间复杂度是 O(n^2)。有没有更加高效的处理方法呢？

我们用分治算法来试试。我们套用分治的思想来求数组 A 的逆序对个数。我们可以将数组分成前后两半 A1 和 A2，分别计算 A1 和 A2 的逆序对个数 K1 和 K2，然后再计算 A1 与 A2 之间的逆序对个数 K3。那数组 A 的逆序对个数就等于 K1 + K2 + K3。

使用分治算法其中一个要求是，子问题合并的代价不能太大，否则就起不了降低时间复杂度的效果了，如何快速计算出两个子问题 A1 与 A2 之间的逆序对个数呢？

这里就要借助归并排序算法了。

归并排序中有一个非常关键的操作，就是将两个有序的小数组，合并成一个有序的数组。实际上，在这个合并的过程中，我们就可以计算这两个小数组的逆序对个数了。每次合并操作，我们都计算逆序对个数，把这些计算出来的逆序对个数求和，就是这个数组的逆序对个数了。

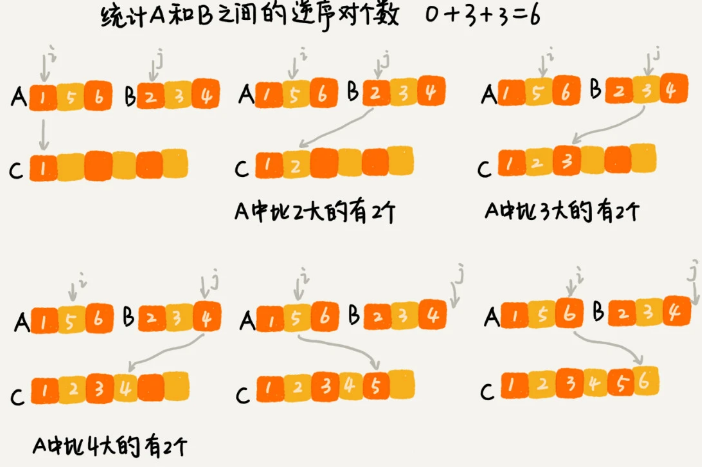
private int num = 0; // 全局变量或者成员变量

public int count(int[] a, int n) {
  num = 0;
  mergeSortCounting(a, 0, n-1);
  return num;
}

private void mergeSortCounting(int[] a, int p, int r) {
  if (p >= r) return;
  int q = (p+r)/2;
  mergeSortCounting(a, p, q);
  mergeSortCounting(a, q+1, r);
  merge(a, p, q, r);
}

private void merge(int[] a, int p, int q, int r) {
  int i = p, j = q+1, k = 0;
  int[] tmp = new int[r-p+1];
  while (i<=q && j<=r) {
    if (a[i] <= a[j]) {
      tmp[k++] = a[i++];
    } else {
      num += (q-i+1); // 统计p-q之间，比a[j]大的元素个数
      tmp[k++] = a[j++];
    }
  }
  while (i <= q) { // 处理剩下的
    tmp[k++] = a[i++];
  }
  while (j <= r) { // 处理剩下的
    tmp[k++] = a[j++];
  }
  for (i = 0; i <= r-p; ++i) { // 从tmp拷贝回a
    a[p+i] = tmp[i];
  }
}

海量数据处理

分治算法思想的应用是非常广泛的，并不仅限于指导编程和算法设计。它还经常用在海量数据处理的场景中。

我们前面讲的数据结构和算法，大部分都是基于内存存储和单机处理。但是，如果要处理的数据量非常大，没法一次性放到内存中，这个时候，这些数据结构和算法就无法工作了。

比如，给 10GB 的订单文件按照金额排序这样一个需求，看似是一个简单的排序问题，但是因为数据量大，无法一次性加载到内存，也就无法通过单纯地使用快排、归并等基础算法来解决了。

要解决这种数据量大到内存装不下的问题，我们就可以利用分治的思想。我们可以将海量的数据集合根据某种方法，划分为几个小的数据集合，每个小的数据集合单独加载到内存来解决，然后再将小数据集合合并成大数据集合。实际上，利用这种分治的处理思路，不仅仅能克服内存的限制，还能利用多线程或者多机处理，加快处理的速度。

比如刚刚举的那个例子，给 10GB 的订单排序，我们就可以先扫描一遍订单，根据订单的金额，将 10GB 的文件划分为几个金额区间。比如订单金额为 1 到 100 元的放到一个小文件，101 到 200 之间的放到另一个文件，以此类推。这样每个小文件都可以单独加载到内存排序，最后将这些有序的小文件合并，就是最终有序的 10GB 订单数据了。

这不就是桶排序吗

如果订单数据存储在类似 GFS 这样的分布式系统上，当 10GB 的订单被划分成多个小文件的时候，每个文件可以并行加载到多台机器上处理，最后再将结果合并在一起，这样并行处理的速度也加快了很多。

你可能还有印象，这个就是我在讲线性排序的时候举的例子。实际上，在前面已经学习的课程中，我还讲了很多利用分治思想来解决的问题。

MapReduce 的本质

MapReduce、GFS、Bigtable 是 Google 大数据处理的三驾马车。

• MapReduce 是一个处理大数据集的编程模型，它通过 map 函数把基于行的输入转化成不同的键值对，再通过 reduce 函数把这些键值对针对相同的键进行聚合，并在聚合的过程中进行相应的计算
• GFS 是一个分布式文件系统，用来存储大量的较大文件，它可以在廉价的硬件上实现存储文件，并做到容错性，并且针对多个客户同时访问提供比较有竞争力的性能
• Bigtable 是一个可以管理结构化数据的分布式存储系统，它本身支持水平的横向扩展，通过使用成千上万的连接服务器，来支持 PB 量级的数据处理
  • Borg 是谷歌内部的大规模集群管理系统

我们刚刚举的订单的例子，数据有 10GB 大小，可能给你的感受还不强烈。那如果我们要处理的数据是 1T、10T、100T 这样子的，那一台机器处理的效率肯定是非常低的。而对于谷歌搜索引擎来说，网页爬取、清洗、分析、分词、计算权重、倒排索引等等各个环节中，都会面对如此海量的数据（比如网页）。所以，利用集群并行处理显然是大势所趋。

一台机器过于低效，那我们就把任务拆分到多台机器上来处理。如果拆分之后的小任务之间互不干扰，独立计算，最后再将结果合并。这不就是分治思想吗？

实际上，MapReduce 框架只是一个任务调度器，底层依赖 GFS 来存储数据，依赖 Borg 管理机器。它从 GFS 中拿数据，交给 Borg 中的机器执行，并且时刻监控机器执行的进度，一旦出现机器宕机、进度卡壳等，就重新从 Borg 中调度一台机器执行。

尽管 MapReduce 的模型非常简单，但是在 Google 内部应用非常广泛。

39 | 回溯算法

回溯算法思想非常简单，但是应用却非常广泛。它除了用来指导像深度优先搜索这种经典的算法设计之外，还可以用在很多实际的软件开发场景中，比如正则表达式匹配、编译原理中的语法分析等。

除此之外，很多经典的数学问题都可以用回溯算法解决，比如：

• 数独
• 八皇后
• 0-1 背包
• 图的着色
• 旅行商问题
• 全排列

回溯算法大部分情况下都是用来解决广义的搜索问题，也就是，从一组可能的解中，选择出一个满足要求的解。回溯算法非常适合用递归来实现，在实现的过程中，剪枝操作是提高回溯效率的一种技巧。

回溯算法本质上就是枚举，适合应用于缺乏规律，或我们还不了解其规律的搜索场景中。

如何理解回溯算法

在我们的一生中，会遇到很多重要的岔路口。在岔路口上，每个选择都会影响我们今后的人生。有的人在每个岔路口都能做出最正确的选择，最后生活、事业都达到了一个很高的高度；而有的人一路选错，最后碌碌无为。如果人生可以量化，那如何才能在岔路口做出最正确的选择，让自己的人生“最优”呢？

我们可以借助前面学过的贪心算法，在每次面对岔路口的时候，都做出看起来最优的选择，期望这一组选择可以使得我们的人生达到“最优”。但是，我们前面也讲过，贪心算法并不一定能得到最优解。那有没有什么办法能得到最优解呢？

2004 年上映了一部非常著名的电影《蝴蝶效应》，讲的就是主人公为了达到自己的目标，一直通过回溯的方法，回到童年，在关键的岔路口，重新做选择。当然，这只是科幻电影，我们的人生是无法倒退的，但是这其中蕴含的思想其实就是回溯算法。

笼统地讲，回溯算法很多时候都应用在“搜索”这类问题上。不过这里说的搜索，并不是狭义的指我们前面讲过的图的搜索算法，而是在一组可能的解中，搜索满足期望的解。

回溯的处理思想，有点类似枚举搜索。我们枚举所有的解，找到满足期望的解。为了有规律地枚举所有可能的解，避免遗漏和重复，我们把问题求解的过程分为多个阶段。每个阶段，我们都会面对一个岔路口，我们先随意选一条路走，当发现这条路走不通的时候（不符合期望的解），就回退到上一个岔路口，另选一种走法继续走。

回溯算法的应用

八皇后问题

有一个 `8x8` 的棋盘，希望往里放 8 个棋子（皇后），满足每个棋子所在的行、列、对角线都不能有另一个棋子。
问题：找到所有满足这种要求的放棋子方式。

下图中第一幅图是满足条件的一种方法，第二幅图是不满足条件的。

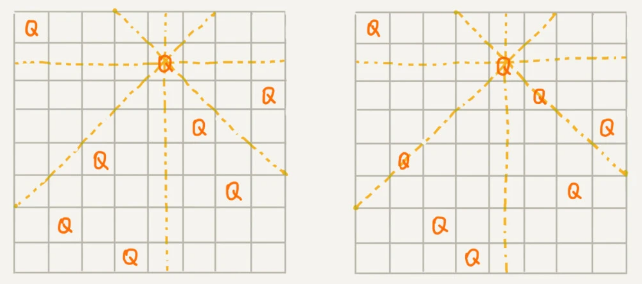
我们把这个问题划分成 8 个阶段，依次将 8 个棋子放到第一行、第二行、第三行……第八行。在放置的过程中，我们不停地检查当前放法，是否满足要求。如果满足，则跳到下一行继续放置棋子；如果不满足，那就再换一种放法，继续尝试。

int[] result = new int[8]; //全局或成员变量，下标表示行，值表示queen存储在哪一列

// 调用方式：cal8queens(0);
public void cal8queens(int row) {
  if (row == 8) { // 8个棋子都放置好了
    printQueens(result);
    return;
  }
  for (int column = 0; column < 8; ++column) { // 每一行都有 8 种放法
    if (isOk(row, column)) {
      result[row] = column; // 第 row 行的棋子放到了 column 列
      cal8queens(row+1); // 递归考察下一行
    }
  }
}

//判断 row 行 column 列放置是否合适
private boolean isOk(int row, int column) {
  int leftup = column - 1; //左上对角线
  int rightup = column + 1; //右上对角线
  for (int i = row-1; i >= 0; --i) { // 逐行往上考察每一行(下面的行还没有放置，所以不需要考察下面的行)
    if (result[i] == column) return false; // 考察【竖线列】：第i行的 column 列有棋子吗？
    if (leftup >= 0) {
      if (result[i] == leftup) return false; // 考察【左上对角线】：第i行的 leftup 列有棋子吗？
    }
    if (rightup < 8) {
      if (result[i] == rightup) return false; // 考察【右上对角线】：第i行的 rightup 列有棋子吗？
    }
    --leftup; ++rightup;
  }
  return true;
}

// 打印出一个二维矩阵
private void printQueens(int[] result) {
  for (int row = 0; row < 8; ++row) {
    for (int column = 0; column < 8; ++column) {
      if (result[row] == column) System.out.print("Q "); //下标表示行，值表示 queen 存储在哪一列
      else System.out.print("* ");
    }
    System.out.println();
  }
  System.out.println();
}

0-1 背包问题

0-1 背包是非常经典的算法问题，很多场景都可以抽象成这个问题模型。这个问题的经典解法是动态规划，不过也可以用回溯法解决。

有 n 个重量不等并且不可分割的物品，现在期望选择几件物品装到背包中，但是选择物品的总重量不能超过背包的承载重量 Wkg。
问题：如何选择物品才可以让背包中物品的总重量最大？

在贪心算法那一节，物品是可以分割的，我们可以装某个物品的一部分到背包里面。但是今天这个背包问题，物品是不可分割的，要么装要么不装，所以叫 0-1 背包问题。显然，这个问题已经无法通过贪心算法来解决了。我们现在来看看，用回溯算法如何来解决。

对于每个物品来说，都有两种选择，装进背包或者不装进背包。对于 n 个物品来说，总的装法就有 2^n 种，去掉总重量超过 Wkg 的，从剩下的装法中选择总重量最接近 Wkg 的。不过，我们如何才能不重复地穷举出这 2^n 种装法呢？

我们可以把物品依次排列，整个问题就分解为了 n 个阶段，每个阶段对应一个物品怎么选择。先对第一个物品进行处理，选择装进去或者不装进去，然后再递归地处理剩下的物品。

public int maxW = 0; // 存储背包中物品总重量的最大值

// i 表示考察到哪个物品了，totalW 表示当前已经装进去的物品的重量和，items 表示每个物品的重量，count 表示物品个数，packageW 表示背包重量
// 假设背包可承受重量100，物品个数10，物品重量存储在数组a中，那可以这样调用函数：findMaxWight(0, 0, a, 10, 100)
public void findMaxWight(int i, int totalW, int[] items, int count, int packageW) {
    if (totalW == packageW || i == count) {  // 递归结束条件：背包刚好装满了，或者已经考察完所有的物品
        if (totalW > maxW) maxW = totalW; // 保证 maxW 跟踪所有选择中的最大值
        return;
    }
    findMaxWight(i + 1, totalW, items, count, packageW); // 当前物品不装进背包，直接考虑下一个，此时 totalW 不更新
    if (totalW + items[i] <= packageW) { // 剪枝：如果已经超过可以背包承受的重量的时候，后面的就不装了
        findMaxWight(i + 1, totalW + items[i], items, count, packageW); // 当前物品装进背包，此时 totalW 更新
    }
}

正则表达式匹配

正则表达式中，最重要的就是通配符，通配符结合在一起，可以表达非常丰富的语义。

假设正则表达式中只包含`*`和`?`这两种通配符，并且规定`*`可匹配任意个任意字符，`?`可匹配零个或者一个任意字符。
问题：如何判断一个给定的文本能否跟给定的正则表达式匹配？

我们依次考察正则表达式中的每个字符

• 如果是普通字符，我们就直接跟文本的字符进行匹配，如果相同，则继续往下处理；如果不同，则回溯。
• 如果是通配符，我们就有多种处理方式了，也就是所谓的岔路口，比如*有多种匹配方案，可以匹配任意个文本串中的字符，我们就先随意的选择一种匹配方案，然后继续考察剩下的字符。如果中途发现无法继续匹配下去了，我们就回到这个岔路口，重新选择一种匹配方案，然后再继续匹配剩下的字符。

public class Pattern {
  private boolean matched = false;
  private char[] pattern; // 正则表达式
  private int plen; // 正则表达式长度

  public Pattern(char[] pattern, int plen) {
    this.pattern = pattern;
    this.plen = plen;
  }

  public boolean match(char[] text, int tlen) { // 文本串及长度
    matched = false;
    rmatch(0, 0, text, tlen);
    return matched;
  }

  private void rmatch(int ti, int pj, char[] text, int tlen) {
    if (matched) return; // 如果已经匹配了，就不要继续递归了
    if (pj == plen) { // 正则表达式到结尾了
      if (ti == tlen) matched = true; // 文本串也到结尾了
      return;
    }

    if (pattern[pj] == '*') { // 通配符 * 可匹配任意个字符
      for (int k = 0; k <= tlen-ti; ++k) {
        rmatch(ti+k, pj+1, text, tlen);
      }
    } else if (pattern[pj] == '?') { // 通配符 ? 可匹配0个或者1个字符
      rmatch(ti, pj+1, text, tlen);
      rmatch(ti+1, pj+1, text, tlen);
    } else if (ti < tlen && pattern[pj] == text[ti]) { // 普通字符，完全匹配才行
      rmatch(ti+1, pj+1, text, tlen);
    }
  }
}

2021-9-25